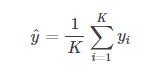摘自 章华燕
思想:对于任意的 n 维输入向量,其对应于特征空间一个点,输出为该特征向量所对应的类别标签或者预测值。
它实际上的工作原理是利用训练数据对特征向量空间进行划分,并将其划分的结果作为其最终的算法模型。
分类算法
KNN 分类算法的分类预测过程十分的简单和容易理解:对于一个需要预测的输入向量 x,我们只需要在训练数据集中寻找 k 个与向量 x 最近的向量的集合,然后把 x 的类标预测为这 k 个样本中类标数最多的那一类。
输入: 训练数据集
T={(x1,y1),(x2,y2),...,(xN,yN)}
其中:xi∈X⊆Rn,为 n 维的实例特征向量。yi∈Y={c1,c2,...,cK}为实例的类别,i=1,2,...,Ni=1,2,...,N,预测实例 xx。
输出: 预测实例 xx 所属类别 yy。
算法执行步骤:
- 根据给定的距离度量方法(一般情况下使用欧氏距离)在训练集 TT 中寻找出与 xx 最相近的 k 个样本点,并将这 k 个样本点所表示的集合记为 Nk(x);
- 根据如下所示的多数投票的原则确定实例 x 所属类别 y:
式(5.1)中 II 为指示函数:
从上述的 KNN 算法原理的讲解中,我们会发现有两个因素必须确定才能使 KNN 分类算法真正能够运行:
(1)算法超参数 K;
(2)模型向量空间的距离度量。
k 值的确定

距离度量
样本空间中两个点之间的距离度量表示的是两个样本点之间的相似程度:距离越短,表示相似程度越高;相反,距离越大,表示两个样本的相似程度低。
常用的距离度量方式有:
- 闵可夫斯基距离;
- 欧氏距离;
- 曼哈顿距离;
- 切比雪夫距离;
- 余弦距离。
KD树
当特征空间维度特别高或者样本容量大时,暴力计算k近邻 就会非常耗时,该方法并不可行。
就会非常耗时,该方法并不可行。
为了快速查找到 K 近邻,考虑使用特殊的数据结构存储训练数据,用来减少搜索次数。其中,KDTree 就是最著名的一种。
KD 树(K-dimension Tree)是一种对 K 维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。KD 树是是一种二叉树,表示对 K 维空间的一个划分,构造 KD 树相当于不断地用垂直于坐标轴的超平面将 K 维空间切分,构成一系列的 K 维超矩形区域。KD 树的每个结点对应于一个 K 维超矩形区域。利用 KD 树可以省去对大部分数据点的搜索,从而减少搜索的计算量。
KD 树的构造
KD 树的构造是一个递归的方法:
(1)构造根节点,使根节点对应于 K 维空间中包含的所有点的超矩形区域;
(2)不断地对 K 维空间进行切分,生成子节点。

回归算法
对新来的预测实例寻找 K 近邻,然后对这 K 个样本的目标值去均值即可作为新样本的预测值: