聚类算法——DBSCAN算法原理及公式

聚类的定义

聚类就是对大量未知标注的数据集，按数据的内在相似性将数据集划分为多个类别，使类别内的数据相似度较大而类别间的数据相似度较小。聚类算法是无监督的算法。

常见的相似度计算方法

闵可夫斯基距离Minkowski/欧式距离

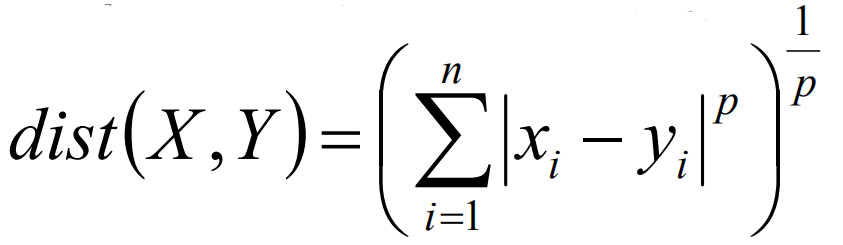
在上述的计算中，当p=1时，则是计算绝对值距离，通常叫做曼哈顿距离，当p=2时，表述的是欧式距离。

杰卡德相似系数(Jaccard)

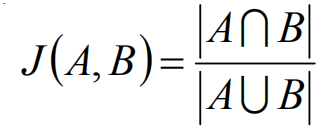
杰卡德相关系数主要用于描述集合之间的相似度，在目标检测中，iou的计算就和此公式相类似

余弦相似度

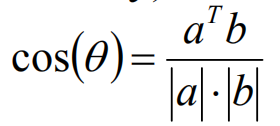
 余弦相似度通过夹角的余弦来描述相似性

Pearson相似系数

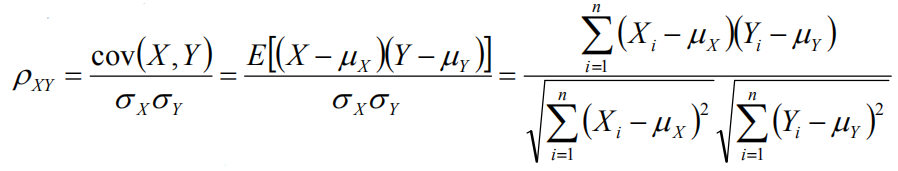
相对熵(K-L距离)

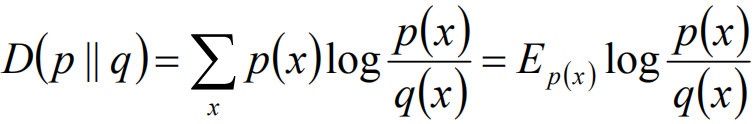
相对熵的相似度是不对称的相似度，D(p||q)不一定等于D(q||p)。

聚类的基本思想

给定一个有N个对象的数据集，划分聚类的技术将构造数据的K个划分，每个划分代表一个簇，K<=n。也就是说，聚类将数据划分为k个簇，而且这k个划分满足下列条件：

每个簇至少包含一个对象，每一个对象属于且仅属于一个簇。

具体的步骤为，对于给定的k，算法首先给出一个初始的划分方法。以后通过反复迭代的方法改变划分，使得每一次改进之后的划分方案都较前一次更好。

密度聚类

密度聚类方法的指导思想是，只要一个区域中的点的密度大于某个阈值，就把它加到与之相近的聚类中去。这类算法能够克服基于距离的算法只能发现“类圆形”的聚类的缺点，可以发现任意形状的聚类，且对噪声数据不敏感。但计算密度单元的计算复杂度大，需要建立空间索引来降低计算量。

DBSCAN算法

DBSCAN是一个比较有代表性的基于密度聚类的聚类算法，它对簇的定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在有噪声的数据中发现任意形状的聚类。

DBSCAN相关定义

对象的ε-邻域：给定对象在半径ε内的区域。

核心对象：对于给定的数据m，如果一个对象的ε-邻域至少包含有m个对象，则成为该对象的核心对象。

直接密度可达：给定一个对象集合D，如果p是在q的ε-邻域内，而q是一个核心对象，则对象p从对象q出发是直接密度可达的。

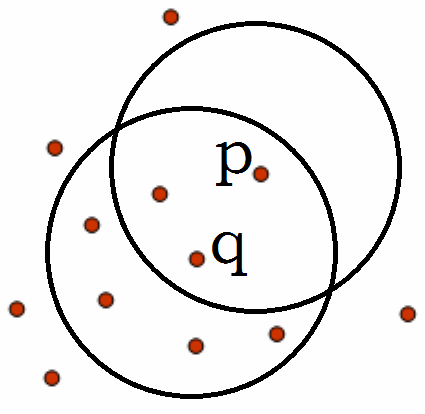
密度可达：如果存在一个对象链p1p2···pn，p1=q，pn=p，对pi属于D，pi+1是从pi关于ε和m直接密度可达的，则对象p是从对象q关于ε和m密度可达的。

密度相连：如果对象集合D中存在一个对象o，使得对象p和q是从o关于ε和m密度可达的，那么对象p和q是关于ε和m密度相连的。

簇：一个基于密度的簇是最大的密度相连对象的集合。

噪声：不包含在任何簇中的对象称为噪声。

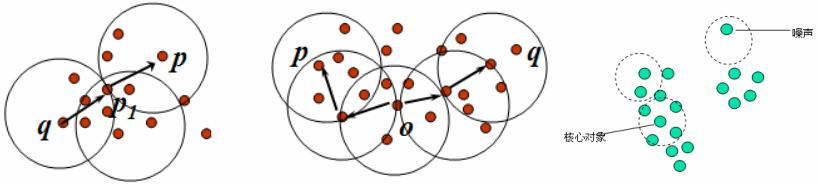
DBSCAN通过检查数据集中的每个对象的ε-邻域来寻找聚类，如果一个点p的ε-邻域包含对于m个对象，则创建一个p作为核心对象的新簇。然后，DBSCAN反复地寻找这些核心对象直接密度可达的对象，这个过程可能涉及密度可达簇的合并。当没有新的点可以被添加到任何簇时，该过程结束。算法的中ε和m是根据先验知识来给出的。