在机器学习中,我们构建的模型,大部分都是通过求解代价函数的最优值进而得到模型参数的值。那么,对于构建好的目标函数和约束条件,我们应该如何对其进行求解呢!
在机器学习中,最常用的优化方法是梯度下降法。梯度下降法或最速下降法是求解无约束最优化问题的一种最常用的方法,有实现简单的优点。梯度下降法是迭代算法,每一步需要求解目标函数的梯度向量。
假设f(x)是Rn上具有一阶连续偏导数的函数。要求解的无约束最优化问题是:
![]()
x*表示目标函数f(x)的极小值。
梯度下降法是一种迭代算法。选取适当的初值x0,不断迭代,更新x的值,进行目标函数的极小化,直到收敛。由于负梯度方向是使函数值下降最快的反向,在迭代的每一步,以负梯度方向更新x的值,从而达到减小函数值的目的。
由于f(x)是具有一阶连续偏导数,若第k次迭代值为X(k),则可将f(x)在X(k)附近进行一阶泰勒展开:

这里,![]() 为f(x)在X(k)的梯度。
为f(x)在X(k)的梯度。
求出第k+1次迭代值X(k+1):
![]()
其中,P(k)是搜索方向,取负梯度方向![]() ,
,![]() 是步长,由一维搜索确定,即
是步长,由一维搜索确定,即![]() 使得:
使得:
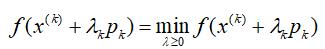

当目标函数是凸函数时,梯度下降的解是全局最优解,一般情况下,其解不保证是全局最优解。梯度下降法的收敛速度也未必是很快的。
梯度下降算法根据更新梯度所使用的样本数,又可以分为:标准梯度下降,随机梯度下降,批量梯度下降。
标准梯度下降:通过所有的训练样本来进行梯度下降,每一次得到的结果都能靠近极值点,但是对于所有的样本进行计算,每次更新需花费的时间较多。
随机梯度下降:通过每次随机选取一个样本来对参数进行更新,由于是随机选取一个样本来进行更新,因而并不是每次迭代都能够靠近极值点,但是迭代的整体方向是朝着最优化方向的,并且迭代的速度较快。
批量梯度下降:将上述两种方法进行折中,就得到了批量梯度下降,将训练数据分为若干个批次,每次选取其中的一个批次进行迭代,既能够加快训练速度,又能够使得模型稳定的收敛。
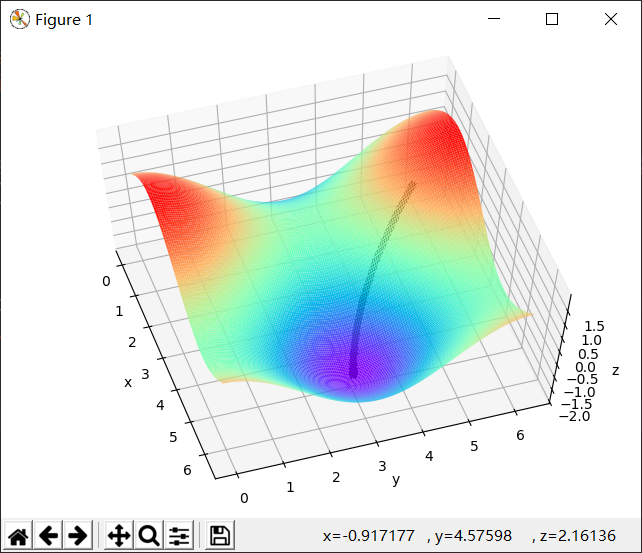
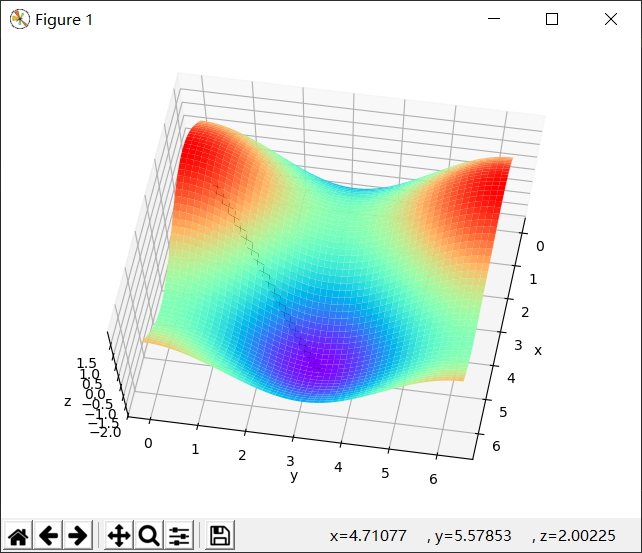
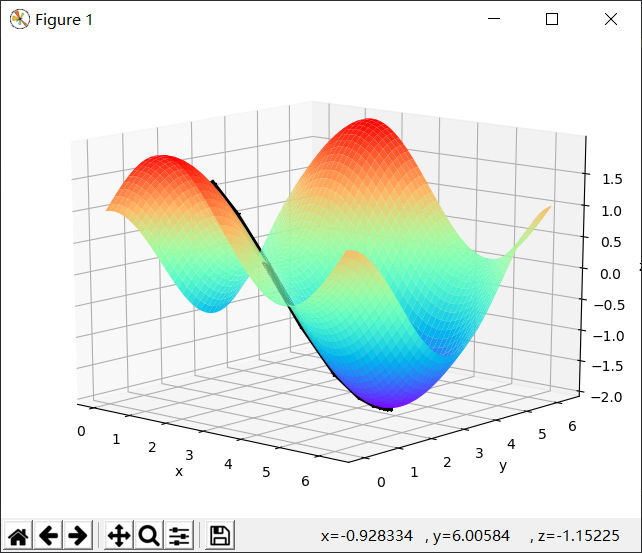
简单代码演示:
1 import numpy as np 2 import matplotlib as mpl 3 import matplotlib.pyplot as plt 4 from mpl_toolkits.mplot3d import Axes3D 5 6 def f(x, y): 7 # z = 2*np.sin(1.5*x**2 - 0.25*y + 0.25*np.pi) + 3*np.cos(1.5*x*y - 0.5*np.pi) 8 z = np.sin(x) + np.cos(y) 9 return z 10 11 if __name__ == '__main__': 12 t = np.linspace(0, np.pi*2, 50) 13 x1, y1 = np.meshgrid(t, t) 14 z = np.stack([x1.flat, y1.flat], axis=1) 15 # print(z.shape) 16 x = z[:, 0] 17 y = z[:, 1] 18 # print(x) 19 z = f(x, y) 20 # print(z) 21 z = z.reshape(x1.shape) 22 # print(z.shape) 23 fig = plt.figure() 24 ax = Axes3D(fig) 25 ax.plot_surface(x1, y1, z, rstride=1, cstride=1, cmap='rainbow') 26 plt.xlabel("x") 27 plt.ylabel("y") 28 ax.set_zlabel("z") 29 30 x0 = 2 31 y0 = 0.5 32 n = 0.5 33 xy = [] 34 for i in range(100): 35 xn = x0 - n*np.cos(x0) 36 yn = y0 + n*np.sin(y0) 37 x0 = xn 38 y0 = yn 39 xy.append([x0, y0]) 40 xy = np.array(xy) 41 ax.plot(xy[:, 0], xy[:, 1], f(xy[:, 0], xy[:, 1]), 'k-' ,linewidth=5) 42 ax.plot(xy[:, 0], xy[:, 1], f(xy[:, 0], xy[:, 1]), 'k*' ,linewidth=20) 43 plt.show()