leetcode每日一题（2020-06-18）：1028. 从先序遍历还原二叉树

题目描述：
我们从二叉树的根节点 root 开始进行深度优先搜索。
在遍历中的每个节点处，我们输出 D 条短划线（其中 D 是该节点的深度），然后输出该节点的值。（如果节点的深度为 D，则其直接子节点的深度为 D + 1。根节点的深度为 0）。
如果节点只有一个子节点，那么保证该子节点为左子节点。
给出遍历输出 S，还原树并返回其根节点 root。



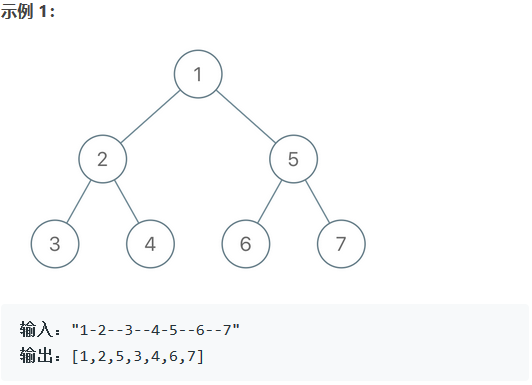
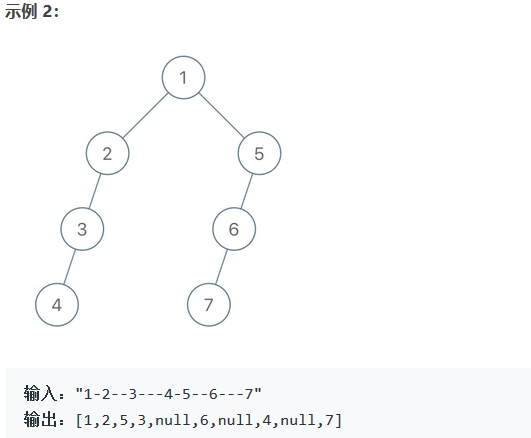
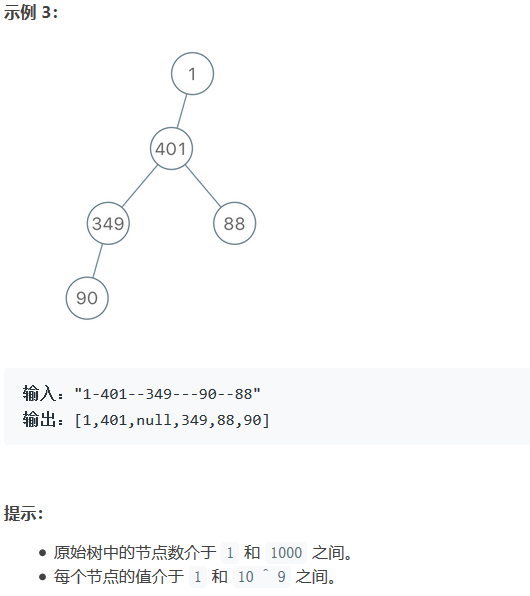
今日学习：
1.复习map
2.巩固树的相关知识


先说思路：
1.我本来看到输出是层序遍历的样子，就想着用hashmap来存，key存深度，value存节点数值
2.我忽略了hashmap键值唯一的特性，存完之后发现不对，改用数组来存value
3.我对树结构理解的相当不透彻，导致存完map我就蒙了不知道该怎么写了，因为我发现我这样存的话不同的树可能是同一个map
4.看题解，发现根本和我的方法不一样，是用栈来做的，copy一番
5.后来想想，hashmap中，如果下一层的数在前序遍历中是不挨着的，就说明左边有子树，如果是挨着的就说明左子树为null，然后又因为我自己存的value是数组，我又蒙了不知道怎么算了
6.看到一个小伙伴用deeps[]和nodes[]两个数组来存前序遍历的节点以及深度，恍然大悟，我想要的不就是深度么，和是不是层序遍历关系不大，果断学习一波
7.最后还看到可以用递归：1-2--3--4-5--6--7可以找到短线数目相同的，分成2--3--4和5--6--7，继续分成3和4、6和7...


题解1：官方栈解法

const recoverFromPreorder = (S) => {
  const stack = []
  for (let i = 0; i < S.length;) {
    let curLevel = 0 //一个curNode对应一个curLevel
    while (i < S.length && S[i] == '-') { // 避免循环半途中出界
      i++
      curLevel++    // 连字符个数代表level
    }
    const start = i // 记录当前节点值的开始位置
    while (i < S.length && S[i] != '-') {
      i++           // 指针移到当前节点值的结束位置
    }
    const curNode = new TreeNode(S.slice(start, i)) //创建当前节点
    if (stack.length == 0) { // ROOT入栈，不用找父亲，continue
      stack.push(curNode)
      continue
    }
    while (stack.length > curLevel) { // 栈顶不是父亲，栈顶出栈
      stack.pop()                     // 直到栈顶是父亲
    }
    if (stack[stack.length - 1].left) {       // 左儿子已存在
      stack[stack.length - 1].right = curNode // 安排为右儿子
    } else {
      stack[stack.length - 1].left = curNode  // 安排为左儿子
    }
    stack.push(curNode) // 节点肯定要入栈一次
  }
  return stack[0]       // 栈底就是根节点
};

题解2：双数组解法

var recoverFromPreorder = function(S) {
    //用来存层序遍历的节点数组
    let nodes = []
    //用来存节点的树结构
    let node
    //用来存层序遍历的节点深度
    let deeps = []
    //用来计算'-'的个数，即节点深度
    let deep = 0
    //用来存节点数字
    let s = ''
    for(let i = 0; i < S.length; i++) {
        if(S[i] != '-') {
            //是数字，存起来
            s += S[i]
            //判断下一位是不是数字，是就继续存，不是就生成节点树结构
            if(S[i + 1] == '-' || i == S.length - 1) {
                node = new TreeNode(s)
                deeps.push(deep)
                nodes.push(node)
                //准备存下一个节点
                deep = 0
                s = ''
            }
        }else {
            //不是数字，深度+1
            deep++
        }
    }
    for(let i = 1; i < nodes.length; i++) {
        if(deeps[i] == deeps[i - 1]) {
            //和前一个节点深度相同，则表示它两是兄弟，找到父亲认亲为右儿子（左儿子已经是i - 1了）
            nodes[i - 2].right = nodes[i]
        }else if(deeps[i] > deeps[i - 1]) {
            //大于前一个节点深度，则表示它是前一个节点的左儿子
            nodes[i - 1].left = nodes[i]
        }else {
            //小于前一个深度，则表示它是前一个节点的叔父，需要找到它们的爷爷
            let temp = i
            while(deeps[i] <= deeps[temp]) {
                temp--
            }
            //找到爷爷之后，将叔父认亲为右儿子
            nodes[temp].right = nodes[i]
        }
    }
    return nodes[0]
}