leetcode每日一题（2020-05-09）：69.x的平方根

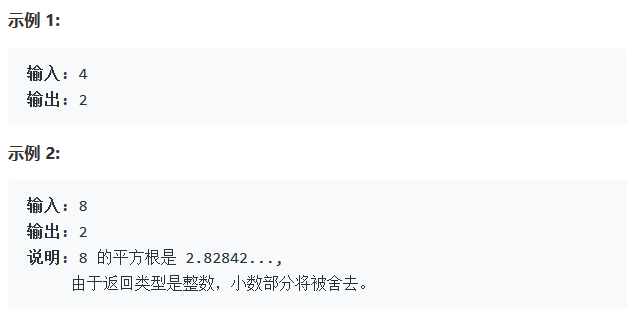
题目描述:实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

今日学习：
1.复习二分法
2.加一个感悟 同样是二分法 细节是魔鬼

题解1：首先肯定是自带的函数

var mySqrt = function(x) {
      return Math.floor(Math.sqrt(x));
}

题解2：我自己想的二分法，因为大于4的x其实只需要将end设置为Math.ceil(x/2)就可以了，我觉得可以节省时间，【写博客的时候想到，这不过是少了一次二分而已，一一好像不是很大】

var mySqrt = function(x) {
      if(x == 0 || x < 1){return 0;}
      if(x >= 1 && x < 4){return 1;}
      if(x == 4){return 2;}
      else{
            var start = 0;
            var end = Math.ceil(x / 2);
            var mid = (start + end) >> 1;
            while(start != end - 1){
                  if(mid * mid == x){return mid;}
                  if(mid * mid > x){
                        end = mid;
                        mid = (start + end) >> 1;
                  }else{
                        start = mid;
                        mid = (start + end) >> 1;
                  }
           }
      }
      return start;
};

题解3：别人的二分法，这样可以减少查找次数（真实的减少hhh，因为判断条件的缘故不用执行那么多循环次数）

//参考别人的二分法
var mySqrt = function(x) {
    if(x === 0) return 0;
    var start = 0, end = x;
    var i = (start + end) >> 1;
    while(i < x){
       i = (start + end) >> 1;
        if(i * i === x) return i;
        if(start === end - 1) break;
        if(i * i > x) end = i;
        else start = i;
    }
    if(start * start <= x && end * end > x) return start;
    return end;
};

题解4:2和3结合：

//结合到一起的二分法
var mySqrt = function(x) {
    if(x == 0 || x < 1){return 0;}
    if(x >= 1 && x < 4){return 1;}
    if(x == 4){return 2;}
    var start = 0, end = Math.ceil(x / 2);
    var mid = (start + end) >> 1;
    while(mid < Math.ceil(x / 2)){
        mid = (start + end) >> 1;
        if(mid * mid === x) return mid;
        if(start === end - 1) break;
        if(mid * mid > x) end = mid;
        else start = mid;
    }
    if(start * start <= x && end * end > x) return start;
    return end;
};

题解5：

var mySqrt = function(x) {
    if(x == 0 || x ==1){
        return x;
    }
    var left = 1;
    var right = x;
    while(left <= right){
       var middle = left + ((right-left)>>1);
       if(middle*middle == x){
           return middle;
       }else if(middle*middle > x){
           right = middle-1;
       }else{
           left = middle+1;
       }
    }
    return right;
};

题解6：

var mySqrt = function(x) {
    if(x == 0 || x < 1){return 0;}
    if(x >= 1 && x < 4){return 1;}
    if(x == 4){return 2;}
    else{
        var start = 2;
        var end = Math.ceil(x / 2);
        while(start <= end){
            var mid = (start + end) >> 1;
            if(mid * mid == x){return mid;}
            if(mid * mid > x){
                end = mid - 1;
            }else{
                start = mid + 1;
            }
        }
    }
    return end;
};