平面上n个点,两个人交替决策,用线段连接两个点,但不能跨越其他点或者已经存在的线段。不能做的人算输,问你谁赢。
实际上,跟两个人的决策无关,n个点将平面三角剖分,只需要算出有几条边即可。
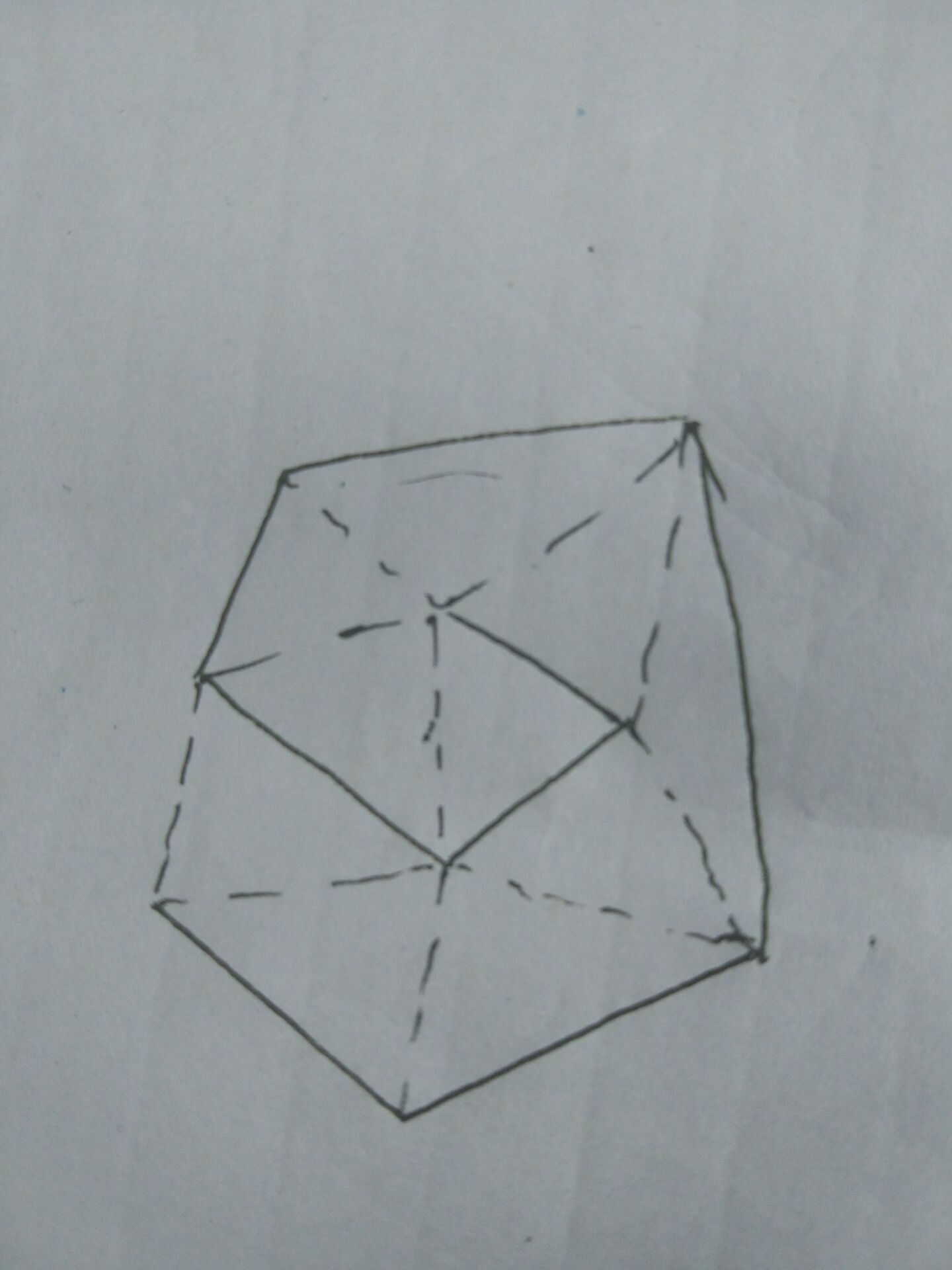
凸包上如果有K个点,那么图中那K-1条实边每条贡献一个三角形。
凸包内其他的边,每条贡献2个三角形。除了最中心那一个贡献一个。
假设总的三角形数是X,那么总的线段数就是(X*3+K)/2。
线段数是奇数就先手胜,否则后手胜。
#include<cstdio>
#include<algorithm>
using namespace std;
struct Point{
int x,y;
Point(const int &x,const int &y){
this->x=x;
this->y=y;
}
Point(){}
void read(){
scanf("%d%d",&x,&y);
}
}p[1005],q[1005];
typedef Point Vector;
Vector operator - (const Point &a,const Point &b){
return Vector(a.x-b.x,a.y-b.y);
}
int Cross(const Vector &a,const Vector &b){
return a.x*b.y-a.y*b.x;
}
bool cmp(const Point &a,const Point &b){
return a.x!=b.x ? a.x<b.x : a.y<b.y;
}
int n,K,T;
int main(){
// freopen("d.in","r",stdin);
scanf("%d",&T);
for(;T;--T){
K=0;
scanf("%d",&n);
for(int i=0;i<n;++i){
p[i].read();
}
sort(p,p+n,cmp);
bool flag=1;
for(int i=1;i<n-1;++i){
if(Cross(p[i+1]-p[i],p[i]-p[i-1])!=0){
flag=0;
break;
}
}
if(flag){
puts((n-1)%2==1 ? "T^T" : "OwO");
continue;
}
for(int i=0;i<n;++i){
while(K>1 && Cross(q[K-1]-q[K-2],p[i]-q[K-1])<0){
--K;
}
q[K++]=p[i];
}
for(int i=n-2,t=K;i>=0;--i){
while(K>t && Cross(q[K-1]-q[K-2],p[i]-q[K-1])<0){
--K;
}
q[K++]=p[i];
}
--K;
int A=K-1;
int B=n-K-1;
int sjxs=A+B*2+1;
puts((sjxs*3+K)/2%2==1 ? "T^T" : "OwO");
}
return 0;
}