• 浅谈线段树

    title: 线段树-学习
    date: 2019-08-02 10:03:56
    tags: NULL

    前言：线段树是一种二叉搜索树，能通关TA实现修改、区间查询等功能……
    （ 相信大家都懂的……）

    好吧，在这里，我们就来介绍线段树的单点修改、区间修改以及区间查询的方法。

    单点修改，区间查询

    Emmmmmm 这算是学习线段树的第一步了吧……

    _为什么要用线段树去干这件事情呢？
    你会发现，如果你直接暴力去查询一个区间 [l,r] 的和，那么这样做的时间复杂度将会使O(n)的；但是，如果你用线段树去实现这一过程，那么时间复杂度将会降成O(log n)。 _

    接下来我们就来讲算法的原理。

    既然线段树被称为“树”，自然是一种树状的数据结构。它的每一个节点都储存了某一个区间的信息。
    它的结构如图所示：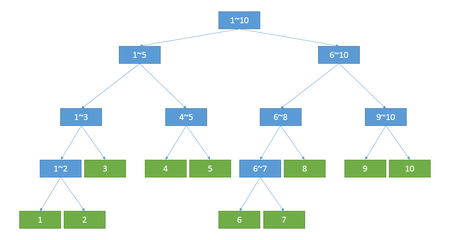
    by _皎月半洒花

    进行修改时，我们需要更新指定修改节点已经所以与其相关的区间（即包含此节点的所有区间），查询时需查询的区间的值可以有其内部的几个区间的值拼起来得到。
    代码实现：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    #include<iostream>
    #include<algorithm>
    #include<cstring>
    #include<malloc.h>
    #include<cstdio>

    using namespace std;

    struct tree{
        int sum;
        tree *lson,*rson;
    }*root=(tree*)malloc(sizeof(tree));

    int n,x,y,s,m;

    void built(tree *tre,int l,int r)
    {
        if(l==r) 
        {
            scanf("%d",&x);
            tre -> sum = x;
            return ;
        }
        tree *left=(tree*)malloc(sizeof(tree));
        tree *right=(tree*)malloc(sizeof(tree));
        tre -> lson=left;
        tre -> rson=right;
        int mid=(l+r)>>1;
        built(tre -> lson,l,mid);
        built(tre -> rson,mid+1,r);
        tre -> sum=tre -> lson -> sum + tre -> rson -> sum;
    }

    void change(tree *tre,int a,int x,int l,int r)
    {
        if(x==l&&x==r)
        {
            tre -> sum+=a;
            return ;
        }
        tre -> sum += a;
        int mid=(l+r)>>1;
        if(x<=mid) change(tre -> lson,a,x,l,mid);
        if(x>mid) change(tre -> rson,a,x,mid+1,r);
    }

    int query(tree *tre,int l,int r,int x,int y)
    {
        if(x<=l&&y>=r) return tre -> sum;
        int mid=(l+r)>>1,ans1=0,ans2=0;
        if(x<=mid) ans1=query(tre -> lson,l,mid,x,y);
        if(y>mid) ans2=query(tre -> rson,mid+1,r,x,y);
        return ans1+ans2;
    }

    int main()
    {
        scanf("%d%d",&n,&m);
        built(root,1,n);
        for(int i=1;i<=m;i++)
        {
            scanf("%d%d%d",&s,&x,&y);
            if(s==1) change(root,y,x,1,n);
            if(s==2) printf("%d
",query(root,1,n,x,y));
        }
        return 0;
    }
    // PS:我的线段树是用指针写的，如果不喜欢指针可以用数组去实现，节点N的左孩子的下标为2N，右孩子的下标为2N+1。

    想做模板题请戳这里
    （请忽略题目名字，并不是我弄错了，一个模板题的潜力是无穷的）

    区间修改，区间查询

    其实区间修改与单点修改之间只差了一个lazy标记……

    如果你用多次的单点修改来完成区间修改，那么复杂度将会是O（nlogn），显然还不如你直接修改一个数组快qwq……
    所以在这个紧急关头，你需要一个lazy标记去拯救你。
    对于每次区间修改，我们还是从根节点开始找每一个区间，若当前区间[l,r]被需要修改的区间[x,y]完全包含，那么在更新此区间的值的同时，我们还要更新lazy标记，表示该节点的两个子节点需要进行一个大小为lazy的值的修改，但是现在还没有进行。当你打完lazy标记以后，在此次修改中，你就不必再去观该节点的子树了。
    那么，既然我们打了lazy标记，那么以后肯定还是需要让它起作用的。我们在每次修改和查询过程中，若遍历到某点时，该点的lazy标记不为0，则把标记下放（即根据该节点的lazy标记值去修改其子节点的值，并把该节点的lazy加到其子节点的lazy上。注意，lazy的是加过去，而不是直接覆盖！在标记下放完以后，不要忘了把该节点的lazy标记清空）。
    附一下代码：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    91
    92
    93
    94
    95
    96
    97
    #include<iostream>
    #include<cstring>
    #include<cstdio>
    #include<algorithm>

    using namespace std;

    struct tree{
    	long long sum,lazy;
    	tree *lson,*rson;
    	tree()
    	{
    		lazy = 0;
    	}
    };

    long long x,y,k,n,m,s;

    void built(tree *tre,int l,int r)
    {
    	tre -> lazy = 0;
    	if(l == r)
    	{
    		scanf("%d",&x);
    		tre -> sum = x;
    		return ;
    	}
    	int mid = (l + r) >> 1;
    	tree *son1 =(tree*) malloc (sizeof(tree));
    	tree *son2 =(tree*) malloc (sizeof(tree));
    	tre -> lson = son1;
    	tre -> rson = son2;
    	built(tre -> lson,l,mid);
    	built(tre -> rson,mid + 1,r);
    	tre -> sum = tre -> lson -> sum + tre -> rson -> sum;
    }
    void pushdown(tree *tre,int l,int r)
    {
    	if(l != r)
    	{
    		int mid = (l + r) >> 1;
    		tre -> lson -> lazy = tre -> lson -> lazy + tre -> lazy;
    		tre -> lson -> sum = tre -> lson -> sum + tre -> lazy * (mid - l + 1);
    		tre -> rson -> lazy = tre -> rson -> lazy + tre -> lazy;
    		tre -> rson -> sum = tre -> rson -> sum + tre -> lazy * (r - mid);
    	}
    	tre -> lazy = 0;
    }
    void change(tree *tre,int l,int r,int x,int y,int k)
    {
    	if(l >= x && r <= y)
    	{
    		tre -> lazy += k;
    		tre -> sum = tre -> sum + k * (r - l + 1);
    		return ;
    	}
    	pushdown(tre,l,r);
    	int mid = (l + r) >> 1;
    	if(x <= mid) change(tre -> lson,l,mid,x,y,k);
    	if(y > mid) change(tre -> rson,mid + 1,r,x,y,k);
        tre -> sum = tre -> lson -> sum + tre -> rson ->sum;
    }



    long long query(tree *tre,int l,int r,int x,int y)
    {
    	if(l >= x && r <= y) return tre -> sum;
    	pushdown(tre,l,r);
    	int mid = (l + r) >> 1;
    	long long  t1 = 0,t2 = 0;
    	if(x <= mid) t1 = query(tre -> lson,l,mid,x,y);
    	if(y > mid) t2 = query(tre -> rson,mid + 1,r,x,y);
    	return t1 + t2;
    }

    int main()
    {
    	scanf("%lld%lld",&n,&m);
    	tree *root = (tree*) malloc (sizeof(tree));
    	built(root,1,n);
    	for(int i = 1;i <= m; i++)
    	{
    		scanf("%lld%lld%lld",&s,&x,&y);
    		if(s == 1)
    		{
    			scanf("%lld",&k);
    			change(root,1,n,x,y,k);
    		}
    		else
    		{
    			long long  ans = query(root,1,n,x,y);
    			printf("%lld
",ans);
    		}
    	}
    	return 0;
    }

    想做模板题请戳这里

    线段树除了求和还能干好多事情（如维护区间最大值等），可以自行YY一下下……
  • 相关阅读:
    嵌入式实验一：LED灯点亮
    [转] sql中的in与not in,exists与not exists的区别
    订单管理系统基本情况
    solaris系统分区及格式化
    百度超大网盘邀请码，点击可以获得额外的300M哦
    vb设置代理ip
    我看到一种防伪查询系统，叫做西门防伪防伪查询系统，不知道好不好用。
    零碎知识点整理
    初学WCF之消息模式3——双工模式
    HTTP 错误 500.21 Internal Server Error
  • 原文地址：https://www.cnblogs.com/aurorapolaris/p/13502541.html
Copyright © 2020-2023  润新知