
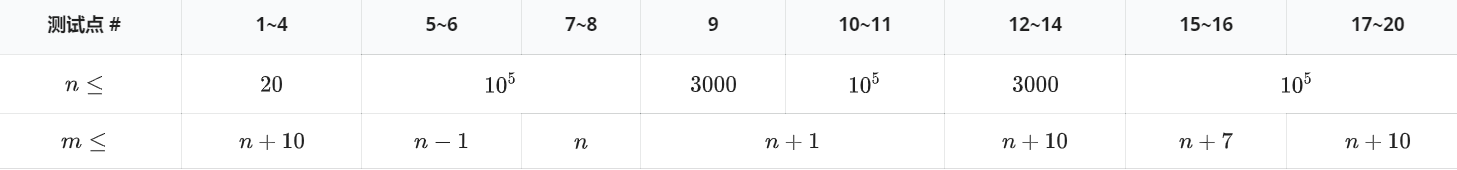
思路历程
1-4 20pts (2^nn)枚举
5-6 10pts (f[i][0/1])
7-8 10pts 基环树 总数-强制选多出来的那条边的两点
9-14 30pts (2^{m-n+1})枚举多出来的边容斥
100pts 虚树
SOL
对多出来的边的点建立虚树
其实不用容斥,每次强制每条边上的点是否选(都是合法状态),加起来就是ans
(k[v][0/1][0/1])表示v转移到虚树上的fa,v、fa选不选是转移系数,预处理出来就OK(简单的树形DP)
注意本题的大多数DP合并两个子节点是(prod)
时间复杂度(O(s2^s),s=n-m+1)
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x=0,f=1;char c=getchar();
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
return f==1?x:-x;
}
const int N=1e5+4,mod=998244353;
vector<int>e[N],t[N];
#define pb push_back
#define ll long long
int n,m,tim,cu,ans;
int mark[N],dfn[N],vis[N],uu[40],vv[40],sz[N];
int g[N][2],k[N][2][2],h[N][2][2],f[N][2],li[N][2];
void xsdfs(int x,int fa){
dfn[x]=++tim;
for(auto v:e[x]){
if(v==fa)continue;
if(!dfn[v]){
xsdfs(v,x);
sz[x]+=sz[v];
continue;
}
mark[x]=1;
if(dfn[x]<dfn[v]){
uu[++cu]=x;
vv[cu]=v;
}
}
mark[x]|=(sz[x]>=2);
sz[x]=sz[x]||mark[x];
}
int predfs(int x){
vis[x]=1;
g[x][0]=g[x][1]=1;
int las,pos=0;
for(auto v:e[x]){
if(vis[v])continue;
las=predfs(v);
if(!las){
g[x][1]=(ll)g[x][1]*g[v][0]%mod;
g[x][0]=(ll)g[x][0]*(g[v][0]+g[v][1])%mod;
}
else if(mark[x]){
t[x].pb(las);
k[las][0][0]=(h[v][1][0]+h[v][0][0])%mod;
k[las][0][1]=(h[v][1][1]+h[v][0][1])%mod;
k[las][1][0]=h[v][0][0];
k[las][1][1]=h[v][0][1];
}
else{
h[x][0][0]=(h[v][1][0]+h[v][0][0])%mod;
h[x][0][1]=(h[v][1][1]+h[v][0][1])%mod;
h[x][1][0]=h[v][0][0];
h[x][1][1]=h[v][0][1];
pos=las;
}
}
if(mark[x]){
h[x][0][0]=h[x][1][1]=1;
h[x][0][1]=h[x][1][0]=0;
pos=x;
}
else{
h[x][0][0]=(ll)h[x][0][0]*g[x][0]%mod;
h[x][0][1]=(ll)h[x][0][1]*g[x][0]%mod;
h[x][1][0]=(ll)h[x][1][0]*g[x][1]%mod;
h[x][1][1]=(ll)h[x][1][1]*g[x][1]%mod;
}
return pos;
}
void dpdfs(int x){
f[x][0]=li[x][1]?0:g[x][0];
f[x][1]=li[x][0]?0:g[x][1];
for(auto v:t[x]){
dpdfs(v);
f[x][0]=((ll)f[v][0]*k[v][0][0]+(ll)f[v][1]*k[v][0][1])%mod*f[x][0]%mod;
f[x][1]=((ll)f[v][0]*k[v][1][0]+(ll)f[v][1]*k[v][1][1])%mod*f[x][1]%mod;
}
}
int main(){
n=read();m=read();
for(int i=1,u,v;i<=m;i++){
u=read();v=read();
e[u].pb(v);e[v].pb(u);
}
xsdfs(1,0);mark[1]=1;
predfs(1);
for(int s=0,S=(1<<m-n+1);s<S;s++){
for(int i=1;i<=m-n+1;i++)
if((s>>i-1)&1)li[uu[i]][1]=li[vv[i]][0]=1;
else li[uu[i]][0]=1;
dpdfs(1);
ans=((ll)ans+f[1][1]+f[1][0])%mod;
for(int i=1;i<=m-n+1;i++)
if((s>>i-1)&1)li[uu[i]][1]=li[vv[i]][0]=0;
else li[uu[i]][0]=0;
}
cout<<ans;
return (0-0);
}