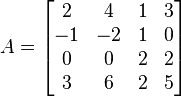【原创】开源Math.NET基础数学类库使用(16)C#计算矩阵秩

               本博客所有文章分类的总目录：【总目录】本博客博文总目录-实时更新 

开源Math.NET基础数学类库使用总目录：【目录】开源Math.NET基础数学类库使用总目录

　　上个月对Math.NET的基本使用进行了介绍，主要内容有矩阵，向量的相关操作，解析数据格式，数值积分，数据统计，相关函数，求解线性方程组以及随机数发生器的相关内容。这个月接着深入发掘Math.NET的各种功能，并对源代码进行分析，使得大家可以尽可能的使用Math.NET在.NET平台下轻易的开发数学计算相关的，或者可以将其中的源码快速移植到自己的系统中去(有时候并不需要所有的功能，只需要其中的部分功能代码)，今天要介绍的是Math.NET中利用C#计算矩阵秩的功能。

　　本文原文地址：http://www.cnblogs.com/asxinyu/p/4304304.html

1.什么是矩阵秩

　　矩阵的秩是反映矩阵固有特性的一个重要概念。在线性代数中，一个矩阵A的列秩是A的线性无关的纵列的极大数目。类似地，行秩是A的线性无关的横行的极大数目。矩阵的列秩和行秩总是相等的，因此它们可以简单地称作矩阵A的秩。通常表示为r(A)，rk(A)或rank A。矩阵的行秩与列秩相等，是线性代数基本定理的重要组成部分. 其基本证明思路是，矩阵可以看作线性映射的变换矩阵，列秩为像空间的维度，行秩为非零原像空间的维度，因此列秩与行秩相等，即像空间的维度与非零原像空间的维度相等（这里的非零原像空间是指约去了零空间后的商空间：原像空间）。这从矩阵的奇异值分解就可以看出来。矩阵秩的计算最容易的方式是高斯消去法，这里引用维基百科的内容：

　　计算矩阵A的秩的最容易的方式是高斯消去法，即利用矩阵的初等变换生成一个行阶梯型矩阵，由于矩阵的初等变换不改变矩阵的秩，因此A的行梯阵形式有同A一样的秩。经过初等变换的矩阵的非零行的数目就是原矩阵的秩。例如考虑4 × 4矩阵：

我们看到第2纵列是第1纵列的两倍，而第4纵列等于第1和第3纵列的总和。第1和第3纵列是线性无关的，所以A的秩是2。这可以用高斯算法验证。它生成下列A的行梯阵形式:

　　它有两个非零的横行。在应用在计算机上的浮点数的时候，基本高斯消去（LU分解）可能是不稳定的，应当使用秩启示（revealing）分解。一个有效的替代者是奇异值分解（SVD），但还有更少代价的选择，比如有支点（pivoting）的QR分解，它也比高斯消去在数值上更强壮。秩的数值判定要求对一个值比如来自SVD的一个奇异值是否为零的依据，实际选择依赖于矩阵和应用二者。

http://zh.wikipedia.org/wiki/秩_(线性代数)

　　矩阵秩在线性代数中的应用还是很广的，如计算线性方程组的解的数目等，下面就看一下Math.NET中对该过程的计算实现以及如何调用的例子。

2.Math.NET矩阵秩计算的实现

　　Math.NET在对矩阵秩的计算过程中，和行列式的实现方式非常相似，也是把其作为矩阵计算的一个小部分功能，作为属性添加在各个矩阵分解算法的抽象和实现类中，看一下其中一个Svd分解算法抽象，由于计算简单，已经直接实现了秩的计算，继承类可以直接使用，就够了，其他的使用下面也和行列式类似。

internal abstract class Svd : Svd<float>
{
    protected Svd(Vector<float> s, Matrix<float> u, Matrix<float> vt, bool vectorsComputed)
        : base(s, u, vt, vectorsComputed) { }

    /// <summary>计算矩阵秩</summary>
    /// <value>The number of non-negligible singular values.</value>
    public override int Rank
    {
        get
        {
            return S.Count(t => !Math.Abs(t).AlmostEqual(0.0f));
        }
    }
    public override double L2Norm
    {
        get{return Math.Abs(S[0]);}
    }

    public override float ConditionNumber
    {
        get
        {
            var tmp = Math.Min(U.RowCount, VT.ColumnCount) - 1;
            return Math.Abs(S[0]) / Math.Abs(S[tmp]);
        }
    }
    /// <summary>计算行列式 </summary>
    public override float Determinant
    {
        get
        {
            if (U.RowCount != VT.ColumnCount)
            {
                throw new ArgumentException(Resources.ArgumentMatrixSquare);
            }

            var det = 1.0;
            foreach (var value in S)
            {
                det *= value;
                if (Math.Abs(value).AlmostEqual(0.0f))
                {
                    return 0;
                }
            }
            return Convert.ToSingle(Math.Abs(det));
        }
    }
}

3.Math.NET计算矩阵秩的代码

　　上述过程和原理只是便于大家理解其实现过程，下面简单演示一下在Math.NET中计算矩阵秩的过程，就是直接调用计算即可。

// 格式设置
var formatProvider = (CultureInfo)CultureInfo.InvariantCulture.Clone();
formatProvider.TextInfo.ListSeparator = " ";

//创建一个随机的矩阵
var matrix = new DenseMatrix(5);
var rnd = new Random(1); 
for (var i = 0; i < matrix.RowCount; i++)
{
    for (var j = 0; j < matrix.ColumnCount; j++)
    {
        matrix[i, j] = rnd.NextDouble();
    }
}

Console.WriteLine(@"Initial matrix");
Console.WriteLine(matrix.ToString("#0.00	", formatProvider));
Console.WriteLine();
//1. 秩
Console.WriteLine(@"矩阵秩计算结果为：");
Console.WriteLine(matrix.Rank());
Console.WriteLine();

结果如下：

Initial matrix
DenseMatrix 5x5-Double
0.25      0.11    0.47    0.77    0.66
0.43      0.35    0.94    0.10    0.64
0.03      0.25    0.32    0.99    0.68
0.65      0.28    0.62    0.70    0.70
0.95      0.09    0.16    0.38    0.80


矩阵秩计算结果为：
5

4.资源

　　包括源代码以及案例都可以去官网下载，下载地址本系列文章的目录中第一篇文章:http://www.cnblogs.com/asxinyu/p/4264638.html,有介绍。由于源码很大，如果找不到相应的案例，可以进行搜索，可以比较快的找到相应的代码。