1.


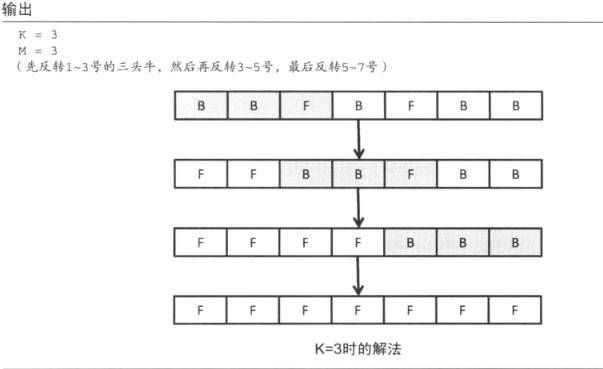
对于一个特定的 K 如何求出让所有牛面朝前方的最小操作数。如果把牛的方向作为状态进行搜索的话,由于状态数有 2N 个,是无法在时限内得出答案的。
首先,交换区间反转的顺序对结果是没有影响的。此外,对同一区间进行两次以上的反转是多余的。由此,问题就转化成了求需要被反转区间的集合。先考虑一下最左端的牛。包含这头牛的区间就只有一个,因此如果这头牛面朝前方,我们就能知道这个区间不需要反转。
反之,如果这头牛朝后方,对应的区间就必须反转。而且在此之后这个最左的区间就不需要考虑了。不断重复下去,就可以无需搜索求出最少需要的反转次数。
通过上面的分析可以知道,忽略掉对同一区间重复反转这类多余操作之后,只要存在让所有牛都朝前的方法,那么操作就和顺序无关可以唯一确定了。
这个算法的复杂度:首先需要对所有的 K 都求解一次,对于每个 K 都要从最左端开始来考虑 N 头牛的情况。此时最坏的情况下需要进行 N - K + 1 次的反转操作,而每次操作又要反转 K 头牛,于是总的复杂度为 O(N3)。这样还是不行,还需要对区间反转的部分进行优化。
f [ i ] := 区间 [ i, i + K - 1 ]进行了反转的话则为1,否则为0
这样,在考虑第 i 头牛时,如果![]() 为奇数的话,则这头牛的方向与起始反向是相反的,否则方向不变。由于
为奇数的话,则这头牛的方向与起始反向是相反的,否则方向不变。由于
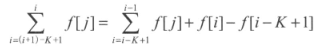
所以这个和每一次都可以用常数时间计算出来,复杂度降为 O(N2)
int N; int dir[MAX_N]; // 牛的方向(0:F, 1:B) int f[MAX_N]; // 区间[i, i + K - 1]是否进行反转 //固定K,求对应的最小操作数,无解的话则返回 -1 int calc(int K) { memset(f, 0, sizeof(f)); int res = 0; int sum = 0; for (int i = 0; i + K <= N; i++) { if ((dir[i] + sum) % 2 != 0) { res++; f[i] = 1; } sum += f[i]; if (i - K + 1 >= 0) sum -= f[i - K + 1]; } for (int i = N - K + 1; i < N; i++) { if ((dir[i] + sum) % 2 != 0) return -1; if (i - K + 1 >= 0) sum -= f[i - K + 1]; } return res; } void solve() { int K = 1, M = N; for (int k = 1; k <= N; k++) { int m = calc(k); if (m >= 0 && M > m) { M = m; K = k; } } printf("%d %d ", K, M); }
2.


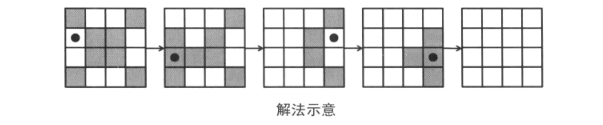
和 1 题一样,同一个格子(位置)翻转两次的话就会恢复原状,所以多次翻转是多余的。此外,翻转的格子的集合相同的话,其次序是无关紧要的。因此总共有 2NM 种方法,显然效率太低。
回顾一下 1 题,在 1 题中,让最左端的牛反转的方法只有一种,于是用直接判断的方法就可以确定。同样的方法是否在这里还行的通吗?
不妨先看一下最左上角的格子。在这里,除了翻转 (1, 1)之外,翻转(1, 2)和(2, 1)也可以把这个格子翻转,所以像之前那样直接确定的办法行不通。
于是不妨先指定好最上面一行的翻转方法。此时能够翻转(1, 1) 的只剩下(2, 1)了,所以可以直接判断(2, 1)是否需要翻转。类似地(2, 1)~(2, N)都能这样判断,如此反复下去就可以确定所有的格子的翻转方法。最后(M, 1)~(M, N)如果并非全为白色,就意味着不存在可行的操作方法。
像这样,先确定第一行的翻转方式,然后可以很容易判断这样是否存在解以及解的最小步数是多少,这样将第一行的所有的翻转方式都尝试一次之后就能求出整个问题的最小步数。这个算法中最上面一行的翻转方式共有 2N 种,复杂度为O(MN 2N)
// 邻接格子的坐标 const int dx[5] = {-1, 0, 0, 0, 1}; const int dy[5] = {0, -1, 0, 1, 0}; int M, N; int tile[MAX_M][MAX_N]; int opt[MAX_M][MAX_N]; //保存最优解 int flip[MAX_M][MAX_N]; // 保存中间结果 // 查询(x,y)的颜色 int get(int x, int y) { int c = tile[x][y]; for (int d = 0; d < 5; d++) { int x2 = x + dx[d]; int y2 = y + dy[d]; if (0 <= x2 && x2 < M && 0 <= y2 && y2 < N) c += flip[x2][y2]; } return c % 2; } //求出第 1 行确定情况下的最小操作次数,不存在解的话返回 -1 int calc() { //求出从第二行开始的翻转方法 for (int i = 1; i < M; i++) for (int j = 0; j < N; j++) if (get(i - 1, j) != 0) flip[i][j] = 1; // 判断最后一行是否是全白 for (int j = 0; j < N; j++) if (get(M - 1, j) != 0) return -1; //统计翻转的次数 int res = 0; for (int i = 0; i < M; i++) for (int j = 0; j < N; j++) res += flip[i][j]; return res; } void solve() { int res = -1; //按照字典序尝试第一行的所有可能性 for (int i = 0; i < 1 << N; i++) { memset(flip, 0, sizeof(flip)); for (int j = 0; j < N; j++) flip[0][N - j - 1] = i >> j & 1; // 这里不理解的话去看另一篇集合的整数表示 int num = calc(); if (num >= 0 && (res < 0 || res > num)) { res = num; memcpy(opt, flip, sizeof(flip)); } } if (res < 0) printf("IMPOSSIBLE "); else { for (int i = 0; i < M; i++) for (int j = 0; j < N; j++) printf("%d%c", opt[i][j], j + 1 == N ? ' ' : ' '); } }