1.本周学习总结(0--2分)
1.1.思维导图
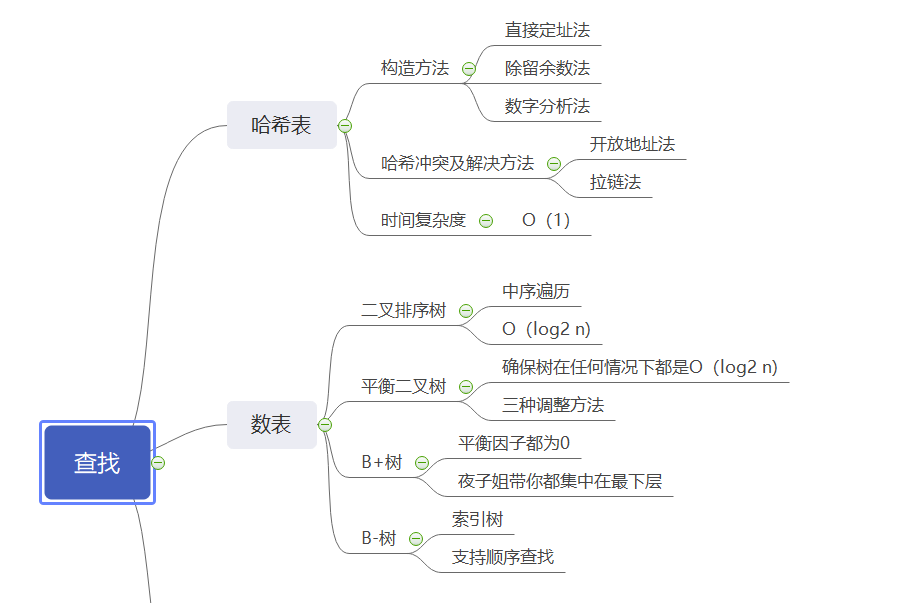
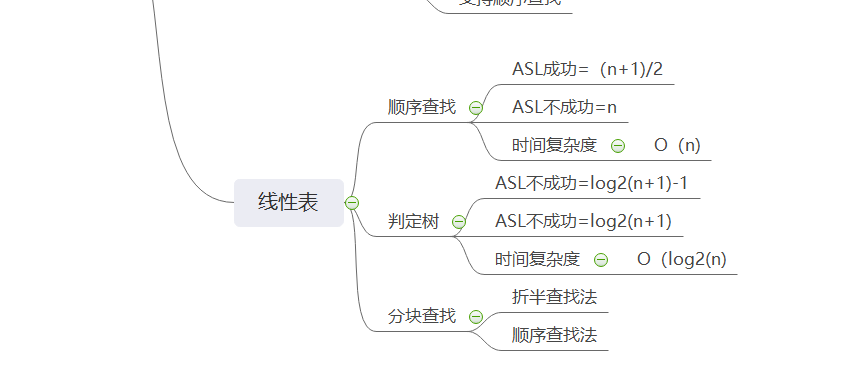
1.2谈谈你对查找运算的认识及学习体会。
这最后的这两周学习了查找,对一个元素的增删改,首先需要的就是需要查找,查找用关键字标识的一个数据元素,查找时根据给定的某个值,在表中确定一个关键字的值等于给定值的记录或数据元素。
在这章的学习里,有比较熟悉的线性表查找,数表查找运用了二叉树结构,二叉排序树的查找和树形有关,可以将其调整为平衡二叉树,根据失衡点,进行LL,RR,LR,RL三种调整,对于
树的节点增删改都是查找的重要要点
哈希表查找,之前有提过哈希数组,时间复杂度可以达到O(1),但是缺点就是要解决哈希冲突的问题,相对应的解决冲突的方法在上面的思维导图有提到
2.PTA实验作业(6分)
本周要求挑3道题目写设计思路、调试过程。设计思路用伪代码描述。题目选做要求:原则上题目选择越难,代码量越大分值越高。
2.1.题目1: 是否二叉搜索树 (25 分)
2.1.1设计思路(伪代码)
bool IsBST ( BinTree T )
{
if(非树或者非树的左右孩子)
return true;
定义树型 TLeft, TRight;
if(树的左孩子)
TLeft 往下走 该点左子树最大值;
if(树的右孩子)
TRight往下走 该点右子树最大值;
返回 (T->Left?(T->Data>TLeft->Data):1)&&(T->Right?(T->Data<TRight->Data):1);
}
2.1.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)
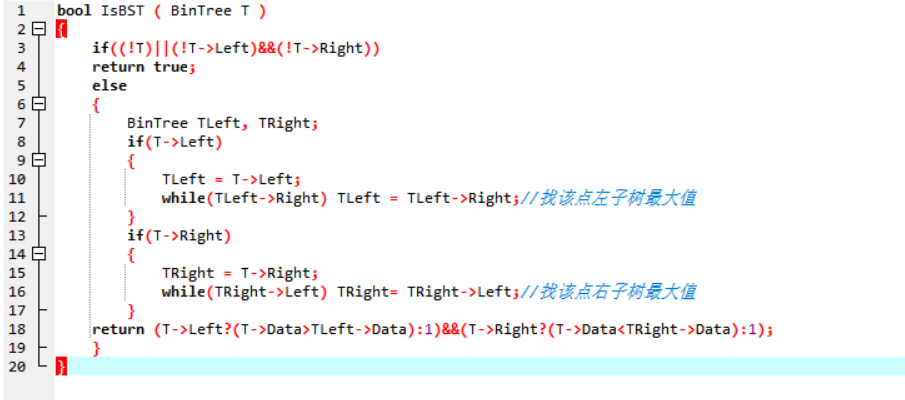
2.1.3本题PTA提交列表说明。

Q:一开始对左孩子的情况没有考虑进去
A:while(TLeft->Right) TLeft = TLeft->Right;
2.2.题目1二叉搜索树中的最近公共祖先 (25 分)
2.2.1设计思路(伪代码)
int Find( Tree T,int u)
{
if(树为空)
return 0;
if(关键字>u) return Find(T->Left,u);
if(关键字<u) return Find(T->Right,u);
if(关键字=u) return 1;
}
int LCA( Tree T, int u, int v )
{
if(树为空)
返回 ERROR;
if要查找的数存在
遍历到的结点大小在v和u之间,则该节点就是祖先
return T->Key;
遍历到的结点大小在v和u之间,则该节点就是祖先
return T->Key;
以下两个if表示两个结同在遍历到的结点的一侧
return LCA(T->Right,u,v);
否则: return LCA(T->Left,u,v)
end if
返回 ERROR;
}
2.2.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)
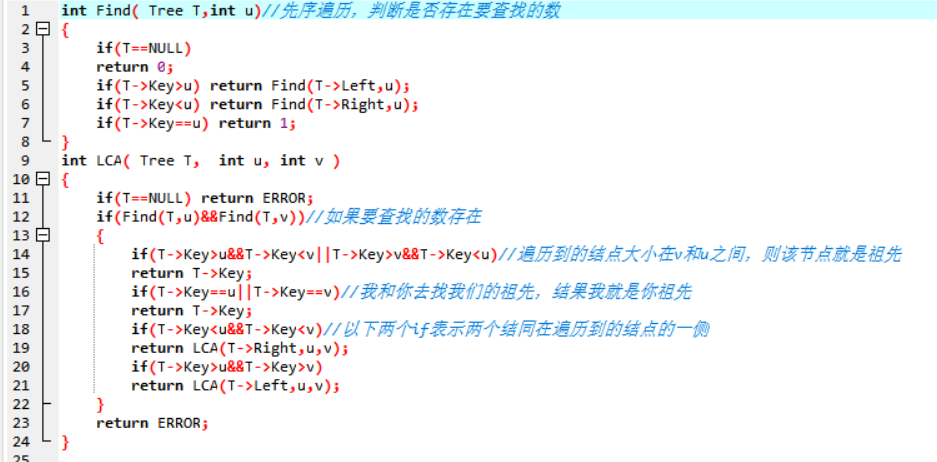
2.2.3本题PTA提交列表说明。

A:共同的祖先节点的关键在于向下的孩子们的关系
2.3.题目1:航空公司VIP客户查询 (25 分)
2.3.1设计思路(伪代码)
#include<bits/stdc++.h>(万能的编译预头,几乎包含所以的c/c++头文件)
map<string,int> m
定义 n,mi,k,e;
定义string类 s;
int main()
{
s.resize(20)(指定容器有效的元素个数20)
输入n mi
for(0 to n)
身份证号码输入进s数组中;
输入最低里程k, if(k<mi) k=mi;
m[s] += k;
end for
while(e to o)
身份证号码输入进s数组中;
定义we=m[s];
if(不为we)输出”No Info“;
else 输出 m[s];
2.3.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)
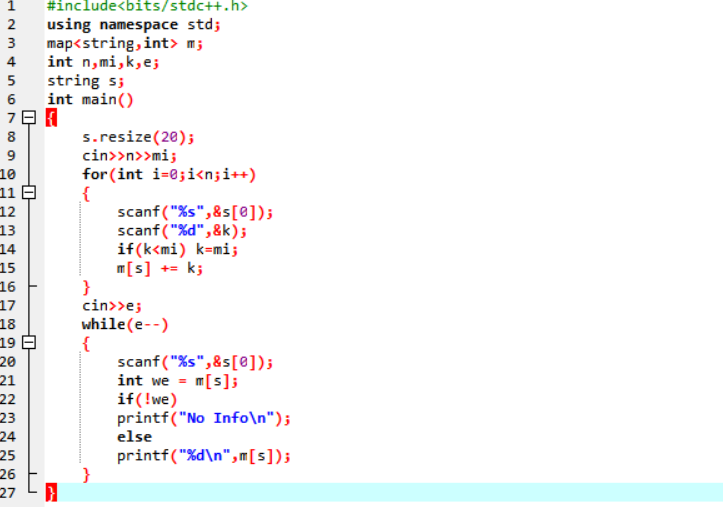
2.3.3本题PTA提交列表说明。

Q:这题难点在于对身份证这个常常的字符串的处理
A:使用图和string类可以大大简短代码量
3、阅读代码(-2--2分)
找一份和查找运算相关代码,谈谈你对这个代码认识体会。考研题种关于查找、二叉搜索树内容。
3.1 题目
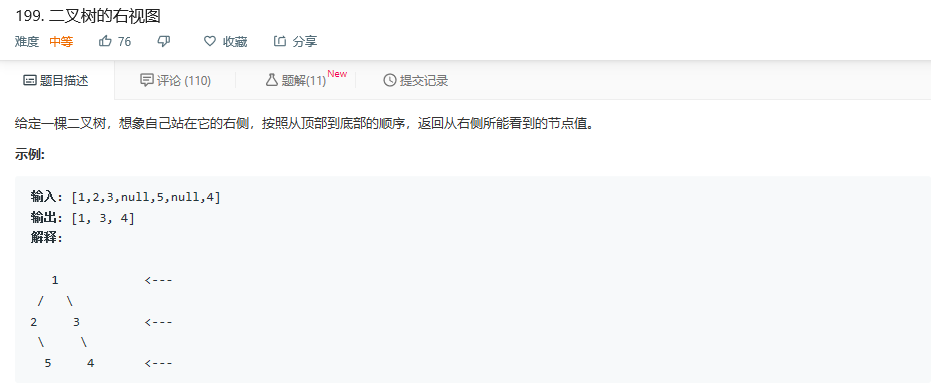
3.2 解题思路
解法一,递归法:
递归方法是分别遍历一个节点的右节点和左节点,因为是从右边看过来,所以我们需要首先遍历右节点。这里有个疑问,当遍历左节点时候,怎么判定它右边没有其他节点了呢?这里我们用到一个变量level,
对于同一层的节点,如果res数组的大小已经等于level了,说明右边已经有节点存入数组了,该节点就不用再保存。一直递归下去就可以得到结果
解法二,非递归法:
这道题要求我们打印出二叉树每一行最右边的一个数字,实际上是求二叉树层序遍历的一种变形,我们只需要保存每一层最右边的数字即可,还是需要用到数据结构队列queue,遍历每层的节点时,
把下一层的节点都存入到queue中,每当开始新一层节点的遍历之前,先把新一层最后一个节点值存到结果中
3.3 代码截图
递归方法:
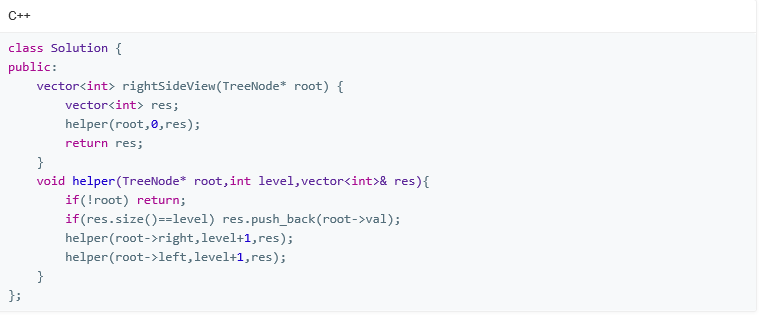
非递归方法:

3.4 学习体会
二叉树的右视图,相当于对二叉树进行层序遍历,将每一层的最后一个节点存入最终的结果即可,递归法与非递归法都有特点,不过递归法更加贴近二叉树的常规做法
- 题目以及解法来源于 力扣网。