1.本周学习总结
1.1思维导图
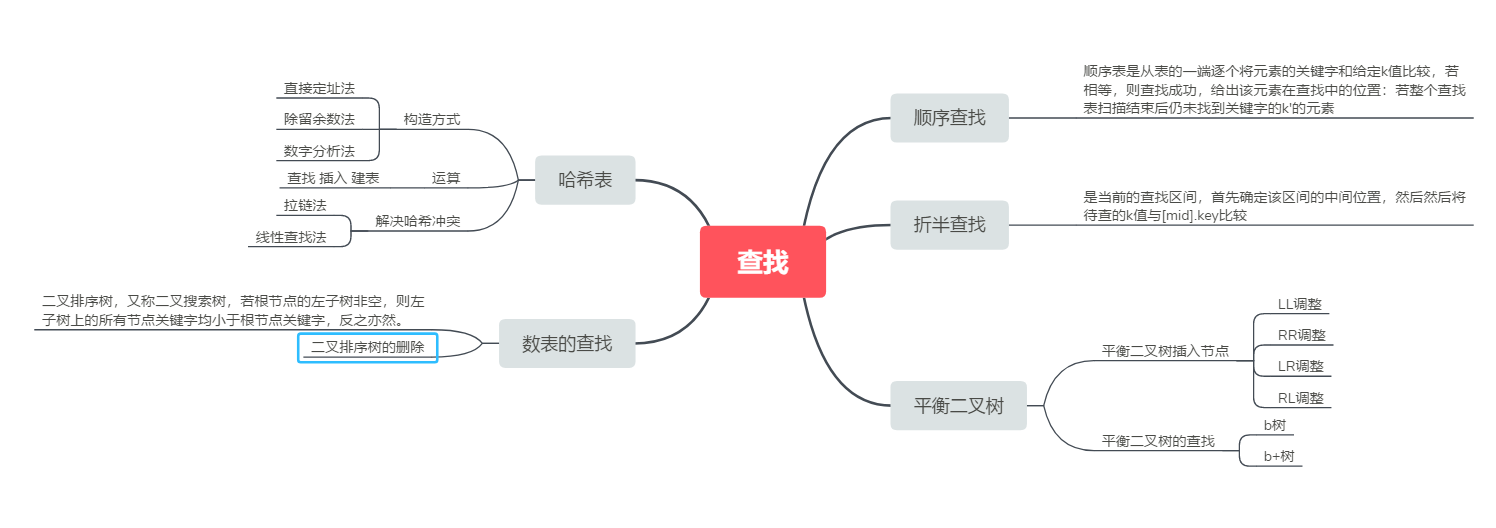
1.2谈谈你对查找运算的认识及学习体会
本周进行了查找的学习,查找的知识相对于图和树来说就更加的简单和容易理解。在查找这一章,主要的查找方法有哈希表还有很多高效率的排序方法,比如堆排序,归并排序,还有快速排序。在希尔表中,根据关键码值而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。其中产生的希尔冲突可以用线性探查法和希尔链法来进行解决。在排序中,我们所学的高效的排序算法的时间复杂都是n(nlog2n),但是快速排序依旧是其中最佳,虽然他们都是高效的算法,但是这些算法都不稳定。
2.PTA实验作业
2.1.题目1:6-2 是否二叉搜索树
2.1.1设计思路
定义全局变量 数组a i=0;
判断函数
if 根节点不为0
执行左节点的递归;
将该节点的数据保存到a数组中;
执行右节点的递归;
end if
for j=0 to i
if a数组中的j个元素比j-1小
则为非搜索二叉树
反之则为搜索二叉树
2.1.2代码截图

2.1.3本题PTA提交列表说明

说明
- 一开始未将数组a和i定义成全局变量,导致在递归的时候将a和i都重新定义一遍。
- 将j的循环从0开始,导致在空树的时候会输出不存在的节点。
2.2.题目2:6-3 二叉搜索树中的最近公共祖先
2.2.1设计思路
Find函数
if 节点为空 return 0;end if
if 节点的数值等于u return 1; end if
if 节点的数值小于u 执行右孩子的递归; end if
if 节点的数值大于u 执行左孩子的递归; end if
LCA函数
if 节点为空 return ERROR; end if
if(Find(u)=1且Find(v)=1)
if (u小于t且v大于t)或者(v小于t且u大于t)
返回t的值; end if
if (u和v其中一个等于t)
返回t的值; end if
if(u<t) 执行左孩子的递归 end if
if(v>t) 执行右孩子的递归 end if
如果Find(u)=1且Find(v)不为一1
return ERROR;
2.2.2代码截图
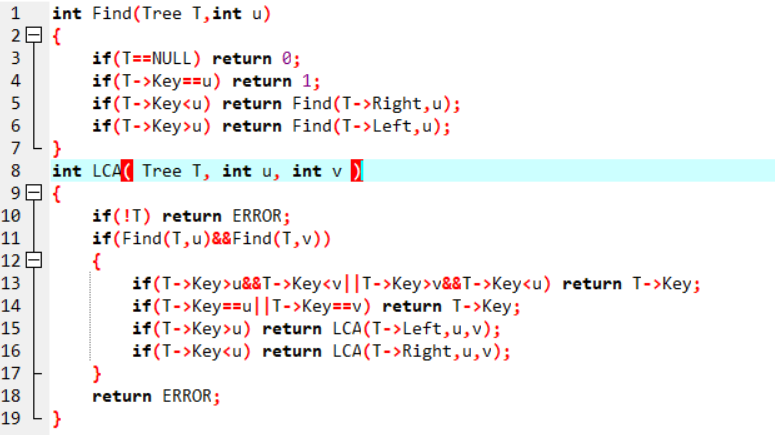
2.2.3本题PTA提交列表说明
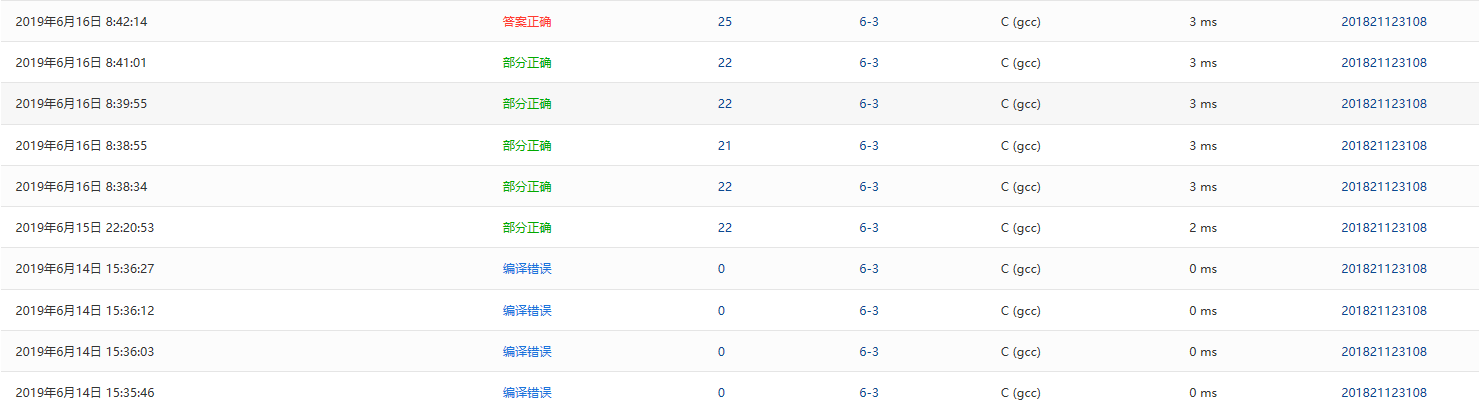
说明:
- 编译错误是之前key的k忘记大写了,好难看出来
 。
。 - 将LCA中递归的部分,多加了个v的判断,这样会导致一些递归的步骤被跳过。
- 一开始忘记考虑u和v都在一边子树上的情况。
2.3.题目3 7-1 QQ帐户的申请与登陆
2.3.1设计思路
定义两个map容器 p和pp
输入 n
while(n递减)
输入字符 x,y,z
if(x为登入)
if p对应账号的键值为0 则该账号不存在 end if
else 如果pp对应账号的密码不符 则输出密码错误
else 登入成功
end if
if(x未注册)
如果该账号对应p数组的值为一 则账号已经存在
if 账号还没被祖册
将对应账号的p数组的值改为1
将对应账号的pp数组的值改为密码
输出注册成功
2.3.2代码截图

2.3.3本题PTA提交列表说明

说明:
- 这是我第一次尝试用map容器来写代码,感觉还不错,就是用一个键值代替了一个可能复杂的字符串。
- 忘记将存在时的p数组的y值改为1。
3.阅读代码(acm考题)
## 3.1 题目
在一个给定形状的棋盘(形状可能是不规则的)上面摆放棋子,棋子没有区别。要求摆放时任意的两个棋子不能放在棋盘中的同一行或者同一列,请编程求解对于给定形状和大小的棋盘,摆放k个棋子的所有可行的摆放方案C。
Input
输入含有多组测试数据。
每组数据的第一行是两个正整数,n k,用一个空格隔开,表示了将在一个n*n的矩阵内描述棋盘,以及摆放棋子的数目。 n <= 8 , k <= n
当为-1 -1时表示输入结束。
随后的n行描述了棋盘的形状:每行有n个字符,其中 # 表示棋盘区域, . 表示空白区域(数据保证不出现多余的空白行或者空白列)。
Output
对于每一组数据,给出一行输出,输出摆放的方案数目C (数据保证C<2^31)。
Sample Input
2 1
#.
.#
4 4
...#
..#.
.#..
#...
-1 -1
Sample Output
2
1
3.2 解题思路
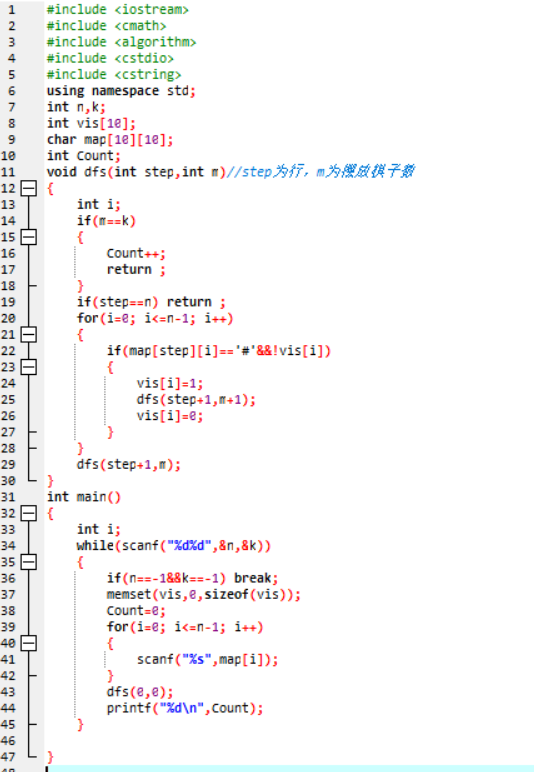
该题是n皇后问题的变种,不过没有abs(i-j)=abs(a[i]-a[j])的条件,即没有对角线的条件,vis[i]表示搜索过了列,step表示行用一下dfs就好了,下面的dfs(step+1,m)是在step行没有放棋子的条件,记得回溯就可以做出题目了。对于这道题大多数用的是进行层层深搜的思想,用一个数组来记录每列的状态,需要中间判断下放不放子的问题就行了,数据量因为n<=8,所以不存在什么问题。
3.3 代码截图
3.4 学习体会
dfs真的是一个很好用的遍历方式,微信朋友圈用的就是这种遍历,我们只能看到共同好友的评论。在许多题目中用dfs遍历,往往会省下很多的步骤。