一、理论
聚类就是把东西聚在一起,那一定有一定的规则,相似等,后面会给出。聚类与分类的不同就是,聚类所要求的划分的类是未知的。聚类是这么定义的:将数据分类到不同的类或者簇这样的一个过程,所以同一个簇中的对象有很大的相似性,而不同簇之间的对象很大的相异性。按照个体或样品(individuals, objects or subjects)的特征将它们分类,使同一类别内的个体具有尽可能高的同质性(homogeneity),而类别之间则应具有尽可能高的异质性(heterogeneity)。

传统的聚类有:系统聚类法,分解法,加入法,动态聚类法,有序样品聚类,有重叠聚类和模糊聚类。其中,我们很熟悉的就是K-均值、K-中心点等算法,经典以后可以单独来说这个
两种相似性度量:距离和相似系数
- 采用描述个体对(变量对)之间的接近程度的指标,例如“距离”,“距离”越小的个体(变量)越具有相似性。
- 采用表示相似程度的指标,例如“相关系数”,“相关系数”越大的个体(变量)越具有相似性。
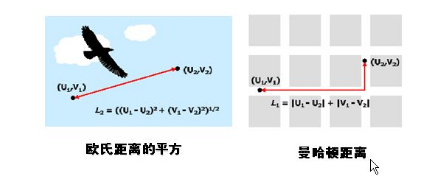
再多说一点距离:用来度量样品之间的相似性,聚类——距离指标D(distance)的方法非常多:按照数据的不同性质,可选用不同的距离指标。欧氏距离(Euclidean distance)、欧氏距离的平方(SquaredEuclidean distance)、曼哈顿距离(Block)、切比雪夫距离(Chebychev distance)、卡方距离(Chi-aquaremeasure) 等;相似性也有不少,主要是皮尔逊相关系数。
方法一:系统聚类法的基本思想:令n个样品自成一类,计算出相似性测度,此时类间距离与样品间距离是等价的,把测度最小的两个类合并;然后按照某种聚类方法计算类间的距离,再按最小距离准则并类;这样每次减少一类,持续下去直到所有样品都归为一类为止。聚类过程可做成聚类谱系图(Hierarchical diagram)。这里的距离有很多例如最短距离法
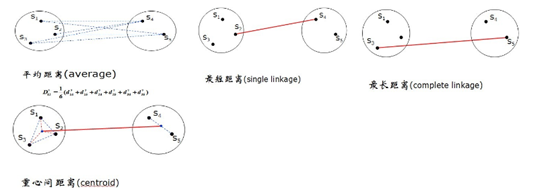
l最短距离法(singlelinkage) l最长距离法(completelinkage) l中间距离法(medianmethod) l可变距离法(flexiblemedian) l重心法(centroid) l类平均法(average) l可变类平均法(flexibleaverage) lWard最小方差法(Ward’sminimum variance)
注意:最长距离法,可变类平均法,离差平方和,注意这些都是有单调性的,中间距离法和重心性不具有单调性。这里的相似性:用来度量变量之间对相似性,r的绝对值接近1,就表示相关或者相似。
步骤:
s1.构造n个类,每个类包含且只包含一个样品。 s2.计算n个样品两两间的距离,构成距离矩阵,记作D0。 s3.合并距离最近的两类为一新类。 s4.计算新类与当前各类的距离。若类的个数等于1,转到步骤(5),否则回到步骤(3)。 s5.画聚类图。 s6.决定类的个数,及各类包含的样品数,并对类作出解释。
二、实现
Matlab提供系列函数用于聚类分析,归纳起来具体方法有如下三种
方法一:直接聚类,利用clusterdata函数对样本数据进行一次聚类,其缺点为可供用户选择的面较窄,不能更改距离的计算方法,该方法的使用者无需了解聚类的原理和过程,但是聚类效果受限制。
方法二:层次聚类,该方法较为灵活,需要进行细节了解聚类原理,具体需要进行如下过程处理
(1)找到数据集合中变量两两之间的相似性和非相似性,用pdist函数计算变量之间的距离;
(2)用 linkage函数定义变量之间的连接;
(3)用 cophenetic函数评价聚类信息;
(4)用cluster函数创建聚类。
方法三:划分聚类,包括K均值聚类和K中心聚类,同样需要系列步骤完成该过程,要求使用者对聚类原理和过程有较清晰的认识。
Matlab中的相关函数和相关聚类方法
pdist函数
用格式:Y=pdist(X,’metric’) 说明:用 ‘metric’指定的方法计算 X 数据矩阵中对象之间的距离。 X:一个m×n的矩阵,它是由m个对象组成的数据集,每个对象的大小为n(即n个特征值)。 metric’取值如下: ‘euclidean’:欧氏距离(默认);
‘seuclidean’:标准化欧氏距离; ‘mahalanobis’:马氏距离;
‘cityblock’:布洛克距离; ‘minkowski’:明可夫斯基距离; ‘cosine’: ‘correlation’: ‘jaccard’:‘chebychev’:Chebychev距离。
squareform 函数
Z = squareform(Y,..)
对于M个点的数据集X,pdist之后的Y将是具有M*(M-1)/2个元素的行向量。Y这样的显示虽然节省了内存空间,但对用户来说不是很易懂,如果需要对这些距离进行特定操作的话,也不太好索引。MATLAB中可以用squareform把Y转换成方阵形式,方阵中<i,j>位置的数值就是X中第i和第j点之间的距离,显然这个方阵应该是个对角元素为0的对称阵。
linkage函数
Z=linkage(Y,‘method’) 输入值说明:Y为pdist函数返回的M*(M-1)/2个元素的行向量,用‘method’参数指定的算法计算系统聚类树。 method:可取值如下: ‘single’:最短距离法(默认); ‘complete’:最长距离法; ‘average’:未加权平均距离法; ‘weighted’: 加权平均法; ‘centroid’:质心距离法; ‘median’:加权质心距离法; ‘ward’:内平方距离法(最小方差算法) 返回值说明:Z为一个包含聚类树信息的(m-1)×3的矩阵,其中前两列为索引标识,表示哪两个序号的样本可以聚为同一类,第三列为这两个样本之间的距离。另外,除了M个样本以外,对于每次新产生的类,依次用M+1、M+2、…来标识。
dendrogram函数
调用格式:[H,T,…]=dendrogram(Z,p,…) 说明:生成只有顶部p个节点的冰柱图(谱系图)。 为了表示Z矩阵,我们可以用更直观的聚类数来展示,方法为:dendrogram(Z), 产生的聚类数是一个n型树,最下边表示样本,然后一级一级往上聚类,最终成为最顶端的一类。纵轴高度代表距离列。 另外,还可以设置聚类数最下端的样本数,默认为30,可以根据修改dendrogram(Z,n)参数n来实现,1<n<M。dendrogram(Z,0)则表n=M的情况,显示所有叶节点。
cophenet函数
c=cophenet(Z,Y) 说明:利用pdist函数生成的Y和linkage函数生成的Z计算cophenet相关系数。 cophene检验一定算法下产生的二叉聚类树和实际情况的相符程度,就是检测二叉聚类树中各元素间的距离和pdist计算产生的实际的距离之间有多大的相关性,另外也可以用inconsistent表示量化某个层次的聚类上的节点间的差异性。
cluster 函数
调用格式:T=cluster(Z,…) 说明:根据linkage函数的输出Z 创建分类。
clusterdata 函数
调用格式:T=clusterdata(X,…) 说明:根据数据创建分类。 When 0 < CUTOFF < 2, T = CLUSTERDATA(X,CUTOFF) is equivalent to: Y = pdist(X, 'euclid'); Z = linkage(Y, 'single'); T = cluster(Z, 'cutoff', CUTOFF); When CUTOFF is an integer >= 2, T = CLUSTERDATA(X,CUTOFF) isequivalent to: Y = pdist(X,'euclid'); Z = linkage(Y,'single'); T = cluster(Z,'maxclust',CUTOFF)
Inconsistent函数
S_i是除了叶节点外,所有深度低于(M+i)不超过DEPTH的节点(包括M+i节点自身) 而Inconsistent计算的是S_i的距离的平均值,Then Y(i,1) = mean(Z(S_i,3)), the mean height of nodes in S_i Y(i,2) = std(Z(S_i,3)), the standard deviation of node heights in S_i Y(i,3) = length(S_i), the number of nodes in S_i Y(i,4) = (Z(i,3) - Y(i,1))/Y(i,2), the inconsistent value The default value for DEPTH is 2.
计算深度会影响不一致系数的计算结果,计算深度比较大时,不一致系数的增量能反映出当前步引入的新样品与该类中心(涉及该类中所有样品)的距离远近,计算深度比较小时,不一致系数的增量仅能反映出当前步引入的新样品与上几步聚类中涉及的样品的中心的距离远近。
方法一:一次聚类法(直接使用clusterdata函数)
x1=randn(10,1);
x2=randn(10,1)+10;
x3=randn(10,1)+20;
x=[x1;x2;x3];
y=randn(30,1);
T=clusterdata([x,y],3)
temp1=find(T==1)
plot(x(temp1),y(temp1),'rd','markersize',10,'markerfacecolor','r')
hold on
temp1=find(T==2)
plot(x(temp1),y(temp1),'yd','markersize',10,'markerfacecolor','y')
temp1=find(T==3)
plot(x(temp1),y(temp1),'kd','markersize',10,'markerfacecolor','k')
legend('cluster 1','cluster 2','cluster 3')
结果如下图:

方法二和方法三设计流程:分步聚类
Step1 寻找变量之间的相似性,用pdist函数计算相似矩阵,有多种方法可以计算距离,进行计算之前最好先将数据用zscore函数进行标准化。
X2=zscore(X); %标准化数据 Y2=pdist(X2); %计算距离 Step2 定义变量之间的连接 Z2=linkage(Y2); Step3 评价聚类信息 C2=cophenet(Z2,Y2); //0.94698 Step4 创建聚类,并作出谱系图 T=cluster(Z2,6); H=dendrogram(Z2);