动态规划
public class Solution { public int NumSquares(int n) { var list = new List<int>(); list.Add(0); for (int i = 1; i <= n; i++) { list.Add(i);//每一个数字,初始化为全部由1构成 } for (int i = 2; i <= n; i++) { for (int j = 1; j * j <= i; j++) { var x = list[i];//当前值的构成数量,由全部是1来构成 var s = i - j * j;//减去一个平方数后的余数 var t = list[s];//余数值的构成数量 var y = t + 1;//因为减过j*j,因此用余数的构成数量+1,相当于计算原值的构成数量 list[i] = Math.Min(x, y); } } return list[n]; } }
补充一个python的实现,在leetcode上会TLE,经查询发现在讨论区中也有其他的人遇到了相同的TLE问题。
应该是对python语言的判断机制有问题,这种“平台语言杀”的问题出现过多次了。
1 class Solution: 2 def numSquares(self, n: int) -> int: 3 dp = [0] * (n + 1) 4 #初始化,所有的数字都由'1'组成,dp中每个元素值为组成的数量 5 for i in range(1,n+1): 6 dp[i] = i 7 for i in range(2,n+1): 8 for j in range(1,int(i**0.5)+1): 9 res = i - j * j#减去一个完全平方数后的剩余值 10 dp[i] = min(dp[i],dp[res] + 1) 11 return dp[n]
经过修改可以AC了,但是效率是比较低的:
1 class Solution: 2 def numSquares(self, n: int) -> int: 3 dp = list(range(n+1)) 4 for i in range(2,n+1): 5 for j in range(1,int(i**0.5)+1): 6 res = i - j * j#减去一个完全平方数后的剩余值 7 dp[i] = min(dp[i],dp[res] + 1) 8 return dp[n]
既然python不能用dp方法提交,那就再提供一种别的思路,使用广度优先遍历(BFS):
1 class Solution: 2 def numSquares(self, n: int) -> int: 3 power = set() 4 base = 1 5 #生成符合条件的所有完全平方数,存储在power集合中 6 while base*base <= n: 7 curnum = base*base 8 if curnum == n: 9 return 1 10 power.add(curnum) 11 base += 1 12 #level为返回值,表示最少的完全平方数的数量 13 level = 1 14 #初始目标设置为n 15 target = {n} 16 #判断条件target不为空 17 while len(target) > 0: 18 cur = set() 19 #在目标集合中循环,获得一个值 20 for i in target: 21 #在完全平方数集合中循环,获得一个值 22 for e in power: 23 #目标值 - 某个完全平方数 的差值,也是完全平方数 24 if i-e in power: 25 #返回 当前level + 1 26 return level+1 27 #目标值 - 某个完全平方数 的差值,不是完全平方数,且大于0 28 if i-e > 0: 29 #将这个差值存储在‘下一层’ 30 cur.add(i-e) 31 #用下一层的值更新target 32 target = cur 33 #层级+1 34 level += 1
以n=15为例,其计算流程如下:
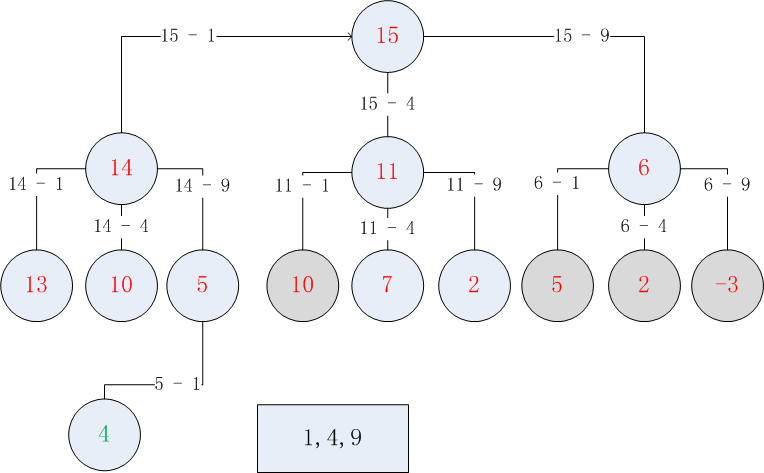
先计算小于等于15的值中,所有的完全平方数,如上图矩形区域所示(1,4,9)三个数值。
第一层的target中的值是:(15),用15分别减去power中的数值,得到第二层;
第二层的target中的值是:(14,11,6),三个数字都不在target集合中,因此继续计算第三层,用这三个数字分别减去power中的数值,得到第三层;
第三层的target中的值是:(13, 10, 5, 10, 7, 2, 5, 2, -3),其中10,5,2出现了重复,使用set会自动去重,而-3 小于0,也会被过滤掉,
最终得到第三层的数值为:(13,10,5,7,2),这五个数字都不在power中,因此继续用这5个数字计算第四层:
当计算5时,可得到 5 - 1 = 4,而4在power中,因此结束循环。此时节点5所在的“树的高度”为3(根结点从1开始计算),因此level + 1 等于4。
最终返回4,即为所求,最终的完全平方数的组合是由线上的被减的值和叶子节点的值组成,即:[1,9,1,4]。