kmp代码:
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#define N 100
char text[N], pattern[N];
void move(int prefix[], int n) // 对 prefix 表 进一步处理
{
for (int i = n - 1; i > 0; i--) // 整体后移
prefix[i] = prefix[i - 1];
prefix[0] = -1;
/*for (int i = 0; i < n; i++)
{
printf("%d ", prefix[i]);
}puts("");*/
}
void prefix_table(int prefix[], int n) // 打印 prefix 表
{
prefix[0] = 0; // 只有一位没有前后缀
int len = 0;
int i = 1;
while (i < n) // 用 while 不用 for, 可以同时实现 求所有子串的最缀 及当前子串的多次查找最缀
{
if (pattern[i] == pattern[len])
{
len++;
prefix[i++] = len;
}
else if (len > 0)
len = prefix[len - 1]; // 当前子串的 最缀 还没找到,再次循环
else
prefix[i++] = len; //此时 len==0
}
move(prefix, n);
}
void kmp_search()
{
int n = strlen(pattern);
int m = strlen(text);
int *prefix = (int*)malloc(sizeof(int)*n);
prefix_table(prefix, n);
// pattern 用 j , text 用 i
int i = 0, j = 0, ci = 0;
while (i < m&&j < n)
{
if (j == n - 1 && text[i] == pattern[j]) // j==n-1 对应 j 移动到 pattern 的最后一位,如果这一位仍然相等的成功匹配了
{
printf("找到了第 %d 个 ,起始位置在 %d 位置
", ++ci, i - j);
j = prefix[j];
i++;
continue;
}
if (text[i] == pattern[j])
i++, j++;
else
j = prefix[j]; //这句是精髓啊
if (j == -1) // -1是为了 这种情况可以特殊处理
j++, i++;
}
}
int main(void)
{
printf("请输入要找的主串text: ");
scanf("%s", text);
printf("请输入要找的模式串pattern: ");
scanf("%s", pattern);
kmp_search();
system("pause");;
return 0;
}
一,关于最长公共前后缀的理解
1,首先最。。不能包含自身
所以 prefix[0]=0
2, 虽然字符串 aba 是对称的,但是其最长公共前后缀为 a
因为 若其最长公共前后缀长度为2的话,则前缀为 ab,后缀为 ba ,两者不同
3,prefix 要增加就只能是一次加 1 的递增,
因为 前缀始终是不变的,变的是后缀,且后缀也只是每次 加上一个字符,
所以最长公共前后缀最多也只能一次加 1
4,len
len 指向 ((当前字符串去掉最后一位的字符串) 的最长公共前后缀) 的最后一个位置 在加一位
为什么指向这里呢? 看一下例子就能 明白了。
对于 ABAAB ,
当前字符串去掉最后一位的字符串 为 ABAA
(当前字符串去掉最后一位的字符串) 的最长公共前后缀 为 A
((当前字符串去掉最后一位的字符串) 的最长公共前后缀) 的最后一个位置 在加一位 为 第一个B 的位置
对于 ABAAB 这个字符串 ,已知 ABAA 的最长公共前后缀为 A,长度为 1,
ABAAB 要想在 ABAA 的基础上,让最长公共前后缀增加,只能是 比较 第五个字符 与 第一个B
5,接下来就是我自己的 彼得一激灵,即对 len=prefix[len-1] 和 j=prefix[j] 的理解:
这两句的原理是一样的,都是根据前面子串的最长公共前后缀 去 减少匹配数次,
至于 j 为什么不用减 1,因为 prefix_table 整个往后移了一位。
设 A 为最长公共前后缀 ,B为不相干字符串,a为最长公共前后缀的最长公共前后缀, b,c 为不相干字符串
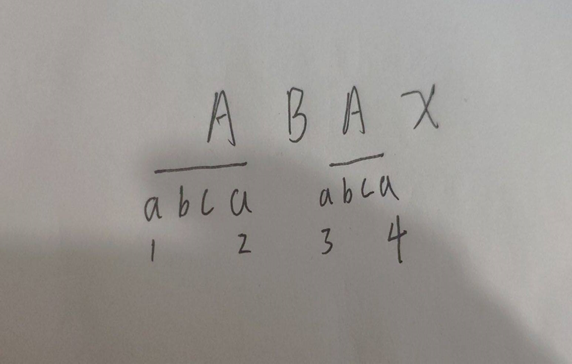
已知 ABA 的最长公共前后缀已经算好了,为 A ,接下来要算 ABAx 的:
首先 比较 B 与 x ,若相等,则长度可知。
若不相等,由于原长度是在 a2 位置,但应退回 a1 置,即最长公共前后缀的最长公共前后缀, 而不是 c 。
因为此时 ABA 的第二长公共前后缀是 a1 和 a4 ,即使 x==c,也无用。
另外,附上我自己走一遍的流程图:

三,这是 kmp_search 函数的流程图
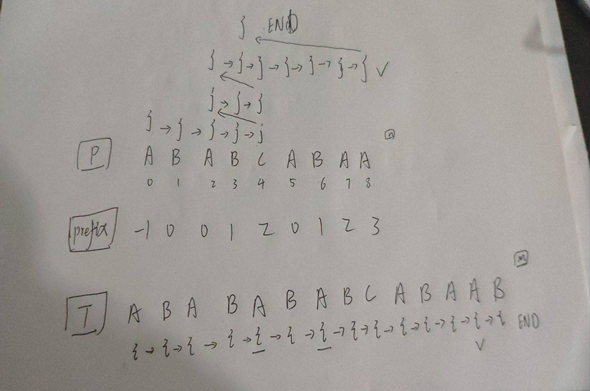
三,move 函数(比较 两次函数两次匹配)
因为每次无法匹配时,都要找前一个子串的最长公共前后缀,且为了考虑前一个子串的所有前后缀也都匹配不上的情,
且 pattern 的最长公共 前后缀 我们无需关心,因为这一位 匹配成功 的就结束了,匹配不成功的话 关心的是前一个子串的最长公共前后缀,
所以,为了写代码的方便,我们直接让前缀表后移一位,第一位的 -1,当成 是 前一个子串的所有前后缀也都匹配不上的情况。
END
============ ======== ======== ======= ====== ===== ==== === == =
路还是要自己走过才知道。
The road or to know through their own.