网络流初步

图片内容并非原创，来自巨神学长
2020/1/14更新：修复了最大流板子常数过大的问题

最大流

设G(V,E)为一个有向图，它的每条边<u,v>都被赋予了一个非负的实数c作为边的容量，记为c(u,v)。网络流
(network flow)指为这个有向图分配流并且使得它每条边上的流量都不能超过这条边的容量。
在运筹学中，有向图称为网络，边称为弧(arc)。在这个有向图中指定两个顶点分别叫做源点Vs和汇点Vt。
除源点和汇点，要保持每个顶点进出总流量相同，源点的总出流量和汇点的总入流量相等。

Dinic算法

Dinic算法基本步骤

1. 初始化网络及其网络流

2. 构造剩余网络和层次网络，若汇点不在层次网络中则算法结束。

3. 在层次图G_L内用一次DFS过程进行增广每次都向层次增加1的方向增广，每次增广完毕，在层次网络中要去掉
   因改进流量而导致饱和的弧，DFS执行完毕则该阶段增广完毕。

4. 转步骤2。

复杂度

实际复杂度(O(V^2E))

小贴士：在实际运行中远远达不到这个上界，一般可以护理 到 规模的算法.其中求解二分图时有更好的复杂度(O(msqrt n ))且实际上的复杂度比这个更加优秀

Dinic算法演示

首先设maxflow=0
如图，源点为0，汇点为5，首先对其建立层次图

每个顶点右下方的数字就是其对应的层次。接下来进行DFS，找到一条流量为4的增广路。

此时maxflow=4

回退至顶点3，发现它没有其他的允许弧，继续回退至1。在回退的过程中不断修改流经的弧的容量。接下来，发现顶点1有一个允许弧连至4，继续DFS。此时流量上限已经更新为10-4=6（指<0,1>边）。

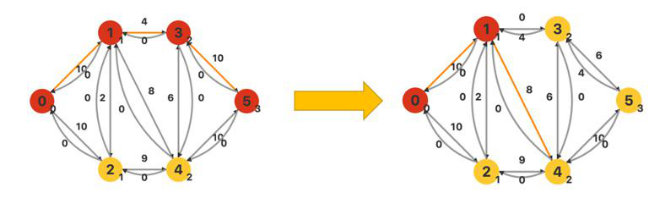
又找到一条流量为min(6,8,10)=6的增广路。

此时的最大流量maxflow=4+6=10

此时顶点1的流量上限已经为0，从顶点1回退至源点。修改相关弧的剩余容量。

继续搜索源点的相邻顶点2，并找到一条增广路。由于源点的容量上限始终是INF，所以增广路的流量为min(10,9,4)=4。

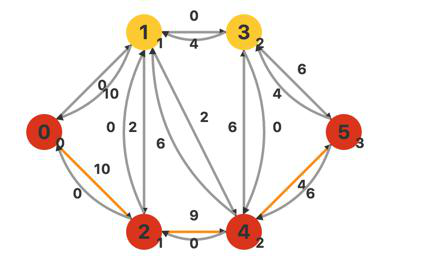
此时的最大流量为maxflow=4+6+4

此时节点二已经跑满，回退到源点，并调整相应的弧的容量，发现源点没有其他的相邻顶点，dfs过程结束

再次BFS，重新建立层次图

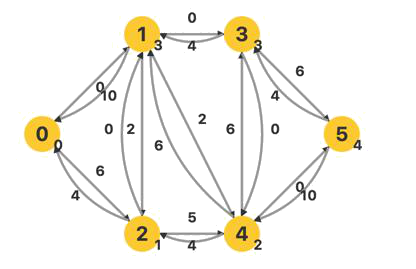
找到一条增广路，流量为min(6,5,6,6)=5

此时的最大流量maxflow=4+6+4+5

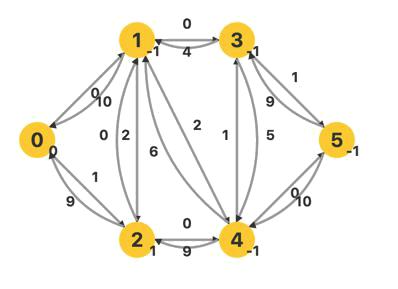
发现没有其他增广路，回退至源点，更新相关弧的容量。

源点没有其他的相邻点，重新BFS建立新的层次网络，发现汇点不在层次网络中，算法结束

例题 HDU-1532 Drainage Ditches

题目链接：

https://vjudge.net/problem/HDU-1532

题解

最大流裸题，题意是有n个沟渠，能够流过一定量的水，有m个池塘，1为源点，m为汇点，求最大流

使用vector建图在网络流里十分不方便，找到反向边比较麻烦，在之后的最小费用最大流中更是十分麻烦，所以采用链式前向星建图

AC代码

#include <cstdio>
#include <vector>
#include <algorithm>
#include <iostream>
#include <queue>
#include <cstring>
#define N 250
using namespace std;
const int inf = 0x3f3f3f3f;
int m, n;
struct node {
	int u, v, cap, nxt;
	node () {}
	node (int u, int v, int cap, int nxt): u(v), v(v), cap(cap), nxt(nxt) {}
} edge[N * 10];
int head[N], tot;
void init() {
	memset(head, -1, sizeof(head));
	tot = 0;
}
int dep[N];
void adde(int u, int v, int w) {
	edge[tot] = node(u, v, w, head[u]);
	head[u] = tot++;
	edge[tot] = node(v, u, 0, head[v]);
	head[v] = tot++;
}
bool bfs(int s, int t) {
    queue<int> q;
    memset(dep, -1, sizeof(dep));
    dep[s] = 0;
    q.push(s);
    while (!q.empty()) {
        int u = q.front(); q.pop();
        for (int i = head[u]; ~i; i = edge[i].nxt) {
            int v = edge[i].v;
            if (edge[i].cap > 0 && dep[v] == -1) {
                dep[v] = dep[u] + 1;
                q.push(v);
            }
        }
    }
    return dep[t] > 0;
}
int dfs(int u, int t, int f) {
    if (u == t) return f;
    int w, used = 0;
    for (int i = head[u]; ~i; i = edge[i].nxt) {
        int v = edge[i].v;
        int cap = edge[i].cap;
        if (cap && dep[v] == dep[u] + 1) {
            w = f - used;
            w = dfs(v, t, min(w, cap));
            edge[i].cap -= w;
            edge[i ^ 1].cap += w;
            used += w;
            if (used == f) return f;
        }
    }
    if (!used) dep[u] = -1;
    return used;
}
int dinic(int s, int t) {
    int maxflow = 0;
    while (bfs(s, t)) {
       maxflow += dfs(s, t, inf);
    }
    return maxflow;
}
int main() {
	while (~scanf("%d%d", &m, &n)) {
		init();
		for (int i = 1; i <= m; i++) {
			int u, v, w;
			scanf("%d%d%d", &u, &v, &w);
			adde(u, v, w);
		}
		printf("%d
", dinic(1, n));
	}
	return 0;
}

最小割

最大流即最小割

最小费用最大流

在一个网络中，可能存在多个总流量相同的最大流f，我们可以在计算流量的基础之上，给网络中的弧增加一个单位流量的费用（简称费用），在确保流量最大的前提下总费用最小，这样的最大流被称为最小费用最大流。

在下面这个网络中，弧上有逗号分隔的两个数分别为弧的容量和单位流量费用。例如，一条流量为2、经过S->1->4->T的流的费用为(3+5+4)*2=24。

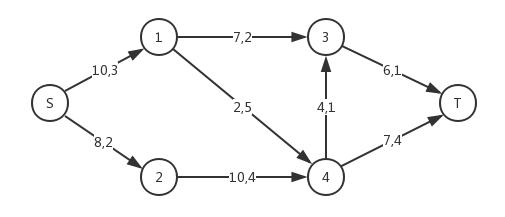
基本步骤

1. 网络初始流量为 0

2. 在当前的剩余网络上求出从 S 到 T 的最短增广路 min_dist(s,t) ，以每条弧的单位流量费用为边权，“距离”即为该路径上的边的单位费用之和。如果不存在，则算法结束

3. 找出这条路径上的边的容量的最小值 f ，则当前最大流 max_flow 扩充 f ，同时当前最小费用 min_cost 扩充 f * min_dist(s,t) 。

4. 修改增广路上弧的流量（正向边的容量减少 f ，反向边的容量增加 f ），重复步骤 2

复杂度

(O(寻找最短路 imes maxflow))

例题 HDU-6118 度度熊的交易计划

题目链接

https://vjudge.net/problem/HDU-6118

题解

最小费用最大流，首先建立超级源点 s ，与超级汇点 t 。

因为生产一个商品需要花费 a[i] 元，且上限为 b[i] ，所以我们从 s 向这些点之间连一条容量为 b[i] ，费用为 -a[i] 的边。

同样的道理，出售一个商品可以赚到 c[i] 元，最多出售 d[i] 个，于是我们从这些点向 t 连一条容量为 d[i] ，费用为 c[i] 的边。

最后所有的公路也是花费，从 u 到 v 连接一条双向边，容量为 INF ，费用为 -k

这样使用SPFA找最长路（即获利最大）然后乘以这条路上的最大流即可

注意：图中存在自环，当我们得到两点路径长度小于 0 时应终止计算。

AC代码

#include <cstdio>
#include <vector>
#include <algorithm>
#include <iostream>
#include <queue>
#include <cstring>
#define N 550
using namespace std;
const int inf = 0x3f3f3f3f;
int n, m;
struct node {
	int u, v, cap, cost, nxt;
	node() {}
	node (int u, int v, int cap, int cost, int nxt): u(u), v(v), cap(cap), cost(cost), nxt(nxt) {}
} edge[10010];
int head[N], tot;
void init() {
	memset(head, -1, sizeof(head));
	tot = 0;
}
void adde(int u, int v, int w, int c) {
	edge[tot] = node(u, v, w, c, head[u]);
	head[u] = tot++;
	edge[tot] = node(v, u, 0, -c, head[v]);//回流费用减少
	head[v] = tot++;
}
int d[N], pre[N];
bool vis[N];
int spfa(int s, int t) {
	queue<int> q;
	memset(d, -inf, sizeof(d));
	memset(pre, -1, sizeof(pre));
	memset(vis, 0, sizeof(vis));
	d[s] = 0;
	vis[s] = 1;
	q.push(s);
	while (!q.empty()) {
		int u = q.front(); q.pop(); vis[u] = false;
		for (int i = head[u]; ~i; i = edge[i].nxt) {
			int v = edge[i].v;
			if (edge[i].cap > 0 && d[v] < d[u] + edge[i].cost) {
				d[v] = d[u] + edge[i].cost;
				pre[v] = i;
				if (!vis[v]) {
					vis[v] = true;
					q.push(v);
				}
			}
		}
	}
	return d[t] != inf;
}
int cost = 0;
void mincostmaxflow(int s, int t) {
	while (spfa(s, t)) {
		int minn = inf;
		for (int i = pre[t]; i != -1; i = pre[edge[i ^ 1].v]) {
			minn = min(minn, edge[i].cap);
		}
		for (int i = pre[t]; i != -1; i = pre[edge[i ^ 1].v]) {
			edge[i].cap -= minn;
			edge[i ^ 1].cap += minn;
		}
		if (d[t] < 0) break;
		cost += minn * d[t];
	}
}
int main() {
	while (~scanf("%d%d", &n, &m)) {
		init();
		int s = 0, t = n + 1;
		cost = 0;
		for (int i = 1; i <= n; i++) {
			int a, b, c, d;
			scanf("%d%d%d%d", &a, &b, &c, &d);
			adde(s, i, b, -a);
			adde(i, t, d, c);
		}
		for (int i = 1; i <= m; i++) {
			int u, v, c;
			scanf("%d%d%d", &u, &v, &c);
			adde(u, v, inf, -c);
			adde(v, u, inf, -c);
		}
		mincostmaxflow(s, t);
		cout << cost << endl;
	}
	return 0;
}