安全加解密引擎基础(PKE DSA)

关键词：DSA、openssl、PyCryptodome等。

1 基本概念 

DSA（Digital Signature Algorithm，数字签名算法）是用于数字签名的联邦信息处理标准。它的安全性取决于离散的对数问题。与RSA相比，DSA的签名生成速度更快，但验证速度较慢。如果使用错误的数字生成器，可能会破坏安全性。

DSA是另一种公开密钥算法，它不能用作加密，只用作数字签名。DSA使用公开密钥，为接受者验证数据的完整性和数据发送者的身份。它也可用于由第三方去确定签名和所签数据的真实性。DSA算法的安全性基于解离散对数的困难性，这类签字标准具有较大的兼容性和适用性，成为网络安全体系的基本构件之一。

1.1 DSA签名验签过程

１. 初始过程
(1) 系统参数：全局公钥KUG：p,q,g。p,q,g 作为系统参数，供所有用户使用，在系统内公开。
q: 选择素数q，位长为160，即2159<q<21602159<q<2160
p: 随机生成L位的素数p=kq+1p=kq+1，这里L在512到1024之间,且为64的倍数
g: 随机选择整数h，计算g=h(p−1)/qmod pg=h(p−1)/qmod p,其中1<h<(p−1)1<h<(p−1)，g>1g>1,gq≡1(mod p)gq≡1(mod p)
(2) 用户私钥：用户选取一个私钥x，x 随机或伪随机整数, 其中1≤x≤q−11≤x≤q−1
(3) 用户公钥：用户的公钥y，y=gxmod(p)y=gxmod(p)，公开。
与用户每条消息相关的秘密值k
k: 随机或伪随机整数, 其中0

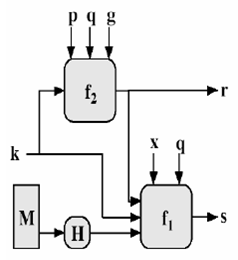
2. 签名过程
对待签消息M
输入：(（g,p,q,x),M) ， M为要签名的消息
(1) 生成一随机整数 k,0<k<q0<k<q；
(2) 计算r=(gk mod p)mod qr=(gk mod p)mod q；
(3) 计算 s=k−1(H(m)+xr)mod q。s=k−1(H(m)+xr)mod q。
则输出(r,s)(r,s)为签名人对M的签名。
注：
H(M)使用SHA-1生成的M的散列码
r不依赖消息，是k和全局公钥的函数。故对一个消息存在许多签名
离散对数的困难：从r恢复k是很困难的，从s恢复x是不可行的

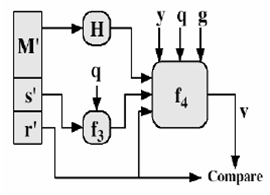
3. 验证过程
(1) 输入：((g,p,q,y),M,(r ′,s ′ ))
(2)计算w=(s')−1mod qw=(s′)−1mod q
(3) 计算u1=[H(M')w]mod q,u2=(r')wmod qu1=[H(M′)w]mod q,u2=(r′)wmod q
(4)计算v=[(gu1yu2)mod p]mod qv=[(gu1yu2)mod p]mod q
正确性证明：
验证：如 v=r ′则签名有效

其中M ′,r ′,s ′ 为接收端得到的M,r,s版本

1.2 DSA签名特点

• DSS的签名比验证快得多
• DSS不能用于加密或者密钥分配
• s⁻¹mod q要存在s ≠ 0 mod q,如果发生,接收者可拒绝该签名. 要求重新构造该签名,实际上, s ≡ 0 mod q的概率非常小
• 签名产生的计算任务有：
  • 1）计算g^kmodp求r
  • 2）确定逆元 k⁻¹求s

2 openssl关于DSA的使用

2.1 生成DSA 参数、私钥、公钥

生成DSA参数文件

openssl dsaparam -genkey 512 > dsaparam.pem

根据DSA参数文件生成DSA密钥：

openssl gendsa -out dsa.pem dsaparam.pem

打印DSA秘钥信息：

openssl dsa -in dsa.pem -text -noout

结果如下：

Private-Key: (512 bit)
priv:
    00:93:80:8e:fa:23:61:1b:a4:9b:79:fb:2d:af:17:
    77:66:54:d8:3c:74
pub: 
    00:87:60:72:d1:44:7c:15:0c:c1:6f:1a:e9:b5:67:
    73:2a:98:1f:b4:db:80:cc:e4:70:0c:00:60:f1:53:
    9a:8e:26:4e:db:fc:75:2c:c2:2c:04:46:20:30:d7:
    e9:49:c1:62:89:ee:03:57:89:21:22:5f:c9:db:18:
    41:af:64:fe:47
P:   
    00:9c:d3:70:0a:f6:7f:ac:c0:5b:46:6b:f9:c2:e4:
    b7:59:7b:23:31:7e:00:3a:2b:d6:2b:94:5d:db:80:
    97:0a:d7:fc:2d:ef:82:44:07:08:75:37:c1:fa:b6:
    43:a6:e6:9e:fc:2d:7b:8c:dc:8e:0d:fc:99:f4:9c:
    4d:6b:18:29:9f
Q:   
    00:c7:7e:4b:4e:92:69:25:65:39:ba:a3:01:79:3c:
    42:88:ae:0e:9e:6f
G:   
    2a:72:1d:12:fa:c7:f9:50:77:3b:be:1e:75:18:9e:
    77:13:59:01:68:c7:a7:54:4f:7a:00:35:bb:f7:cf:
    0c:79:fa:f0:9e:a7:c1:95:c6:1e:b7:87:d4:1e:7e:
    fb:20:ee:5c:39:d5:94:c4:b7:75:6d:29:01:e5:ae:
    eb:70:aa:d3

 从私钥中提取公钥：

openssl  dsa -in dsa.pem -out pubdsa.pem -pubout

2.2 使用DSA进行签名和验签

使用私钥dsa.pem对sample.txt进行签名，结果存入sample.sign：

openssl dgst -sha256 -sign dsa.pem -out sample.sign sample.txt 

使用sample.sign对sample.txt进行验签：

openssl dgst -sha256 -verify pubdsa.pem -signature sample.sign sample.txt 

3 Python关于DSA的使用

Python使用PyCryptodome进行DSA签名和验签：

from Crypto.PublicKey import DSA
from Crypto.Signature import DSS
from Crypto.Hash import SHA256

if __name__ == '__main__':

     # Create a new DSA key
    key = DSA.generate(2048)
    publickey = key.publickey().export_key()
    with open("public_key.pem", "wb") as f:
        f.write(publickey)
    f.close()

    privatekey = key.export_key()
    with open("private_key.pem", 'wb') as f:
        f.write(privatekey)
    f.close()
     # Sign a message
    message = b"This is a sample."
    hash_obj = SHA256.new(message)
    signer = DSS.new(key, 'fips-186-3')
    signature = signer.sign(hash_obj)

    # Load the public key
    with open("public_key.pem", "r") as f:
        pub_key = DSA.import_key(f.read())
        verifier = DSS.new(pub_key, 'fips-186-3')

        # Verify the authenticity of the message
        try:
            verifier.verify(hash_obj, signature)
            print("The message is authentic.")
        except ValueError:
            print("The message is not authentic.")
    f.close()

 更多参考：

《DSA数字签名原理及python实现》-DSA签名原理、签名特点、签名实例介绍。

《DSA — PyCryptodome 3.14.1 documentation》-PyCryptodome关于DSA API介绍以及使用方法。