T1

思路
容斥原理
主要是处理3 4 5....个数字的lcm时出了问题
由于一开始容斥原理用错了,求的是乘积(乘积只针对互质的数,而此题数据显然没有限制)
对拍发现错误样例后,在a[i]中删除了一个数是另一个数的整倍数的情况
然后就为下文怎么改也改不出来做了铺垫
正确的解法应该是俩俩求lcm
如a:6 9 5 7
6 9 5的lcm:
lcm((6,9),5)=lcm(18,5)=90
#include<iostream> #include<cstring> #include<cstdio> using namespace std; int n,m; int a[25]; bool chosen[25]; long long tot[25]; inline int findgcd(int x,int y){ return !y?x:findgcd(y,x%y); } //now:已选个数,x:总共选择个数,mul:目前乘积 void work(int now,int x,long long mul,int maxx){ if(mul>(long long)n) return; if(now==x){ tot[x]+=n/mul; return; } for(int i=maxx+1;i<=m;i++){ if(!chosen[i]){ int gcd=findgcd(mul,a[i]); long long ret=mul/gcd*a[i]; chosen[i]=true; work(now+1,x,ret,i); chosen[i]=false; } } } int main(){ freopen("count.in","r",stdin); freopen("count.out","w",stdout); scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) scanf("%d",&a[i]); long long answer=0; for(int i=1;i<=m;i++){ work(0,i,1,0); } for(int i=1;i<=m;i++){ if(i%2) answer+=tot[i]; else answer-=tot[i]; } answer=n-answer; cout<<answer<<endl; return 0; }
T2
思路
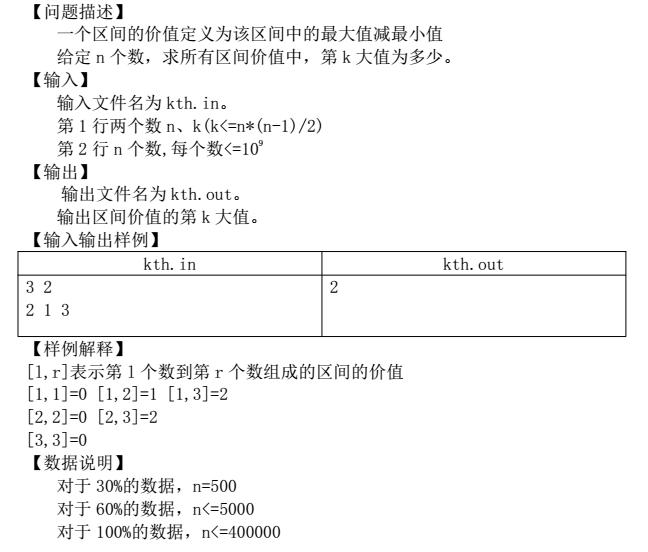
二分第k大值
Check(int kk):判断当前价值比mid大的区间是不是比k个多
“对于每个固定的右端点,它左侧一定存在一个阀值ki使l<=ki[l,r]的价值必定大于等于ans
且随i增大,ki单调不降”
摘自某题解,我确实想不到比这更准确又更简洁的描述方式了
通俗讲,就是一旦右端点i固定了,在它左侧就会存在一个点x,使得同样以i为右端点、比[x,i]长的区间的价值比[x,i]大,而且,i变大,ki不会变小,要么不变,要么跟着变大
关于单调队列应用:
q1[i]:a[i]后面第一个比a[i]大的数的位置
q2[i]:a[i]后面第一个比a[i]小的数的位置
#include<iostream> #include<cstring> #include<cstdio> using namespace std; #define N 400005 long long a[N],q1[N],q2[N]; long long k; long long n; void read(long long &now){ now=0;bool flag=false; char c=getchar(); while(c<'0'||c>'9'){ if(c=='-')flag=true; c=getchar(); } while(c>='0'&&c<= '9'){ now=now*10+c-'0'; c=getchar(); } now=flag?-now:now; } bool check(int kk){ int l1=1,r1=1,l2=1,r2=1; q1[1]=1;q2[1]=1; int z=1; long long ans=0; if(kk==1)ans=1; else ans=0; for(int i=2;i<=n;i++){ while(l1<=r1 && a[q1[r1]]>=a[i]) r1--; q1[++r1]=i; while(l2<=r2 && a[q2[r2]]<=a[i]) r2--; q2[++r2]=i; while(z<i){ int t1=l1,t2=l2;z++; while(q1[t1]<z) t1++; while(q2[t2]<z) t2++; if(a[q2[t2]]-a[q1[t1]]>=kk){ l1=t1;l2=t2; }else{ Z--;break; } } if(a[q2[l2]]-a[q1[l1]]>=kk) ans+=z; } return ans>=k; } int main(){ freopen("kth.in","r",stdin); freopen("kth.out","w",stdout); read(n);read(k); for(int i=1;i<=n;i++)read(a[i]); int l=0,r=1000000000; while(l<r){ int mid=(l+r+1)/2; if(check(mid))l=mid; else r=mid-1; } cout<<l<<endl; return 0; }
T3

思路
当时,写是最暴力的暴力
正解:
选定几个武器使其不被摧毁,对是否可能进行判断:
按照攻击力从小到大排序,要保证其不被摧毁
则后面的r个都是比它攻击力小的
如果找不够,那就不可能
所以,总结判断方法:
攻击力第i小的选定武器,其攻击力在所有武器中排名需>=i*(r+1)
按照攻击力从小到大将武器排序
dp[i][j]:前j个武器选了i个且可能成立的最大贡献
#include<algorithm> #include<iostream> #include<cstring> #include<cstdio> #define N 5005 #define INF 1000000000 using namespace std; int dp[N/2][N],n,r; struct node{ int x,y; friend bool operator < (node a,node b){ return a.x<b.x; } }q[N]; int main(){ freopen("submax.in","r",stdin); freopen("submax.out","w",stdout); int T;scanf("%d",&T); while(T--){ scanf("%d%d",&n,&r); for(int i=1;i<=n;i++) scanf("%d",&q[i].x); for(int i=1;i<=n;i++) scanf("%d",&q[i].y); sort(q+1,q+n+1); int m=n/(1+r)+((n%(1+r))>0); int ans=0; for(int i=1;i<=m;i++){ int tt=min((1+r)*i,n); for(int j=0;j<tt;j++) dp[i][j]=-INF; for(int j=tt;j<=n;j++) dp[i][j]=q[j].y+dp[i-1][j-1]; for(int j=1;j<=n;j++) dp[i][j]=max(dp[i][j],dp[i][j-1]); ans=max(ans,dp[i][n]); } printf("%d ",ans); } return 0; }