https://www.cnblogs.com/skywang12345/p/3638342.html
https://blog.csdn.net/wang3312362136/article/details/80615874
要维护一段区间内的最值时,我们可以用堆(平衡树)来操作。
但是,如果要合并两个堆,复杂度就极高了。
所以,我们就要使用左偏树这个神奇的数据结构,来实现堆的合并。
左偏树是什么?
当然是向左偏的树。(废话)
实际上,现在来解释左偏树的概念还是有点难的,所以我们要先来看一些定义。
与左偏树相关的一些定义
外节点
外节点,顾名思义,就是在外部的节点。
它的定义是有至少一个子节点是空节点的节点是外节点。
注意是至少一个,而不是全部,不然就变成叶节点了。
而记录外节点有什么用呢?
当我们需要插入一个节点时,如果找到了外节点,就可以轻松将其插入到这个外节点的某一空子节点。
距离
左偏树一个很重要的概念就是节点的距离,我们可以将其记作Dis(x)Dis(x)。
比较简单,一个节点的距离指的就是它到离它最近的外节点的距离。
对于该节点本身是外节点和该节点是空节点两种特殊情况,我们分别规定它们的距离为0和−1。
左偏树的一些性质
首先,我们要知道,左偏树是满足堆性质的(废话,它就是用来实现堆合并的)。
而左偏树另一比较重要的性质是左偏性。
让我们回到前面的那个问题,什么是左偏树?
现在我们可以对它进行解释了:对于左偏树中的任意一个节点,我们必须满足Dis(LeftSon)≥Dis(RightSon),即左儿子离外节点的距离必须大于等于右儿子离外节点的距离。
而这就是左偏树的左偏性了。
左偏树其实还有一个比较重要的性质,这个性质在上传信息的操作中起到了重要的作用:对于左偏树中的任意一个节点,Dis(x)=Dis(RightSon)+1。
证明: 根据左偏性,可以得到Dis(RightSon)≤Dis(LeftSon),而左偏树中距离的定义是一个节点到离其最近的外节点的距离,故为Dis(RightSon)+1。
一、左偏树的性质
左偏树,又称可并堆,所以他有堆的性质。
定义几个量:valval表示该节点的值,fafa表示该节点的父亲,ch[2]ch[2]表示该节点的两个儿子(因为他是二叉树),disdis表示这个节点到离他最近的叶子节点的距离。
性质一:该节点的val不大于该节点左右儿子的val
证明:堆。
性质二:该节点左儿子的dis不小于该节点右儿子的dis
证明:左偏树的定义。为了更快的进行合并、查询、删除(快速提取最小值)。
性质三:该节点的dis等于该节点右儿子的dis。
证明:构造的。
性质四:一棵n个节点的左偏树的节点的距离k最多为log(n+1)−1log(n+1)−1
证明:因为左偏树是一棵二叉树,当他节点最少的时候他是一棵完全二叉树,所以n>=2(k+1)−1n>=2(k+1)−1,那么k<=log(n+1)−1k<=log(n+1)−1。(这个结论是用来证明左偏树的时间复杂度的)
二、左偏树的主要操作
左偏树的主要实现就是他的merge,我们删除,插入一个节点就是利用左偏树的merge函数进行操作的。
merge函数的实现方法:
首先,我们建出来的左偏树是一定要符合以上四个性质的,所以我们的merge就是为了在合并后,左偏树仍有这些性质。
1.我们要保证性质一
所以:
if(val[x]>val[y]||(val[x]==val[y]&&x>y)){//性质一
swap(x,y);
}
2.我们要开始合并,我们将以节点y形成的左偏树和节点x的右子树合并,在让合并后所形成的的左偏树满足性质。
ch[x][1]=merge(ch[x][1],y);//合并右子树和y
3.合并后的左偏树要满足性质三
dis[x]=dis[ch[x][1]]+1;//性质三
4.我们要更新节点的fa
fa[x]=fa[ch[x][0]]=fa[ch[x][1]]=x;//更新fa
5.为了操作4,我们要return 根节点
return x;
综上,merge函数就是:
int merge(int x,int y){
if(!x||!y){
return x+y;
}
if(val[x]>val[y]||(val[x]==val[y]&&x>y)){//性质一
swap(x,y);
}
ch[x][1]=merge(ch[x][1],y);//合并右子树和y
if(dis[ch[x][0]]<dis[ch[x][1]]){//性质二
swap(ch[x][0],ch[x][1]);
}
fa[x]=fa[ch[x][0]]=fa[ch[x][1]]=x;//更新fa
dis[x]=dis[ch[x][1]]+1;//性质三
return x;
}
三、基于merge函数的操作
删除某一节点(pop)
我们只要合并这个节点的左右儿子即可。
void pop(int x){
val[x]=-1;
fa[ch[x][0]]=ch[x][0];
fa[ch[x][1]]=ch[x][1];
fa[x]=merge(ch[x][0],ch[x][1]);
}
求某一节点所在堆得最小值,并删除此节点
xx=getfa(x);
printf("%d
",val[xx]);
pop(xx);
另:
有关getfa:
一定要路径压缩,不然原来O(logn)O(logn)的查询,就会被一条链卡成O(n)O(n)。
在学OI的前期,我们接触了一种数据结构,叫做堆。它资瓷插入一个元素,查询最小/大元素和删除最小/大元素。然后就发现STL的priority queuepriority queue可以直接用,非常的方便。
但是有时候题目让我们资瓷两个堆的合并,这样priority queuepriority queue就不行了(但是pb_ds还是可以的)。这样我们就要手写左偏树。
什么是左偏树呢?首先,从名字上看,它是一棵树。其实它还是一棵二叉树。它的节点上存4个值:左、右子树的地址,权值,距离。
权值就是堆里面的值。距离表示这个节点到它子树里面最近的叶子节点的距离。叶子节点距离为0。
既然是一种特殊的数据结构,那肯定有它自己的性质。左偏树有几个性质(小根为例)。
性质一:节点的权值小于等于它左右儿子的权值。
堆的性质,很好理解。
性质二:节点的左儿子的距离不小于右儿子的距离。
在写平衡树的时候,我们是确保它的深度尽量的小,这样访问每个节点都很快。但是左偏树不需要这样,它的目的是快速提取最小节点和快速合并。所以它并不平衡,而且向左偏。但是距离和深度不一样,左偏树并不意味着左子树的节点数或是深度一定大于右子树。
性质三:节点的距离等于右儿子的距离+1。
没什么好说的= =
性质四:一个n个节点的左偏树距离最大为log(n+1)-1log(n+1)−1
这个怎么证明呢?我们可以一点一点来。
若左偏树的距离为一定值,则节点数最少的左偏树是完全二叉树。
节点最少的话,就是左右儿子距离一样,这就是完全二叉树了。
若一棵左偏树的距离为k,则这棵左偏树至少有2^{k+1}-12k+1−1个节点。
距离为k的完全二叉树高度也是k,节点数就是2^{k+1}-12k+1−1。
这样就可以证明性质四了。因为n>=2^{k+1}-1,所以k<=log(n+1)-1
有了性质,我们来讲讲它的操作。
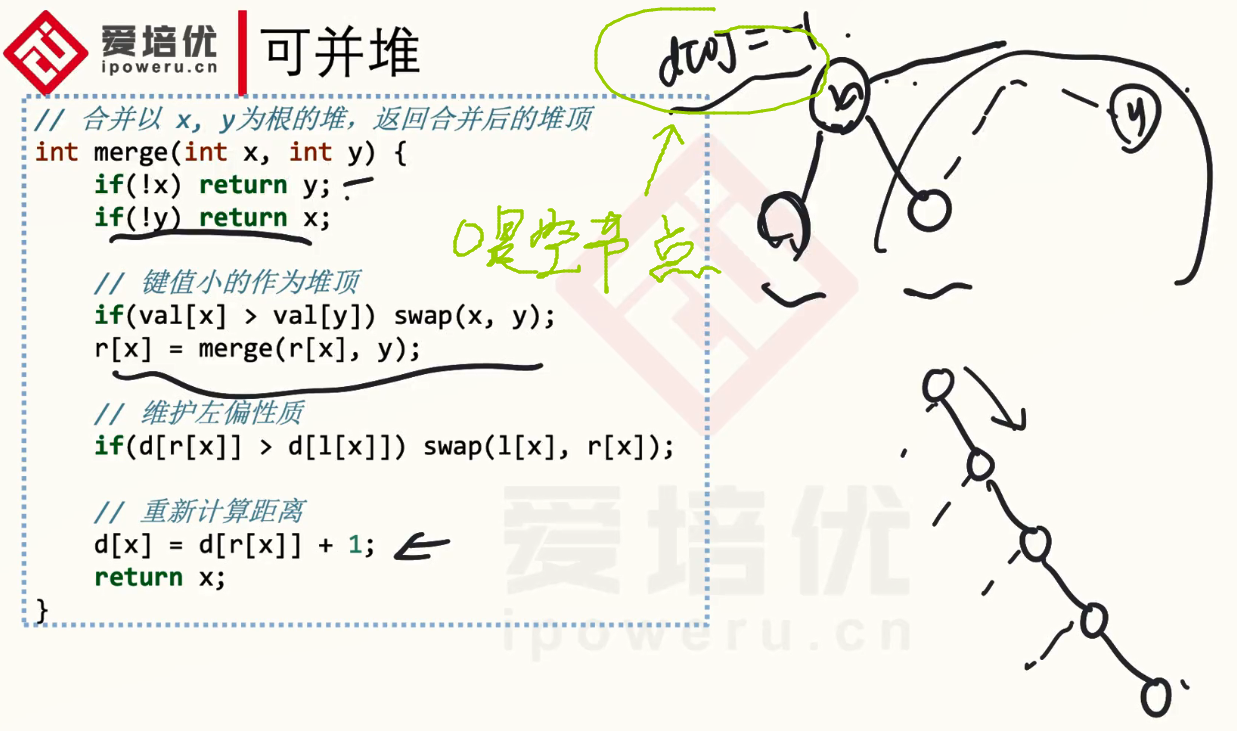
1.合并
<center></center>
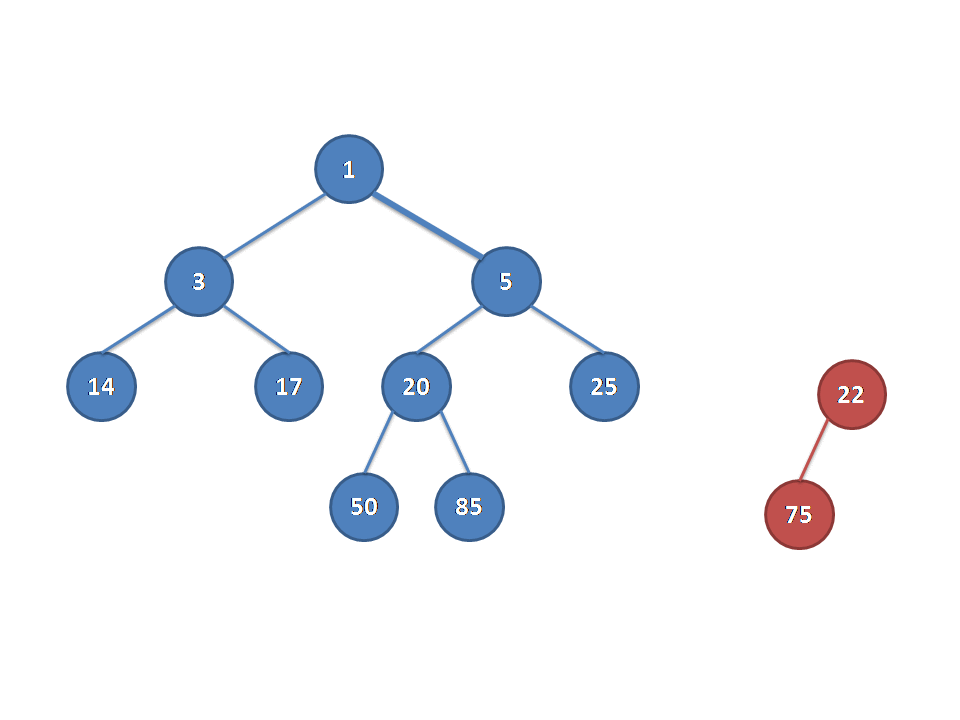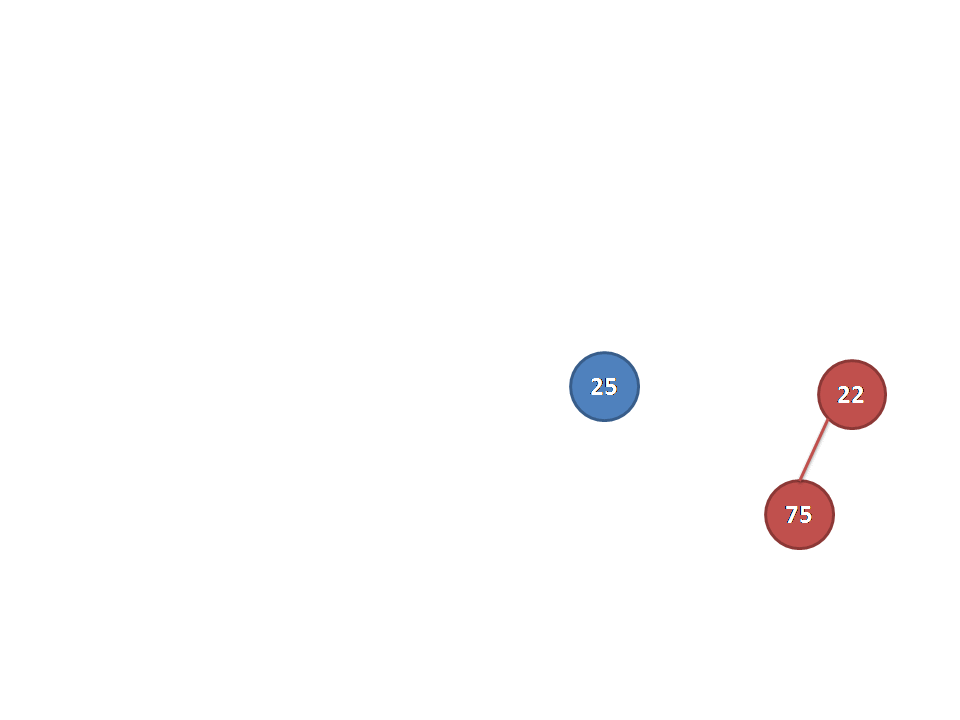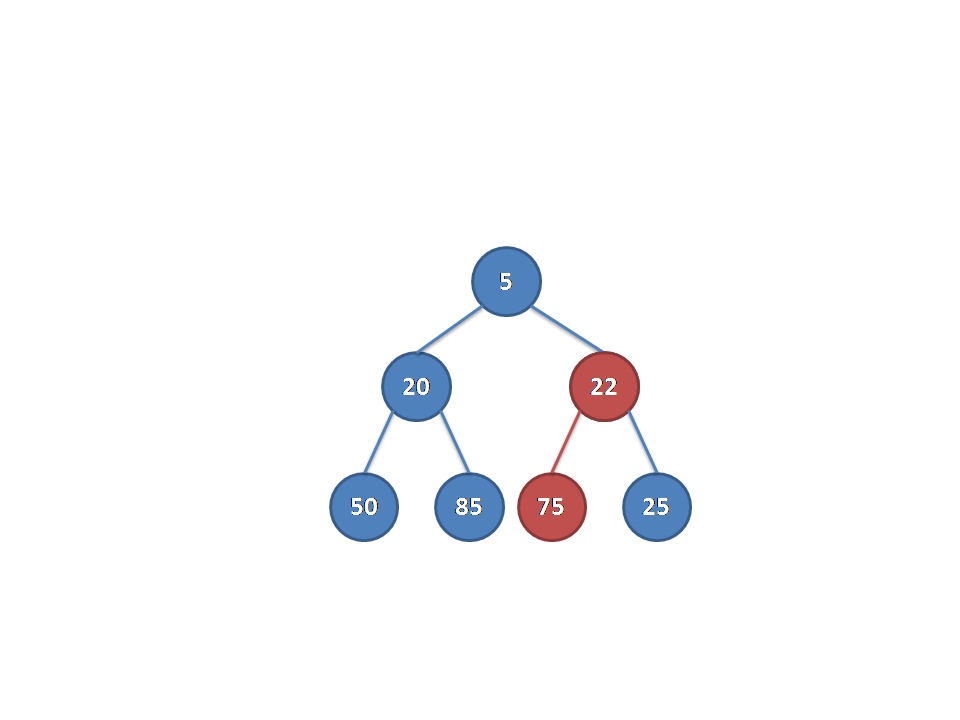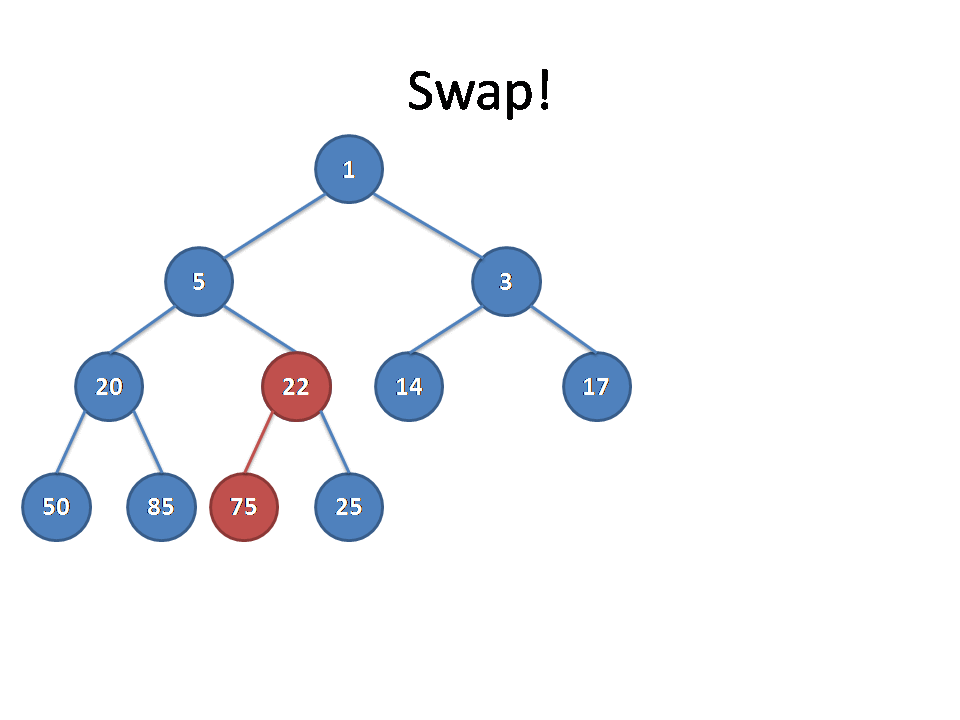
我们假设A的根节点小于等于B的根节点(否则交换A,B),把A的根节点作为新树C的根节点,剩下的事就是合并A的右子树和B了。
<center></center>
合并了A的右子树和B之后,A的右子树的距离可能会变大,当A的右子树 的距离大于A的左子树的距离时,性质二会被破坏。在这种情况下,我们只须要交换A的右子树和左子树。
而且因为A的右子树的距离可能会变,所以要更新A的距离=右儿子距离+1。这样就合并完了。
<center>
int merge(int x,int y){
if (x==0 || y==0)
return x+y;
if (val[x]>val[y] || (val[x]==val[y] && x>y))
swap(x,y);
ch[x][1]=merge(ch[x][1],y);
f[ch[x][1]]=x;
if (dis[ch[x][0]]<dis[ch[x][1]])
swap(ch[x][0],ch[x][1]);
dis[x]=dis[ch[x][1]]+1;
return x;
}
我们来分析一下复杂度。我们可以看出每次我们都把它的右子树放下去合并。因为一棵树的距离取决于它右子树的距离(性质三),所以拆开的过程不会超过它的距离。根据性质四,不会超过log(n_x+1)+log(n_y+1)-2,复杂度就是O(log n_x+log n_y)
2.插入
插入一个节点,就是把一个点和一棵树合并起来。
因为其中一棵树只有一个节点,所以插入的效率是O(log n)
3.删除最小/大点
因为根是最小/大点,所以可以直接把根的两个儿子合并起来。
因为只合并了一次,所以效率也是O(log n)
左偏树模板呀
// ①:空节点为-1(性质推得)
// ②:删除操作:将其左右子树合并,接上去即可
// 插入操作:将插入的点用倍增合成一树,插入即可
// 替换操作:先删除再插入(注意删除时d[x]=r[x]=v[x]=l[x]=0)
#include<bits/stdc++.h>
#define Int register int
#define N 100005
using namespace std;
int n,m;
int fa[N],son[N][2],dead[N],dist[N],val[N];
int read (int &x){
x = 0;
char c = getchar();
int f = 1;
while(c < '0' || c > '9') {if (c == '-') f = -f;c = getchar();}
while(c >= '0' && c <= '9') {x = (x << 3) + (x << 1) + c - '0';c = getchar();}
return x*f;
}
void write (int x){
if(x < 0) {x = -x;putchar ('-');}
if(x > 9) write (x / 10);
putchar (x % 10 + '0');
}
int findSet (int x){
if (x != fa[x])
fa[x] = findSet (fa[x]);
return fa[x];
}
int Merge (int x,int y){
if (!x || !y)
return x | y;
//if(x==0) return y; //只剩某一子数(点)的情况
//if(y==0) return x;
//判断到尽头,儿子为空要返回对应的另一结点
if (val[x] > val[y] )
swap (x,y);
//如果值x大于y 或者值相同情况下 x的位置在y右边 交换
son[x][1] = Merge (son[x][1],y);
//将y不断地和x的右儿子进行合并
//将合并后的新的右儿子的父亲边连上
dist[x] = dist[son[x][1]] + 1;
//fa[lson[x]]=fa[rson[x]]=fa[x]=x;
//如果右儿子的dis要大于左儿子 进行交换
//dis[x]=(rson[x]==0?0:dis[rson[x]]+1);
//x的dis为其右儿子的dis+1
//若无右儿子则dis为0
if (dist[x] > dist[son[x][0]] + 1)
swap (son[x][0],son[x][1]);
fa[son[x][0]] = fa[son[x][1]] = fa[x] = x;
return x;
}
int Ask (int x){
dead[x] = 1;
int tmp = val[x];
fa[son[x][0]] = son[x][0];
fa[son[x][1]] = son[x][1];
fa[x] = Merge (son[x][0],son[x][1]);
return tmp;
}
signed main(){
read(n),read(m);
for (Int i = 1;i <= n;++ i)
fa[i] = i,read (val[i]);
for (Int i = 1;i <= m;++ i) {
int opt;
read (opt);
if(opt == 1){
int x,y;
read (x),read (y);
if (dead[x] || dead[y]) continue;
x = findSet (x),y = findSet (y);
if (x != y)
fa[x] = fa[y] = Merge (x,y);
} else if(opt == 2){
int x;
read (x);
if(dead[x]) puts ("-1");
else write (Ask (findSet (x))),putchar ('
');
}
}
}

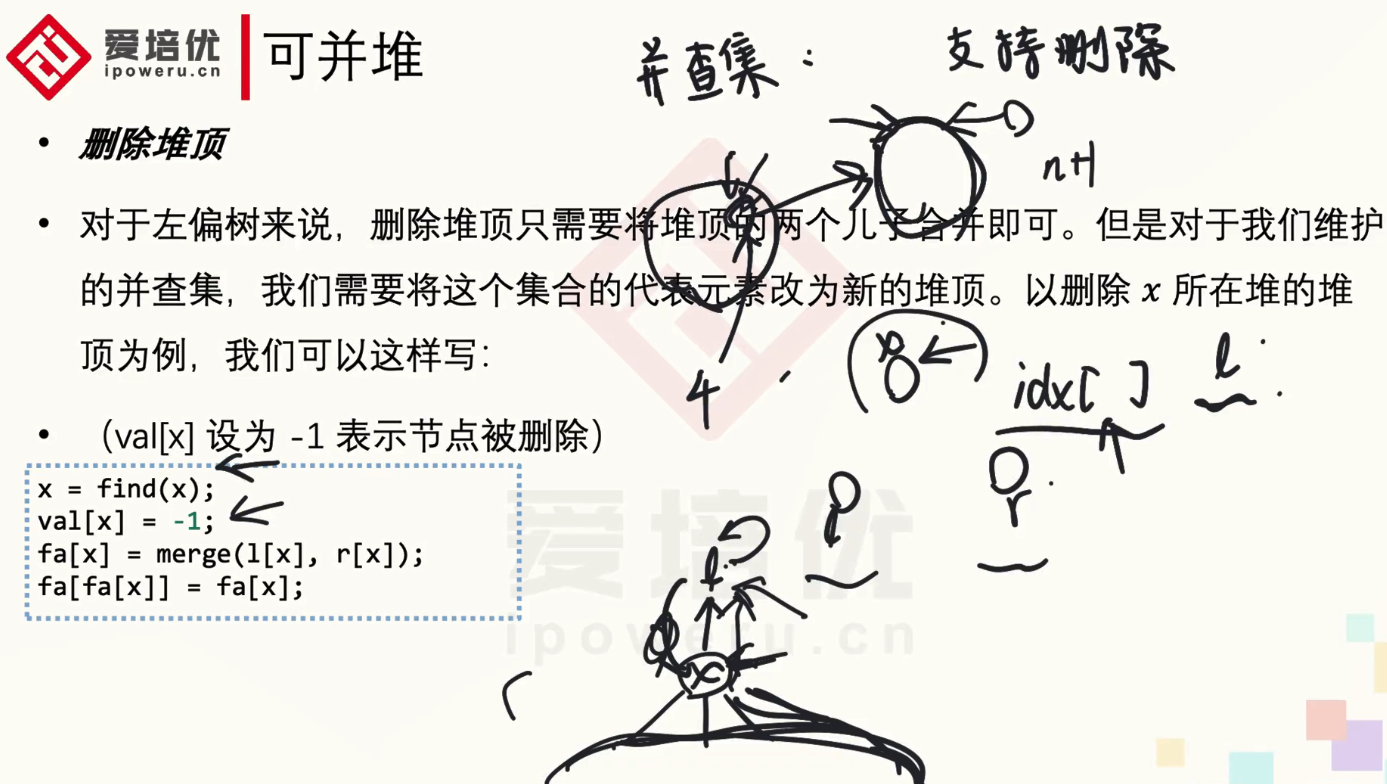
x虽然被删除了,但还是有用的
数组idx[ ]表示现在的这个点被换成了哪个点
索引导他现在真正存在的那个点
所以就能实现删除了,就支持把一个元素从一个集合中拿到另一个集合中了


join可以把两个堆合并起来

