数据结构复习
模式匹配
模式匹配就是给定模式串和主串,在主串中找模式串第一次出现的位置的算法。
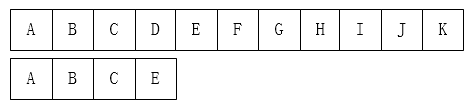
BF算法
BF算法就是暴力匹配算法,下面给个简单代码就过吧。
char* s1 = "abcaba";//主串
char* s2= "aba";//模式串
int i=0;//主串中的位置
int j=0;//模式串中的位置
while(i<strlen(s1)&&j<strlen(s2)){//防止越界
if(s1[i]==s2[j]){//匹配成功则比较下一位
i++;
j++;
}else{
i=i-j+1;//匹配失败,i回退
j=0;//j从0开始匹配
}
}
if(j>strlen(s2)){
cout<<i-j<<endl;//找到了输出位置
}else{
cout<<-1<<endl;//没找到输出-1
}
KMP算法
上面的暴力算法回退的太多,很多无用的比较,浪费时间,KMP算法解决了这个问题,提出了next数组,使得在一次比较失败之后可以快速跳过无用比较,大大简化了算法。其思路是主串的i每次不回退,j不一定回退到0,而是按照next数组回退到对应的位置,那么关键就是next数组的计算了。
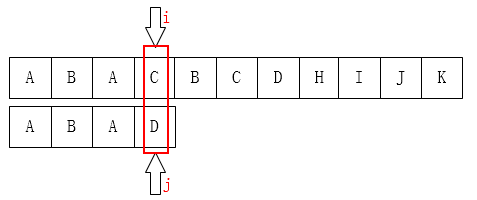
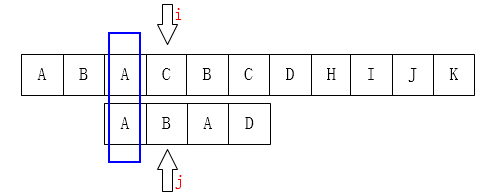
next数组
next数组存在的意义是为了简化j的回退,方便理解而言,提出了最长公共前后缀的概念,但实际代码中并不体现这种理解。
例如,对于字符串“abcsab”的前缀串集合为{a,ab,abc,abcs,abcsa},后缀串集合为{b,ab,sab,csab,bcsab},可以看出最大公共前后缀字串为ab。长度为2,因此对应next数组值就是2。
求解代码:
void get_next(char* s,int* next){
next[0] = -1;
next[1] = 0;
int k = 0;//初始位置next值
int i = 2;//初始需要赋值的位置
while(i<strlen(s)){
if(k==-1||s[i-1]==s[k]){//如果相等,next的值就是当前位置next的值+1
next[i++] = ++k;
}else{
k = next[k];//不相等则继续往前找,直到k=-1或者找到相等的
}
}
}
模式匹配代码:
int KMP(char* m,char* s,int pos){//pos是指从pos位置开始匹配
int i=pos;
int j=0;
int* next = new int[strlen(s)];
get_next(s,next);
while(i<strlen(m) && j<strlen(s)){
if(j==-1 || m[i]==s[j]){
j++;
i++;
}else{
j = next[j];//直接按照next数组进行回退
}
}
delete next;
if(j>=strlen(s)){
return i-j;
}else{
return -1;
}
}
改进的KMP算法
上面的KMP算法存在的问题是,如果模式串为"aaaaaaaab",那么其next数组的值便是[-1,0,1,2,3,4,5,6,7],也就意味着,如果最后一个a不匹配,那么将一步一步回退j,回退了之后进行重复的比较,继续回退(因为还是a,还是失配)。所以我们如果能判断s[i]是否与s[k]相等,如果相等,其next值直接为next[k]就好了。所以改进后的next数组值应该为[-1,-1,-1,-1,-1,-1,-1,-1,0],简单来说,就是在之前next数组的基础上呢,看要跳转到的地方的字符跟当前扫描到的字符是否相等,相等直接就让当前的next值为跳转地方的next值,因为就算跳过去也还会进行同样的比较,多余的比较。
改进的next求解代码
int* get_next_plus(char* s,int* next){
next[0] = -1;
int i=0;
int k=-1;
while(i<strlen(s)){
if(k==-1 || s[i]==s[k]){
i++;
k++;
if(i>=strlen(s)){
break;
}
if(s[i]==s[k]){
next[i] = next[k];
}else{
next[i] = k;
}
}else{
k = next[k];
}
}
}
后缀表达式求值
过程:
- 遍历表达式,遇到数字入栈
- 遇到操作数,弹出最上面的两个元素,执行操作,操作完后结果再入栈
- 一直读完,将最后的结果输出
例子:
32 26 - 5 * 28 4 / +
32-26=6
6*5=30
28/4=7
30+7=37
结果就是37
中缀表达式转后缀表达式
下面规则用来理解转换过程,理解扫描过程栈变化的情况。
中缀表达式a + b*c + (d * e + f) * g,其转换成后缀表达式则为a b c * + d e * f + g * +。
转换过程需要用到栈,具体过程如下:
1)如果遇到操作数,我们就直接将其输出。
2)如果遇到操作符,则我们将其放入到栈中,遇到左括号时我们也将其放入栈中。
3)如果遇到一个右括号,则将栈元素弹出,将弹出的操作符输出直到遇到左括号为止。注意,左括号只弹出并不输出。
4)如果遇到任何其他的操作符,如(“+”, “*”,“(”)等,从栈中弹出元素直到遇到发现更低优先级的元素(或者栈为空)为止。弹出完这些元素后,才将遇到的操作符压入到栈中。有一点需要注意,只有在遇到" ) "的情况下我们才弹出" ( ",其他情况我们都不会弹出" ( "。
5)如果我们读到了输入的末尾,则将栈中所有元素依次弹出。
静态链表
静态链表是用数组来模拟存储空间实现链表的。
分为head链和avail链,head链存储的是具体数据,而avail链存储的是可利用空间。
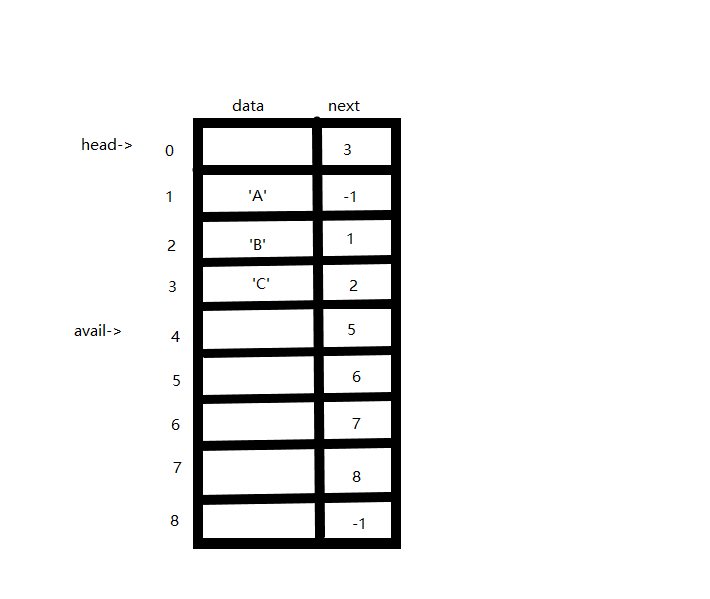
读一下:
'C'、'B'、'A'
如果要添加数据,就要从可以用空间开始添加,删除的修改avail指针就可以了,不需要把值改掉。
循环队列
//循环队列判空条件:
rear==front;
//循环队列判满条件:
(rear+1)%maxSize == front;
//求循环队列的长度:
(rear-front+maxSize)%maxSize;
//遍历循环队列
for(i=front;i!=rear;i=(i+1)%maxSize)
栈、队列和递归单元 - 易错题
判断题
- 栈是操作受限的线性表,它只允许在表头插入和删除元素。(x)- 栈只允许在表尾插入和删除元素,所以错。
- 只有使用了局部变量的递归过程在转换成非递归过程时,才必须使用栈。 (x) - 是否必须使用栈和局部变量存在与否无关,尾递归形式可以不用栈模拟,而递归过程中函数的调用取地址等操作必须由栈模拟(除尾递归等特殊情况)。
填空题
-
有n个数入栈,则出栈的顺序有C(2n,n)-C(2n,n-1)种;卡特兰数的定义:
令h(0)=1,h(1)=1,Catalan数满足递归式:h(n) = h(0)*h(n-1) + h(1)*h(n-2) + ... + h(n-1)*h(0) (n>=2),
-
在双端队列中,元素进入该队列的顺序依次为a,b,c,d,则既不能由输入受限的双端队列得到,又不能由输出受限的双端队列得到的输出序列是dbca;分析:输入受限的双端队列可以看成是一个队列和一个栈的组合,因此如果队列和栈都无法输出的元素在输入受限的双端队列中同样无法输出。而我们知道,栈可以输出的组合个数为C(8,4)-C(8,3) = 14种,队列能输出的组合个数为1种,四个元素排列有A(4,4)=24种,24-14-1=9种,所以两种结构都不能输出的组合数共有9种。只考虑栈不能输出的组合,因为数目小。分别为adbc,bdac,cabd,cadb,dabc,dacb,dbac,dbca,dcab,在这几个序列里面找输出受限的队列不能输出的序列,就很容易找到dbca了。
数组的存储结构
二维数组的顺序存储结构分为以行序为主序的存储方式和以列序为主序的存储方式。
以行序为主的存储方式就是常规的先存第0行的每列,再存第一行的每列,以此类推。以列为主的存储方式同理。
对于三维数组来说,按下标从左到右的顺序存储。例如,设a[0][0][0]的地址为p,则对于数组a[m][n][r],a[i][j][k] = p + (i*n*r + j*r + k)*l;
稀疏矩阵
三元组顺序表
转置函数最简单的方法就是row和col对应的值交换,并且row和col顺序交换,然后按照行从小到大排序。
O(col*num)的转置算法:
把M矩阵的第0列的所有元素找出来,转置,放到N矩阵的第0行,把M矩阵的第1列所有元素找出来,转置,放到N矩阵的第1行,以此类推。每次照完所有第n列元素需要扫描col次,转置num个元素,时间复杂度O(col*num)。
int i=0;
for(int col=0;col<cols;col++){//找每一列的所有元素
for(int j=0;j<num;j++){
if(triElems[j].col == col){//找到了之后存到N的第j行
N.triElems[i].row = triElems[j].col;
N.triElems[i].col = triElems[j].col;
N.triElems[i].val = triElems[j].val;
i++;
}
}
}
O(num)算法:
空间换时间,申请两个数组,一个用来记录每一列的第一个非0元存储的起始位置,另一个用来存储这一列有多少个非0元。因为在原矩阵的三元组表示种,存储是连续的,一旦我们知道了某一列存储的非0元起始地址和长度(相当于知道了终止地址),我们就能确定整个一列,进而转置整个一行。下面简要写一下。
int *cNum = new int[col+1];//存储每一列非0元个数
int *cPos = new int[col+1];//存储每一列第一个非0元起始位置
for(int col=0;col<cols;col++) cNum[col] = 0;
for(int i=0;i<nums;i++) cNum[triElems[i].col]++;
cPos[0] = 0;
for(int col=1;col<cols;col++){//下一列第一个非0元的起始位置=上一列非0元的起始位置 + 上一列非0元个数
cPos[col] = cPos[col-1] + cNum[col-1];
//我觉得这里很巧妙
}
//由于是从小列到大列求的非0元起始位置,所以的时候的存储顺序就是M矩阵按列从小到大存储的
//上面就都求完了,直接开始转置
for(int i=0;i<nums;i++){
int j=cPos[triElems[i].col];//得到的是M矩阵存储的第i个元素的col列的起始非0元位置
N.triElems[j].row = triElems[i].col;
N.triElems[j].col = triElems[i].row;
N.triElems[j].row = triElems[i].val;
cPos[triElems[i].col]++;
//注意这里是重点,非常巧妙的++,这样下一次循环进来找到的非0元起始位置就是之前位置+1,不用再写个循环了
}
广义表
定义相关
LS=(a1,a2,...,an)
LS是表名,表的长度为n,长度为0的广义表为空表。如果n>=1,则a1是表头,(a2,a3,...,an)是表尾。(注意表头没有加括号表示是原子,而表尾加括号了表示子表)
广义表种括号的重数代表广义表的深度。递归表的深度为无穷大。
表头、表尾
一个例子足以
A = ((),(a,b,c),d,e)
head(A) = ()
tail(A) = ((a,b,c),d,e)
取到c的操作是head(tail(tail(head(tail(A)))))
画存储结构
广义表的存储结构为:
tag- data/slink-link
tag=1,为原子; tag =0, 为子表.
data--为原子数据,slink---为子表地址
link---为本元素的同层下一个元素的地址
A = ((),a,(b,(c,d)),(e,f))

树的相关概念
节点的度:一个节点的子树数目成为节点的度。也就是一个节点连着几个子节点的意思。
叶子节点:没有子节点的节点。
树的度:Max{所有节点的度}。
深度:就是树的高度,很好理解不解释。
二叉树的相关概念
- 有n个节点的二叉树的分支数为n-1
- 若二叉树高为h,则该二叉树最少有h个节点,最多有2^h-1个节点
- 若高度为h的二叉树具有最大数目的节点,则称其为满二叉树
- 若高度为h的二叉树除第h层外,其他各层的节点数都达到最大个数,并且第h层的节点还是连续分布的,则称其为完全二叉树。
- 具有n各节点的完全二叉树高度为log2 (n+1)取上界。
二叉树的遍历
递归算法
前序遍历
void preOrder(Node* r){
if(!r){//递归终点
return;
}
cout<<r->data;//先输出
preOrder(r->left);//再递归左子树
preOrder(r->right);//再递归右子树
}
中序遍历
void inOrder(Node* r){
if(!r){//递归终点
return;
}
inOrder(r->left);//先递归左子树
cout<<r->data;//再输出
inOrder(r->right);//再递归右子树
}
后序遍历
void postOrder(Node* r){
if(!r){
return ;
}
postOrder(r->left);//先递归左子树
postOrder(r->right);//再递归右子树
cout<<r->data;//最后输出
}
层次遍历
void Level(Node* r){
queue<Node*> q;
if(!r){
return;
}
Node* p;
q.push(r);
while(!q.empty()){
p = q.front();//取出元素
cout<<p->data;//访问
q.pop();//出队
if(p->left){
q.push(p->left);
}
if(p->right){
q.push(p->right);
}//由于是按照先左后右的顺序入队的,出队的顺序在同一层里也是先左后右
//因此实现了层次遍历
}
}
非递归算法
栈可以实现非递归的二叉树三种遍历,实际上栈的作用是存储访问的顺序,这样就不需要再回溯找,直接能够通过取出栈顶元素得到下一个应该被访问的节点。
前序遍历
用栈:
void preOrder(Node* r){
stack<Node*> s;
Node* p = r;
while(!s.empty() || p){
while(p){//如果p不为NULL,就一直往左遍历,边遍历边输出。
cout<<p->data;
s.push(p);
p=p->left;
}//出循环的时候一条路上的所有偏左的节点都被访问过了
if(!s.empty()){//依次取出路径上保存的元素,从他们的右节点继续上面的循环
p=s.top();
s.pop();
p=p->right;
}//这里如果p->right ==null不会执行while(p)循环,而是再次去取栈顶元素,从下一个右节点开始。
}
}
不用栈(三叉链表):
void preOrder(Node* r){
Node* p =r;//三叉链表的parent节点方便了回溯,因为parent节点反应了从上到下的遍历路径,因此可以通过父节点找到遍历路径上的节点
while(p){
cout<<p->data;
if(p->left){//先使劲往左遍历,边遍历边输出
p=p->left;
}else if(p->right){//如果节点只有右子树,就使劲往右遍历
p=p->right;
}else{//对于叶子节点,需要向上回溯找到第一个未被访问的第一个右子树的根节点
Node* q=p->parent;
while(q && (q->right==p || !q->right)){
//q->right==p表明从左往上回溯,不符合
//q->right == NULL完全没右子树,当然也不符合找右子树根节点的规则
p=q;
q = q->parent;
}
if(!q){//全部访问完的时候 p=r,q=NULL,结束循环
break;
}
}
}
}
后面除了双栈就不写注释了,太麻烦。思想都是一样的。
中序遍历
用栈:
void inOrder(Node* r){
stack<Node*> s;
Node* p = r;
while(!s.empty() || p){
while(p){
s.push(p);
p=p->left;
}
if(!s.empty()){
p=s.top();
s.pop();
cout<<p->data;
p=p->right;
}
}
}
不用栈(三叉链表):
void inOrder(Node* r){
Node* p =r;
Node* q;
while(p){
if(p->left){
p=p->left;
}else if(p->right){
cout<<p->data;
p=p->right;
}else{
cout<<p->data;
Node* q=p->parent;
while(q){
if(!q->right){
cout<<q->data;
}else if(q->left==p){
cout<<q->data;
break;
}
p=q;
q = q->parent;
}
if(!q){
break;
}
}
}
}
后序遍历
用栈:
void inOrder(Node* r){
stack<Node*> s1,s2;
//用两个栈来存储,第一个栈是从右往左的访问顺序,第二个栈的接收顺序是先根再左再右,符合后序遍历规则
Node* p;
s1.push(p);
while(!s1.empty()){
p = s1.top();
s1.pop();
if(p->left){
s1.push(p->left);
}
if(p->right){
s1.push(p->right);
}
//注意这里先左子树入栈s1,再右子树入栈s2,然后根节点入栈s2
//那么在后面的循环里面,必定右子树的节点先入栈s2,左子树的节点后入栈s2
//导致的结果就是,根节点被压在栈底,左子树次之,右子树最上
s2.push(p);
}
while(!s2.empty()){
p=s2.top();
s2.pop();
cout<<p->data;
}
}
不用栈(三叉链表):
void postOrder(Node* r){
Node* p =r;
Node* q;
while(p){
if(p->left){
p=p->left;
}
if(p->right){
p=p->right;
}else{
cout<<p->data;
q=p->parent;
while(q){
if(!q->right){//右子树不存在。就输出它,继续向上找
cout<<q->val<<" ";
p=q;
q=q->parent;
continue;
}
if(q->left==p){//如果是从左边过来的,右子树就是回溯的节点
p=q->right;
break;
}else{//如果是从右边过来的,说明左右子树都已经访问完了,这个节点可以输出了,继续向上回溯
p=q;
q=q->parent;
cout<<p->val<<" ";
}
}
if(!q){//所有元素都输出完的终点是q==NULL,跳出循环
break;
}
}
}
}