数据探索

数据探索

1.数据概况

2.数据离散程度

3.分布形状的探索

4.分布情况探索

5.相关性

6.分类型变量

7.连续变量

数据准备

set.seed(100)
w<-rnorm(1000,0,1)

1. 数据概况

summary(w)

    Min.  1st Qu.   Median     Mean  3rd Qu.     Max.
-3.32078 -0.64970  0.03690  0.01681  0.70959  3.30415 

2.离散程度度量

2.1 方差

总体方差计算公式：

为总体方差，

为变量，

为总体均值，

为总体例数。

var(w)
1.06211

2.2 标准差

公式为

sd(w)
1.06211

2.3 极差

R<-max(w)-min(w)
R
6.624933

半极差 上下四份位数之差

2.4 样本标准误

3.分布形状的探索

3.1 偏度系数

对称性指标，关于均值对称，则系数为0，

右侧更分散，则系数为正，否则为负。

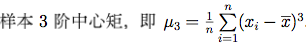
3.2 峰度系数

当数据总体分布为正态分布时，峰度系数近似为0；

当分布较正态分布的尾部更分散时，峰度系数为正；否则为负

当峰度系数为正时，两侧极端数据较多；

当峰度系数为负时，两侧极端数据较少。

data_outline<-function(x){
n<-length(x) #样本个数
m<-mean(x) #样本均值
v<-var(x) #样本方差
s<-sd(x) #样本标准差
me<-median(x) #样本中位数
cv<-100*s/m #样本变异系数
css<-sum((x-m)^2) #样本校正平方和
uss<-sum(x^2) #样本未校正平方和
R<-max(x)-min(x) #样本极差
R1<-quantile(x,3/4)-quantile(x,1/4) #样本半极差
sm<-s/sqrt(n)
g1<-n/((n-1)*(n-2))*sum((x-m)^3)/s^3 #样本峰度系数
g2<-((n*(n+1))/((n-1)*(n-2)*(n-3))*sum((x-m)^4)/s^4-(3*(n-1)^2)/((n-2)*(n-3))) #样本偏度系数
data.frame(N=n,Mean=m,Var=v,std_dev=s,Median=me,std_mean=sm,CV=cv,CSS=css,USS=uss,R=R,R1=R1,Skewness=g1,Kurtosis=g2,row.names=1)}



     N       Mean      Var  　　std_dev     Median     std_mean       CV      　　CSS      USS        R     　　  R1  　Skewness    Kurtosis
  1000 0.01680509 1.062112 1.030588 0.03690212 0.03259005 6132.593 1061.049 1061.332 6.624933 1.359288 -0.0412859 0.03231766

3.3散点图

hist(w,freq=FALSE)
lines(density(w))

 

3.4直方图

plot(w)

3.5 QQ图

qqnorm(w)

 

4.分布情况探索

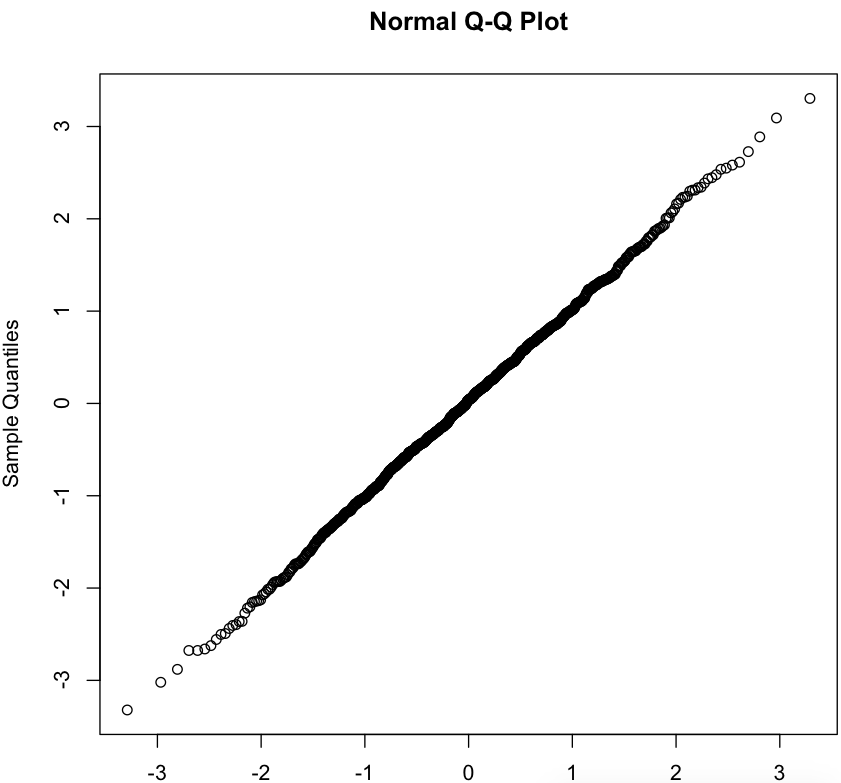
4.1 fitdistrplus包

>require(fitdistrplus)
>descdist(w)
summary statistics
------
min:  -3.320782   max:  3.304151
median:  0.03690212
mean:  0.01680509
estimated sd:  1.030588
estimated skewness:  -0.0412859
estimated kurtosis:  3.032318 

> plot(fitdist(w,"norm"))

5.相关性

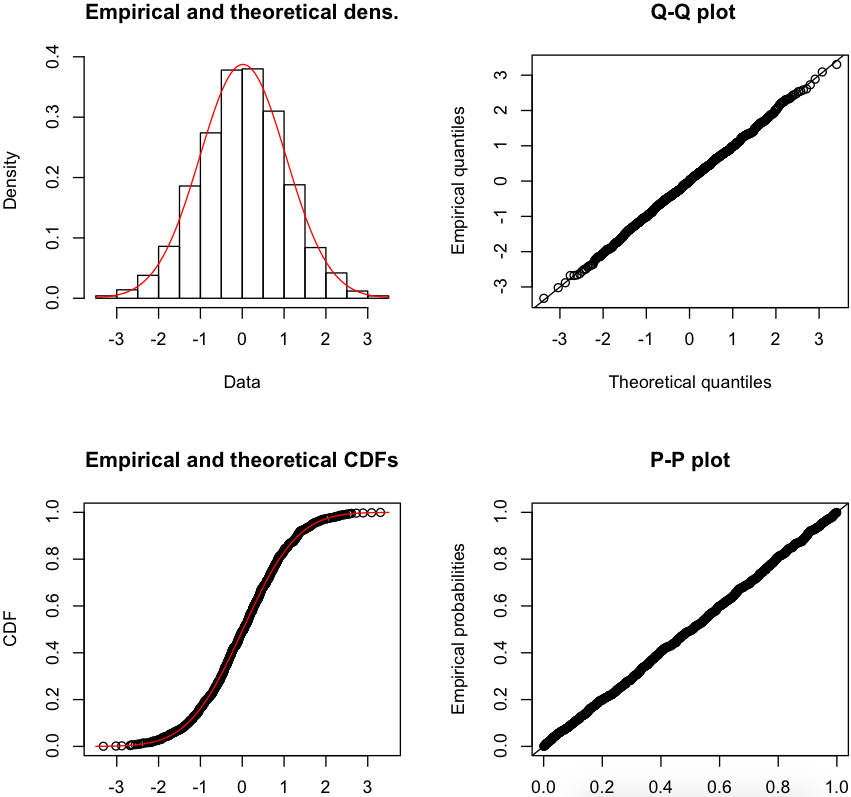
R中能够实现相关性矩阵可视化的程序包

Function	Package	Description
plotcorr	ellipse	以椭圆代表相关系数。
plotcov	pcaPP	用于两个相关系数矩阵的比较。
corrplot	corrplot	相关系数矩阵可视化专业户，推荐。
corrplot	arm	可被ggcorr 完美代替。
ggcorr	GGally	实用性不强。
corrgram	corrgram	比ggcorr 强一点。

6.分类变量分析

Data:Download
train<-read.csv(./train.csv)
attach(train)
table(Sex, Survived)
        Survived
Sex        0   1
  female  81 233
  male   468 109
plot(table(Sex, Survived)

library(dplyr)

summarise(group_by(train,Survived),mean=mean(Fare))
# A tibble: 2 x 2
  Survived     mean
     <int>    <dbl>
1        0 22.11789
2        1 48.39541

summarise(group_by(train,factor(Survived)),meanAge=mean(Age[!is.na(Age)]),meanFare=mean(Fare[!is.na(Fare)]))
# A tibble: 2 x 3
  `factor(Survived)`  meanAge meanFare
              <fctr>    <dbl>    <dbl>
1                  0 30.62618 22.11789
2                  1 28.34369 48.39541

detach(train)

7.连续变量分析

library(car)
scatterplot(SalePrice ~ YearBuilt, data=train,  xlab="Year Built", ylab="Sale Price", grid=FALSE)

scatterplot(SalePrice ~ YrSold, data=train,  xlab="Year Sold", ylab="Sale Price", grid=FALSE)

参考：

1.Wiki QQ

2.Wiki PP

3. R

4.经管之家

回到顶部