经典的动态规划拆点问题。
题目描述
策策同学特别喜欢逛公园。公园可以看成一张 NN 个点 MM 条边构成的有向图,且没有 自环和重边。其中1号点是公园的入口, NN 号点是公园的出口,每条边有一个非负权值, 代表策策经过这条边所要花的时间。
策策每天都会去逛公园,他总是从1号点进去,从 NN 号点出来。
策策喜欢新鲜的事物,它不希望有两天逛公园的路线完全一样,同时策策还是一个 特别热爱学习的好孩子,它不希望每天在逛公园这件事上花费太多的时间。如果1号点 到 NN 号点的最短路长为 dd ,那么策策只会喜欢长度不超过 d + Kd+K 的路线。
策策同学想知道总共有多少条满足条件的路线,你能帮帮它吗?
为避免输出过大,答案对 PP 取模。
如果有无穷多条合法的路线,请输出 -1−1 。
输入输出格式
输入格式:
第一行包含一个整数 TT , 代表数据组数。
接下来 TT 组数据,对于每组数据: 第一行包含四个整数 N,M,K,PN,M,K,P ,每两个整数之间用一个空格隔开。
接下来 MM 行,每行三个整数 a_i,b_i,c_iai,bi,ci ,代表编号为 a_i,b_iai,bi 的点之间有一条权值为 c_ici 的有向边,每两个整数之间用一个空格隔开。
输出格式:
输出文件包含 TT 行,每行一个整数代表答案。
说明
【样例解释1】
对于第一组数据,最短路为 33 。 $1 – 5, 1 – 2 – 4 – 5, 1 – 2 – 3 – 5$ 为 33 条合法路径。
【测试数据与约定】
对于不同的测试点,我们约定各种参数的规模不会超过如下
| 测试点编号 | TT | NN | MM | KK | 是否有0边 |
|---|---|---|---|---|---|
| 1 | 5 | 5 | 10 | 0 | 否 |
| 2 | 5 | 1000 | 2000 | 0 | 否 |
| 3 | 5 | 1000 | 2000 | 50 | 否 |
| 4 | 5 | 1000 | 2000 | 50 | 否 |
| 5 | 5 | 1000 | 2000 | 50 | 否 |
| 6 | 5 | 1000 | 2000 | 50 | 是 |
| 7 | 5 | 100000 | 200000 | 0 | 否 |
| 8 | 3 | 100000 | 200000 | 50 | 否 |
| 9 | 3 | 100000 | 200000 | 50 | 是 |
| 10 | 3 | 100000 | 200000 | 50 | 是 |
对于 100%的数据, 1 le P le 10^9,1 le a_i,b_i le N ,0 le c_i le 10001≤P≤109,1≤ai,bi≤N,0≤ci≤1000 。
数据保证:至少存在一条合法的路线。
题目分析
计数题那么当然首先考虑dp啊。这是一个经典的拆点模型。由于k非常小,所以可以把每一个点拆成$k$个状态。
以上就是拆点的核心。
dp状态怎么设①
“拆点”听上去很高端,但实际上应该大家都在写题时不知不觉应用过。这里可以用$f[i][j]$表示$dis[1][i]=mnDis[1][i]+j$的方案数,其中$mnDis[1][i]$表示1到i的最短路径长度。
之所以$j$这一维代表的路径长度是$mnDis[1][i]+j$,是因为1..i的最短路长度是固定的,可以预先处理,而不用在状态里枚举。(这个和所谓的“dp套dp”非常像,本质就是通过预处理节省时间复杂度)
那么有了状态就很容易想到大概的转移思路了。用$dis[i]$表示1...i的最短路长度,那么通过一条边$(u,v,w)$存在$f[u][d]->f[v][dis[u]+d+w-dis[v]]$。
假设现在已经判断完是否存在零环了(这个对边排序或者怎么搞都行),那么具体的转移方程应该是怎么样的?
dp转移怎么搞①ⅰ
最初我是想:既然$f[u][d]->f[v][dis[u]+d+w-dis[v]]$,并且必定有$dis[u]+w≥dis[v]$,那么每一次转移时$f[i][j]$这个状态的$j$必定是单调增的啊,那么从$f[1][0]$开始对图进行记忆化搜索不就好了吗?
麻烦就麻烦在这样dp转移还受到多条最短路的干扰。

举个最简单的例子,这个做法先$1->4$遍历到了$f[4][0]$一次,然后用这个$f[4][0]=1$向外贡献答案。然而过了一会儿从1开始的路径$1->2->3->4$又遍历到了$f[4][0]$,于是又用$f[4][0]=2$向外贡献答案。这样不就重复计算了吗!
当然可以每次遍历到的时候先减去上一次的贡献再处理。但是这样便既不是我们最初想要达到的,又变得十分冗长,况且并不是没有改进的方法。
dp转移怎么搞①ⅱ ——70pts dp
在没有零边的情况下,注意到dp的顺序一定是先做$dis[]$小的,再做$dis[]$大的。那么就可以以端点到原点距离对于边排序,再做一次稳定的$O(mk)$转移。

1 //由于是按照另一种写法改编而来,所以这份代码有点丑 2 #include<bits/stdc++.h> 3 const int maxn = 100035; 4 const int maxm = 200035; 5 6 int n,m,T,k,p,deal,DIS,mnDis,ans; 7 int initNxt[maxm],initHead[maxn],initEdgeTot; 8 int nxt[maxm],head[maxm],edgeTot; 9 int judge4cir0[maxn]; 10 int dis[maxn][2]; 11 int f[maxn][53]; 12 bool bad[maxn],visQ[maxn]; 13 struct Edge 14 { 15 int u,v,val; 16 long long w; 17 Edge(int b=0, int c=0):v(b),val(c) {} 18 }edgesSv[maxm],initEdges[maxm],edges[maxm]; 19 struct cmp 20 { 21 bool operator()(int a, int b) 22 { 23 return dis[a][DIS] > dis[b][DIS]; 24 } 25 }; 26 std::priority_queue<int, std::vector<int>, cmp> disQ; 27 28 int read() 29 { 30 char ch = getchar(); 31 int num = 0; 32 bool fl = 0; 33 for (; !isdigit(ch); ch = getchar()) 34 if (ch=='-') fl = 1; 35 for (; isdigit(ch); ch = getchar()) 36 num = (num<<1)+(num<<3)+ch-48; 37 if (fl) num = -num; 38 return num; 39 } 40 bool cmpEdge1(Edge b, Edge a) 41 { 42 if (b.val!=a.val) return b.val < a.val; 43 return b.w < a.w; 44 } 45 bool cmpEdge2(Edge a, Edge b) 46 { 47 if (dis[a.u][0]!=dis[b.u][0]) return dis[a.u][0] < dis[b.u][0]; 48 return dis[a.v][0] < dis[b.v][0]; 49 } 50 void initAddedge(int u, int v, int w) 51 { 52 initEdges[++initEdgeTot] = Edge(v, w), initNxt[initEdgeTot] = initHead[u], initHead[u] = initEdgeTot; 53 } 54 void addedge(int u, int v, int w) 55 { 56 edges[++edgeTot] = Edge(v, w), nxt[edgeTot] = head[u], head[u] = edgeTot; 57 } 58 bool legal() 59 { 60 memset(judge4cir0, -1, sizeof judge4cir0); 61 while (edgesSv[deal+1].val==0&&deal<m) 62 { 63 deal++; 64 int u = edgesSv[deal].u, v = edgesSv[deal].v; 65 if (judge4cir0[u]==v) return 0; 66 initAddedge(u, v, 0); 67 judge4cir0[v] = u; 68 } 69 return 1; 70 } 71 void dijsktra(int s) 72 { 73 disQ.push(s), dis[s][DIS] = 0; 74 while (disQ.size()) 75 { 76 int tt = disQ.top(); 77 disQ.pop(), visQ[tt] = 0; 78 for (int i=initHead[tt]; i!=-1; i=initNxt[i]) 79 { 80 int v = initEdges[i].v, w = initEdges[i].val; 81 if (dis[tt][DIS]+w < dis[v][DIS]){ 82 dis[v][DIS] = dis[tt][DIS]+w; 83 if (!visQ[v]){ 84 visQ[v] = 1; 85 disQ.push(v); 86 } 87 } 88 } 89 } 90 } 91 void dp(int x, int y) 92 { 93 printf("f[%d][%d]:%d ",x,y,f[x][y]); 94 for (int i=head[x]; i!=-1; i=nxt[i]) 95 { 96 int v = edges[i].v, w = edges[i].val; 97 printf("f[%d][%d], v:%d, w:%d ",x,y,v,w); 98 if (y+dis[x][0]+w-dis[v][0] > k) continue; 99 (f[v][y+dis[x][0]+w-dis[v][0]] += f[x][y]) %= p; 100 dp(v, y+dis[x][0]+w-dis[v][0]); 101 } 102 } 103 int main() 104 { 105 // freopen("lg3953.in","r",stdin); 106 // freopen("lg3953.out","w",stdout); 107 T = read(); 108 while (T--) 109 { 110 memset(initHead, -1, sizeof initHead); 111 memset(dis, 0x3f3f3f3f, sizeof dis); 112 memset(head, -1, sizeof head); 113 memset(bad, 0, sizeof bad); 114 memset(f, 0, sizeof f); 115 n = read(), m = read(), k = read(), p = read(); 116 ans = mnDis = deal = edgeTot = initEdgeTot = 0; 117 for (int i=1; i<=m; i++) 118 edgesSv[i].u = read(), edgesSv[i].v = read(), 119 edgesSv[i].w = 1ll*edgesSv[i].u*edgesSv[i].v, edgesSv[i].val = read(); 120 std::sort(edgesSv+1, edgesSv+m+1, cmpEdge1); 121 if (!legal()){ 122 puts("-1"); 123 continue; 124 } 125 for (int i=deal+1; i<=m; i++) 126 initAddedge(edgesSv[i].u, edgesSv[i].v, edgesSv[i].val); 127 DIS = 0, dijsktra(1); 128 memset(initHead, -1, sizeof initHead); 129 initEdgeTot = 0; 130 for (int i=1; i<=m; i++) 131 initAddedge(edgesSv[i].v, edgesSv[i].u, edgesSv[i].val); 132 DIS = 1, dijsktra(n); 133 mnDis = dis[n][0], f[1][0] = 1; 134 for (int i=1; i<=n; i++) 135 if (dis[i][0]==dis[0][0]||dis[i][1]==dis[0][0]||dis[i][0]+dis[i][1] > mnDis+k) 136 bad[i] = 1; 137 std::sort(edgesSv+1, edgesSv+m+1, cmpEdge2); 138 for (int d=0; d<=k; d++) 139 for (int i=1; i<=m; i++) 140 { 141 int u = edgesSv[i].u, v = edgesSv[i].v, w = edgesSv[i].val; 142 if (!bad[u]&&!bad[v]) 143 { 144 int tt = d+dis[u][0]+w-dis[v][0]; 145 if (tt <= k){ 146 (f[v][tt] += f[u][d]) %= p; 147 } 148 } 149 } 150 for (int i=0; i<=k; i++) (ans += f[n][i]) %= p; 151 printf("%d ",ans); 152 } 153 return 0; 154 }
dp转移怎么搞①ⅲ ——100pts dp
那么有零边意味着什么呢?意味着仅仅需要对于零边单独拓扑序处理即可。
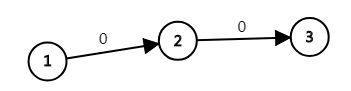
这是一个仅用$dis[]$排序而不够的例子。
dp状态怎么设②
但其实dp题的状态是一个很玄妙的东西。
用$mnDis[i]$表示i到n的最短路,那么这一次$f[i][j]$表示的是$dis[i][n]+j≤mnDis[i]$的方案数。
注意前一种状态是严格=的方案数,而这里利用了前缀和的方法,表示了所有≤的方案数。
dp转移怎么搞②
这样表示的好处在于:从$f[1][k]$直接开始,并不用考虑拓扑序,可以记忆化搜索,并且遇到处理过状态的直接return即可。原因便是这种状态下,答案的贡献是被动的;而不是答案从自身这个状态转移出去。因此一旦搜索到终点$i==n$,$f[i][d]$就可以+1,同时在这个状态路径上的其他所有状态,都会且仅会收到一次这个合法状态的反馈。
或许有点绕口……?不过细想也就是这个理。
还注意到在这种遍历方式之下,如果访问到了尚未出栈的节点,就意味着出现了零环。因此可以省去预判断零环的过程。
那么就可以愉快地记忆化搜索啦。
1 #include<bits/stdc++.h> 2 const int maxn = 100035; 3 const int maxm = 200035; 4 5 int n,m,T,k,p,ans; 6 int nxt[maxm],head[maxm],edgeTot; 7 int dis[maxn]; 8 int f[maxn][53]; 9 bool visQ[maxn],stk[maxn][53]; 10 struct Edge 11 { 12 int u,v,val; 13 Edge(int b=0, int c=0):v(b),val(c) {} 14 }edgesSv[maxm],edges[maxm]; 15 struct cmp 16 { 17 bool operator()(int a, int b) 18 { 19 return dis[a] > dis[b]; 20 } 21 }; 22 std::priority_queue<int, std::vector<int>, cmp> disQ; 23 24 int read() 25 { 26 char ch = getchar(); 27 int num = 0; 28 bool fl = 0; 29 for (; !isdigit(ch); ch = getchar()) 30 if (ch=='-') fl = 1; 31 for (; isdigit(ch); ch = getchar()) 32 num = (num<<1)+(num<<3)+ch-48; 33 if (fl) num = -num; 34 return num; 35 } 36 void addedge(int u, int v, int w) 37 { 38 edges[++edgeTot] = Edge(v, w), nxt[edgeTot] = head[u], head[u] = edgeTot; 39 } 40 void dijsktra(int s) 41 { 42 disQ.push(s), dis[s] = 0; 43 while (disQ.size()) 44 { 45 int tt = disQ.top(); 46 disQ.pop(), visQ[tt] = 0; 47 for (int i=head[tt]; i!=-1; i=nxt[i]) 48 { 49 int v = edges[i].v, w = edges[i].val; 50 if (dis[tt]+w < dis[v]){ 51 dis[v] = dis[tt]+w; 52 if (!visQ[v]) 53 visQ[v] = 1, disQ.push(v); 54 } 55 } 56 } 57 } 58 int dp(int x, int y) 59 { 60 if (f[x][y]) return f[x][y]; 61 if (stk[x][y]) return -1; 62 if (x==n) f[x][y]++; 63 stk[x][y] = 1; 64 for (int i=head[x]; i!=-1; i=nxt[i]) 65 { 66 int v = edges[i].v, w = edges[i].val; 67 int tt = y-dis[v]+dis[x]-w; 68 if (tt>=0){ 69 int tmp = dp(v, tt); 70 if (tmp==-1){ 71 stk[x][y] = 0; 72 return -1; 73 } 74 (f[x][y] += f[v][tt]) %= p; 75 } 76 } 77 stk[x][y] = 0; 78 return f[x][y]; 79 } 80 int main() 81 { 82 // freopen("lg3953.in","r",stdin); 83 T = read(); 84 while (T--) 85 { 86 memset(dis, 0x3f3f3f3f, sizeof dis); 87 memset(head, -1, sizeof head); 88 memset(f, 0, sizeof f); 89 n = read(), m = read(), k = read(), p = read(), edgeTot = 0; 90 for (int i=1; i<=m; i++) 91 edgesSv[i].u = read(), edgesSv[i].v = read(), edgesSv[i].val = read(); 92 memset(head, -1, sizeof head); 93 edgeTot = 0; 94 for (int i=1; i<=m; i++) 95 addedge(edgesSv[i].v, edgesSv[i].u, edgesSv[i].val); 96 dijsktra(n); 97 memset(head, -1, sizeof head); 98 edgeTot = 0; 99 for (int i=1; i<=m; i++) 100 addedge(edgesSv[i].u, edgesSv[i].v, edgesSv[i].val); 101 printf("%d ",dp(1, k)); 102 } 103 return 0; 104 }
推荐相关
题解 P3953 【逛公园】https://kelin.blog.luogu.org/solution-p3953
END
