很典型的按照边考虑贡献的题。
题目描述
小A居住的城市可以认为由n个街区组成。街区从1到n依次标号街区与街区之间由街道相连,每个街区都可以通过若干条街道到达任意一个街区,共有n-1条街道。其中标号为i的街区居住了i名居民。居民会去拜访别人,但是要花费dis(u,v)的过路费,u是他所在的城市,v是他拜访的人所在的城市。你需要求出,所有人都拜访其他人一次花费的过路费之和。
输入格式
第一行一个整数nn接下来n-1行,每行2个整数n−1n−1个整数描述n-1条街道
输出格式
一个整数,表示总花费之和
样例输入
5
1 2
2 3
2 4
1 5
样例输出
184
数据规模与约定
对于30%的数据,满足n≤200n≤200
对于60%的数据,满足n≤3000n≤3000
对于100%的数据,满足n≤1000000n≤1000000
题目分析
是一道典型的按边统计答案的题。但为什么我又没想出来啊。
题目求的是∑u∑v∗dis(u,v),那么来考虑一下问题的瓶颈在哪里。
按照定义直接做
首先是按照定义直接做的想法。
那么统计枚举所有点对,是 O(n^2) 的,预处理 dis(u,v) 有 O(n^3) 的floyd;还有 O(n^2) 的做 n 次dfs。
然而这个方向的做法空间复杂度是肯定要 O(n^2) 的,而且统计枚举的复杂度也难以改进。
考试时候就是吊死在这颗树上没出来了……
分边考虑贡献
统计时候不要那么“直接”,而是把整个答案分部分来考虑。
对于每一个点,与之相关的答案是 i*∑dis[i] 。于是我们发现最后的答案是只与 sum_{dis_i} 有关的。也就是说,对于点 x ,如果预处理了以它为根的 dis[] ,那么其贡献就是可以 O(1) 求出的。因此,解题瓶颈从处理点对的 dis[u][v] 变为了转移 dis[i] 。
对此,Cptraser表示有一种神奇的“平衡移动”方法。
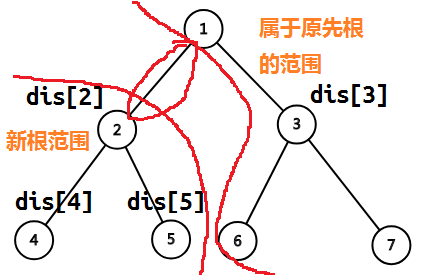
这里(1,2)这条边是正在枚举的边。我们现在要做的是快速将 ∑dis[](以1为根) 转为 ∑dis[](以2为根) 。
图画出来后就很显然了。有$sum_{newDis[]} qquad quad =sum_{dis[]} quad +tot_v-2*size[v]$ 。其中 size[v] 表示以 v 为根子树大小。当然这里所谓的子树大小是要提前人为确定一个根节点的。
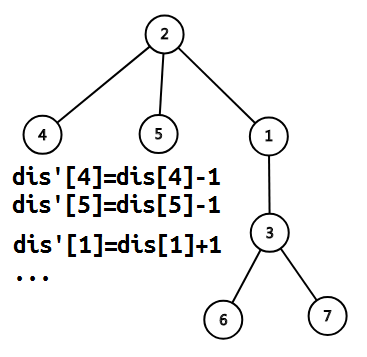
这般把答案分部分之后,我们就会惊喜地发现复杂度降为$O(n+m)$了。
1 #include<bits/stdc++.h> 2 typedef long long ll; 3 const ll MO = 1e9+7; 4 const int maxn = 1000035; 5 const int maxm = 2000035; 6 7 int n; 8 int edges[maxm],nxt[maxm],head[maxn],edgeTot; 9 ll tmp,ans,sum,dis[maxn],size[maxn]; 10 11 int read() 12 { 13 char ch = getchar(); 14 int num = 0; 15 bool fl = 0; 16 for (; !isdigit(ch); ch = getchar()) 17 if (ch=='-') fl = 1; 18 for (; isdigit(ch); ch = getchar()) 19 num = (num<<1)+(num<<3)+ch-48; 20 if (fl) num = -num; 21 return num; 22 } 23 void addedge(int u, int v) 24 { 25 edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot; 26 edges[++edgeTot] = u, nxt[edgeTot] = head[v], head[v] = edgeTot; 27 } 28 void dfs1(int x, int fa) 29 { 30 size[x] = x; 31 for (int i=head[x]; i!=-1; i=nxt[i]) 32 if (edges[i]!=fa) 33 dis[edges[i]] = dis[x]+1, dfs1(edges[i], x), size[x] += size[edges[i]]; 34 } 35 void dfs2(int x, int fa) 36 { 37 ll cnt = 0; 38 for (int i=head[x]; i!=-1; i=nxt[i]) 39 if (edges[i]!=fa){ 40 int v = edges[i]; 41 cnt = (sum-2ll*size[v])%MO; 42 tmp = (tmp+cnt)%MO; 43 ans = (ans+tmp*v%MO)%MO; 44 dfs2(v, x); 45 tmp = (tmp-cnt+MO)%MO; 46 } 47 } 48 ll qmi(ll a, ll b) 49 { 50 ll ret = 1; 51 while (b) 52 { 53 if (b&1) ret = ret*a%MO; 54 a = a*a%MO, b >>= 1; 55 } 56 return ret; 57 } 58 int main() 59 { 60 memset(head, -1, sizeof head); 61 // freopen("city.in","r",stdin); 62 // freopen("city.out","w",stdout); 63 n = read(); 64 for (int i=1; i<n; i++) addedge(read(), read()); 65 dfs1(1, 0); 66 for (int i=2; i<=n; i++) tmp += 1ll*i*dis[i]; 67 ans = tmp, sum = 1ll*(n+1)*n/2; 68 dfs2(1, 0); 69 printf("%lld ",ans*qmi(2, MO-2)%MO); 70 return 0; 71 }
END