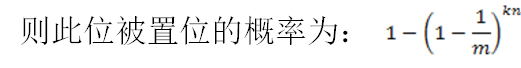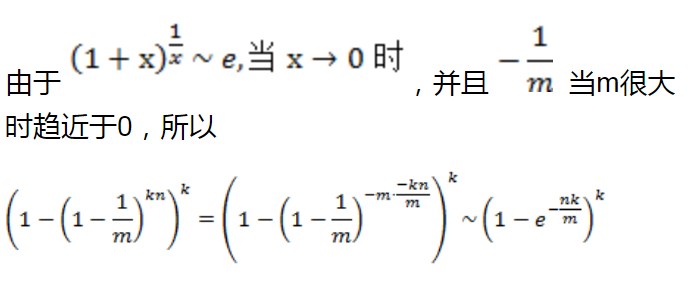简要谈及布隆过滤器
Preface
不负责的出题人扔了一道5e5,2M卡内存的题,标算布隆过滤器,然而std自己用std::set 70M碾过去了。
没学OI时候草草看过这个,不过忘得差不多了。
今天自己考试时候写的假布隆过滤器在$10^5$时候都会有10来个误判(而且这空间怎么卡啊)。
网上的资料大抵都是工程向,这里从OI角度随意谈谈布隆过滤器吧。
所谓“布隆过滤器”?
可以先浅显地理解为 低配版的多哈希 ,因为这东西的最大卖点就是空间复杂度较哈希小得多;但是正确性又不能丢太多,所以就在压缩空间的前提下多用几个哈希函数来增加正确性。
这里有一个卡空间的基础操作:bitset.因为一般的方法bool是8bit只能表示一个数的存在与否;而一个int有32bit,以位可以来表示32个数的存在。
先做说明几个变量的含义:
- $n$:总计插入$n$个元素
- $m$:实现的共有$m$位的bitset.
- $k$:有$k$个不同的hash函数,每个值域在$[0,m)$之间
其实现过程是:对于每次插入,计算得到$k$个哈希值,然后把全局的bitset这$k$个位置修改成1;每次询问,在全局的bitset里查询是否$k$个位置都是1.
没错这个东西感性理解上去就是误判率很高——对OI来说确实了。
下面一段就是课件里关于正确性证明的搬运……
假设布隆过滤器中的hash function满足simple uniform hashing假设:每个元素都等概率地hash到m个slot中的任何一个,与其它元素被hash到哪个slot无关。

(我琢磨着课件好像也是哪里copy来的)
这东西在OI里是不是没什么用
应该是的。
除了丧心病狂+不负责任的出题人会来出道布隆过滤器的题目之外,这玩意(优点:时间换空间;缺点:一定的误判率)在OI里似乎没什么用场。
END