一类带标号图的计数
题目大意
求$n$个点的带标号欧拉图计数;再稍微转换一下得到答案。
题目分析
限于一些原因,本篇博客只介绍带标号欧拉图计数的操作。
前置芝士:图$G$为欧拉图当且仅当$G$为连通图且$forall deg_V为偶数$
第一种方法:组合数学
记$f_i$为$i$个点带标号欧拉图个数;$g_i$为满足$i$个点度数均为偶数的图个数。
对于$g_i$有:$g_i=2^{C ^2_{i-1}}$
意即取出$i-1$个点,对于$C ^2_{i-1}$条边各自可选可不选;最后使用剩下的$1$个点来平衡所有度数为奇数的点。
对于$f_i$有:$f_i= g_i-sumlimits^{i-1}_{j=1}f_jg_{i-j} {{i-1}choose{j-1}}$
后面这个形式是用来避免算重的。如果简单地$f_i= g_i-sumlimits^{i-1}_{j=1}f_jg_{i-j} {ichoose{j}}$,将会算重这种情况:
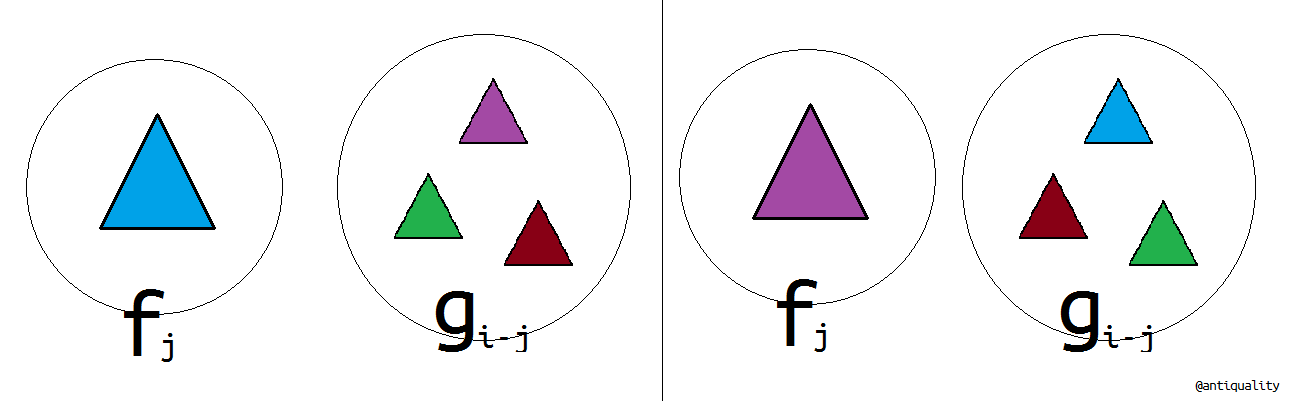
因此,我们可以钦定当前大小为$i$的图的一个特定点一定在$f_j$所处的连通块中,也即$j$就是在枚举特定点所处连通块的大小。
总结一下,对于以上这个式子:$f_jg_{i-j}$表示的是将大小分别为$j$和$i-j$的带标号图合并成大小为$i$的图的方案数量;${i-1}choose{j-1}$表示对于组合出来的图,将其对应到我们所要标号的图上的方案数。
题外话:对于两个相对标号独立的图的合并,我纠结了很久为什么不乘上$ichoose j$(两个具有相对大小的集合合并为更大的具有相对大小的集合的方案数)。后来才意识到如果过早地将两张图对应标号,也就相当于是将特定点的位置移动了。我们之所以要枚举所有$j$来计算${i-1}choose{j-1}$就是为了从这个角度去重。
于是就可以$O(n^2)$递推了。
1 #include<bits/stdc++.h> 2 #define MO 1000000007 3 const int maxn = 2035; 4 5 int n,fac[maxn],facinv[maxn]; 6 int f[maxn],g[maxn]; 7 8 int qmi(int a, int b) 9 { 10 int ret = 1; 11 for (; b; b>>=1, a=1ll*a*a%MO) 12 if (b&1) ret = 1ll*ret*a%MO; 13 return ret; 14 } 15 int C(int n, int m){return 1ll*fac[n]*facinv[m]%MO*facinv[n-m]%MO;} 16 void init() 17 { 18 fac[0] = fac[1] = facinv[0] = facinv[1] = 1; 19 for (int i=2; i<=2000; i++) 20 fac[i] = 1ll*fac[i-1]*i%MO, 21 facinv[i] = MO-1ll*facinv[MO%i]*(MO/i)%MO; 22 for (int i=2; i<=2000; i++) 23 facinv[i] = 1ll*facinv[i]*facinv[i-1]%MO, 24 f[i] = g[i] = qmi(2, ((i-1)*(i-2))>>1); 25 f[1] = g[1] = 1; 26 } 27 int main() 28 { 29 init(), scanf("%d",&n); 30 for (int i=1; i<=n; i++) 31 for (int j=1; j<i; j++) 32 f[i] = ((f[i]-1ll*f[j]*g[i-j]%MO*C(i-1, j-1))%MO+MO)%MO; 33 printf("%d ",1ll*f[n]*C(n, 2)%MO); 34 return 0; 35 }
第二种方法:生成函数