优雅地处理树上的冗余信息
虚树
虚树顾名思义,重点在于建出一颗新的与原树不同的“虚拟”的树。
回顾一下树上的一些问题,会发现时间复杂度常常耗费在大量的无用遍历上面。虚树正是为解决这一问题而产生:通过只保留必要的节点,从而在时间复杂度的阶上达到优化效果。
那么哪些点才是“必要的点”?由于树上问题的核心在于路径,而常见的处理路径的技巧是将树强制为有根树再以根为起点处理每一个点的信息,那么路径$(u,v)$可以划分成$(root,lca),(lca,u),(lca,v)$三个阶段。因而所有询问点的两两LCA就是我们必要的节点。
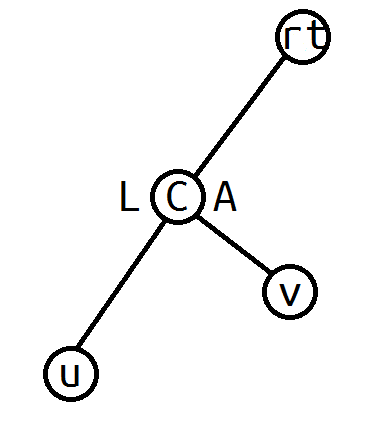
现在既然知道了虚树的构建,那么就该考虑一下实现了。
zzq的介绍写得挺欢快的。
1 void insert(int x) 2 { 3 if (top==1) stk[++top] = x; 4 else{ 5 int lca = Lca(x, stk[top]); 6 while (dfn[stk[top-1]] >= dfn[lca]) 7 addedge(stk[top-1], stk[top]), --top; 8 if (lca!=stk[top]) addedge(lca, stk[top]), stk[top] = lca; 9 stk[++top] = x; 10 } 11 }
虚树技巧
- 建虚树的$ ext{stk}$中最后一个元素就是虚树的根节点
- 每用完一次虚树就需要把所有用到过的点清空。那么一种处理方法是:在最后一次dp之后将访问过的点初始化。
一些例题
2286: [Sdoi2011]消耗战
Description
在一场战争中,战场由n个岛屿和n-1个桥梁组成,保证每两个岛屿间有且仅有一条路径可达。现在,我军已经侦查到敌军的总部在编号为1的岛屿,而且他们已经没有足够多的能源维系战斗,我军胜利在望。已知在其他k个岛屿上有丰富能源,为了防止敌军获取能源,我军的任务是炸毁一些桥梁,使得敌军不能到达任何能源丰富的岛屿。由于不同桥梁的材质和结构不同,所以炸毁不同的桥梁有不同的代价,我军希望在满足目标的同时使得总代价最小。
侦查部门还发现,敌军有一台神秘机器。即使我军切断所有能源之后,他们也可以用那台机器。机器产生的效果不仅仅会修复所有我军炸毁的桥梁,而且会重新随机资源分布(但可以保证的是,资源不会分布到1号岛屿上)。不过侦查部门还发现了这台机器只能够使用m次,所以我们只需要把每次任务完成即可。
Input
第一行一个整数n,代表岛屿数量。
接下来n-1行,每行三个整数u,v,w,代表u号岛屿和v号岛屿由一条代价为c的桥梁直接相连,保证1<=u,v<=n且1<=c<=100000。
第n+1行,一个整数m,代表敌方机器能使用的次数。
接下来m行,每行一个整数ki,代表第i次后,有ki个岛屿资源丰富,接下来k个整数h1,h2,…hk,表示资源丰富岛屿的编号。
Output
输出有m行,分别代表每次任务的最小代价。
HINT
对于100%的数据,2<=n<=250000,m>=1,sigma(ki)<=500000,1<=ki<=n-1
题目分析
虚树的题目其实重在考察树形dp,虚树不过是一个外壳。
这题就是虚树的最基础构造应用。
1 #include<bits/stdc++.h> 2 typedef long long ll; 3 const ll INF = 1ll<<60; 4 const int maxn = 250035; 5 const int maxm = 500035; 6 7 struct Edge 8 { 9 int y,val; 10 Edge (int a=0, int b=0):y(a),val(b) {} 11 }edges[maxm]; 12 ll mx[maxn]; 13 int n,k,a[maxn]; 14 int edgeTot,head[maxn],nxt[maxm],top,stk[maxn]; 15 int dfn[maxn],tim,fat[maxn][20],dep[maxn]; 16 17 int read() 18 { 19 char ch = getchar(); 20 int num = 0, fl = 1; 21 for (; !isdigit(ch); ch=getchar()) 22 if (ch=='-') fl = -1; 23 for (; isdigit(ch); ch=getchar()) 24 num = (num<<1)+(num<<3)+ch-48; 25 return num*fl; 26 } 27 void addedge(int u, int v, int c=0) 28 { 29 edges[++edgeTot] = Edge(v, c), nxt[edgeTot] = head[u], head[u] = edgeTot; 30 edges[++edgeTot] = Edge(u, c), nxt[edgeTot] = head[v], head[v] = edgeTot; 31 } 32 void dfs(int x, int fa, ll c) 33 { 34 dfn[x] = ++tim, dep[x] = dep[fa]+1; 35 fat[x][0] = fa, mx[x] = c; 36 for (int i=head[x]; i!=-1; i=nxt[i]) 37 if (edges[i].y!=fa) 38 dfs(edges[i].y, x, std::min(c, 1ll*edges[i].val)); 39 head[x] = -1; 40 } 41 int Lca(int x, int y) 42 { 43 if (dep[x] < dep[y]) std::swap(x, y); 44 for (int i=17; i>=0; i--) 45 if (dep[fat[x][i]] >= dep[y]) x = fat[x][i]; 46 if (x==y) return x; 47 for (int i=17; i>=0; i--) 48 if (fat[x][i]!=fat[y][i]) 49 x = fat[x][i], y = fat[y][i]; 50 return fat[x][0]; 51 } 52 bool cmp(int x, int y){return dfn[x] < dfn[y];} 53 void insert(int x) 54 { 55 if (top==1) stk[++top] = x; 56 else{ 57 int lca = Lca(x, stk[top]); 58 if (lca==stk[top]) return; 59 while (dfn[stk[top-1]] >= dfn[lca]) 60 addedge(stk[top], stk[top-1]), --top; 61 if (lca!=stk[top]) addedge(lca, stk[top]), stk[top] = lca; 62 stk[++top] = x; 63 } 64 } 65 ll dp(int x, int fa) 66 { 67 ll ret = 0, chk = 0; 68 for (int i=head[x]; i!=-1; i=nxt[i]) 69 { 70 int v = edges[i].y; 71 if (v==fa) continue; 72 chk = 1, ret += dp(v, x); 73 } 74 head[x] = -1; 75 return chk?std::min(ret, mx[x]):mx[x]; 76 } 77 int main() 78 { 79 memset(head, -1, sizeof head); 80 n = read(); 81 for (int i=1; i<n; i++) 82 { 83 int u = read(), v = read(), c = read(); 84 addedge(u, v, c); 85 } 86 dfs(1, 0, INF); 87 for (int j=1; j<=17; j++) 88 for (int i=1; i<=n; i++) 89 fat[i][j] = fat[fat[i][j-1]][j-1]; 90 for (int T=read(); T; --T) 91 { 92 edgeTot = 0, top = 1, stk[top] = 1, k = read(); 93 for (int i=1; i<=k; i++) a[i] = read(); 94 std::sort(a+1, a+k+1, cmp); 95 for (int i=1; i<=k; i++) insert(a[i]); 96 for (int i=1; i<top; i++) addedge(stk[i], stk[i+1]); 97 printf("%lld ",dp(1, 1)); 98 } 99 return 0; 100 }