我这种maintain写法好zz。考试时获得了40pts的RE好成绩
In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation
DZY loves Fibonacci numbers very much. Today DZY gives you an array consisting of n integers: a1, a2, ..., an. Moreover, there are mqueries, each query has one of the two types:
- Format of the query "1 l r". In reply to the query, you need to add Fi - l + 1 to each element ai, where l ≤ i ≤ r.
- Format of the query "2 l r". In reply to the query you should output the value of
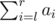modulo 1000000009 (109 + 9).
Help DZY reply to all the queries.
Input
The first line of the input contains two integers n and m (1 ≤ n, m ≤ 300000). The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) — initial array a.
Then, m lines follow. A single line describes a single query in the format given in the statement. It is guaranteed that for each query inequality 1 ≤ l ≤ r ≤ n holds.
Output
For each query of the second type, print the value of the sum on a single line.
题目分析
注意到形如Fib的数列$a_{n+2}=a_{n+1}+a_n$有相当好的性质。
- $a_n=F_{n−2}a_1+F_{n−1}a_2$
- $sum_{i=1}^na_i=a_{n+2}−a_2$
第一条可以用数学归纳法证明；第二条就是将$2sum_{i=1}^na_i$展开，得到$sum_{i=1}^na_i+a_{n+2}-a_2$.
回到这一道题上，利用了这两条性质，那么对于每一个修改的区间只需要保留区间前两项增加的Fib值就可以记录下这个操作。所以现在就可以用线段树来维护这一系列询问了。
1 #include<bits/stdc++.h> 2 #define MO 1000000009 3 typedef long long ll; 4 const int maxn = 300035; 5 6 struct node 7 { 8 ll tag1,tag2,sum; 9 }f[maxn<<3]; 10 int n,m; 11 ll sum[maxn],fib[maxn]; 12 13 int read() 14 { 15 char ch = getchar(); 16 int num = 0, fl = 1; 17 for (; !isdigit(ch); ch=getchar()) 18 if (ch=='-') fl = -1; 19 for (; isdigit(ch); ch=getchar()) 20 num = (num<<1)+(num<<3)+ch-48; 21 return num*fl; 22 } 23 void maintain(int rt, int lens) 24 { 25 f[rt].tag1 %= MO, f[rt].tag2 %= MO; 26 f[rt].sum = f[rt<<1].sum+f[rt<<1|1].sum; 27 f[rt].sum = (f[rt].sum+f[rt].tag1*fib[lens]+f[rt].tag2*fib[lens+1]-f[rt].tag2)%MO; 28 } 29 void pushdown(int rt, int l, int r) 30 { 31 if (!f[rt].tag1&&!f[rt].tag2) return; 32 int mid = (l+r)>>1, ls = rt<<1, rs = rt<<1|1; 33 f[ls].tag1 += f[rt].tag1, f[ls].tag2 += f[rt].tag2; 34 f[rs].tag1 += f[rt].tag1*fib[mid-l]+f[rt].tag2*fib[mid-l+1]; 35 f[rs].tag2 += f[rt].tag1*fib[mid-l+1]+f[rt].tag2*fib[mid-l+2]; 36 f[rt].tag1 = f[rt].tag2 = 0; 37 maintain(ls, mid-l+1); 38 maintain(rs, r-mid); 39 } 40 void modify(int rt, int L, int R, int l, int r) 41 { 42 if (L <= l&&r <= R){ 43 f[rt].tag1 += fib[l-L+1]; 44 f[rt].tag2 += fib[l-L+2]; 45 maintain(rt, r-l+1); 46 return; 47 } 48 int mid = (l+r)>>1; 49 pushdown(rt, l, r); 50 if (L <= mid) modify(rt<<1, L, R, l, mid); 51 if (R > mid) modify(rt<<1|1, L, R, mid+1, r); 52 maintain(rt, r-l+1); 53 } 54 ll query(int rt, int L, int R, int l, int r) 55 { 56 if (L <= l&&r <= R) return f[rt].sum; 57 pushdown(rt, l, r); 58 int mid = (l+r)>>1; 59 ll ret = 0; 60 if (L <= mid) ret += query(rt<<1, L, R, l, mid); 61 if (R > mid) ret += query(rt<<1|1, L, R, mid+1, r); 62 return ret%MO; 63 } 64 int main() 65 { 66 n = read(), m = read(), fib[1] = fib[2] = 1; 67 for (int i=1; i<=n; i++) sum[i] = (sum[i-1]+read())%MO; 68 for (int i=3; i<=300005; i++) fib[i] = (fib[i-1]+fib[i-2])%MO; 69 for (int i=1; i<=m; i++) 70 { 71 int opt = read(), l = read(), r = read(); 72 if (opt==1) modify(1, l, r, 1, n); 73 else printf("%lld ",(query(1, l, r, 1, n)+(sum[r]-sum[l-1])%MO+MO)%MO); 74 } 75 return 0; 76 }
END