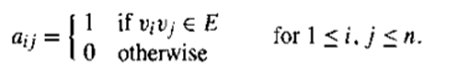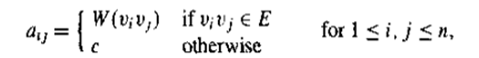7.1简介
许多问题可以转化为一类图的问题，这些问题的起源不仅仅在与计算机相连接，而且在整个自然，工业和商业领域。解决许多图问题的高效算法的发展对人们在所有这些领域解决实际问题的能力有重要的影响。然而，现在许多重要的图问题还没有已知的高效解决方案。对于其他的，还不知道现在已知的解决方案是不是尽可能高效，或者还可以修正以达到进一步的改善。
在本章中，我们介绍图的定义和图的基本属性。然后我们将讲述图的高效遍历的所有的主要的方法。事实证明，许多自然问题都可以高效地迎刃而解-----在线性时间内，事实上------通过使用作为基础的图形遍历.不够严格地说，我们可能称这些“简单的”图问题，不能在这个意义上，很容易找到解决方案或者很容易编程，但是在另一个意义上说，一旦编程，该问题的实例可以高效的解决，它是可行的解决非常大的问题实例(在某些情况下，有百万节点的图)。
继续我们的松散分类，"中间值”图问题这一类是由那些可以在多项式时间内解决的问题组成的。但是比一个基础的图遍历需要做更多的工作。也就是说，对每个“中间值”问题，算法是以上述一些固定的多项式时间为限解决“规模”为n的实例。例如
d为某个其他固定的d。在这个类里许多重要的问题将在第8,9,14章讲解。就今天的强大的计算机上解决相当大量的问题的实例非常实用。
增大规模，就有了没有已知多项式时间算法的“困难的”图问题，在一些情况下，有50到100个节点的图问题不能用已知的任何算法解决，即使运行一年。然而，我们现在的知识不允许我们排除以后发现某个高效算法的可能性。这些问题的真正代表我们的知识前沿，并且他们的甄选将在第13章讨论。
图问题迷人的一面是以一种方式很微小的改变一个被规定的问题就会被放置到三类(简单的，中等的，困难的)中的任何一个，因此熟悉现存的已知问题，并且什么特性致使它们分为简单，中等或者困难的三类，对处理一个新问题很有帮助。
7.2 定义和表示法
非正式的，一个图就是就是点(顶点，或者节点)的有限集合，它们中的一些被线或者带箭头的(边)连接起来。如果边是没有方向的或者“两条路径的”，该图就称为无方向图，如果边是有方向的或者“一条路径的”，该图就称为有方向的图。“有方向的图”有时简称为有向图，“无方向的图”有时简称为无向图。因为人们经常指有方向的和无方向的图都简单地称之为图，这是有歧义的。在可能引起混乱的上下文中，我们将使用具体的术语。一般讨论的图是都指有向图和无向图。
7.2.1 一些例子
图是运筹学，计算机科学，电气工程，经济，数学，物理学，化学，通信，博弈论还有其他许多领域中的许多问题和结构的有用的抽象。思考下列例子：
例7.1 航空公司的航线图
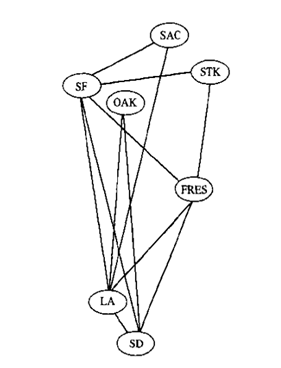
航空公司的航线图可以用无向图来表示。点代表城市，当且仅当两个城市之间在两个方向上都没有停留时，用一条线连接它们。见图7.1是California几座城市之间的航空公司的虚拟航线图。
例7.2 流程图
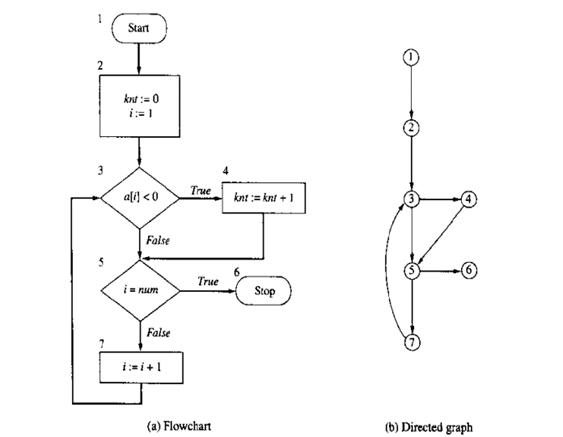
流程图代表了在程序中的控制流、数据流或者在一个过程中的材料，点是流程图方块，连接的箭头是流程的方向。图7.2在Pascal语法中的例子
图7.2流程图和相应的有向图:箭头指示的是流的方向
例7.3 一个二元关系
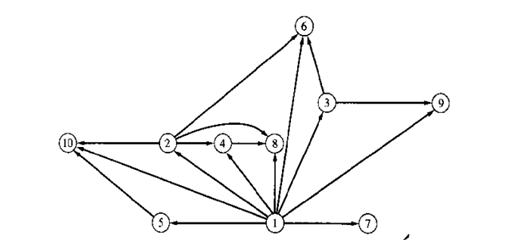
在1.3.1节我们定义了二元关系。定义R是集合S={1,……，10}上的二元关系，S由有序对(x,y)组成，其中X是Y的适当因素；也就是说X≠y，并且y/x余数为0.回想一下，xRy是
一个替代符号。在图7.3的有向图中，点是S中的元素，并且当且仅xRy时从x到y之间会有一个箭头。注意：R具有传递性，如果xRy并且yRz都成立，则xRz也成立。
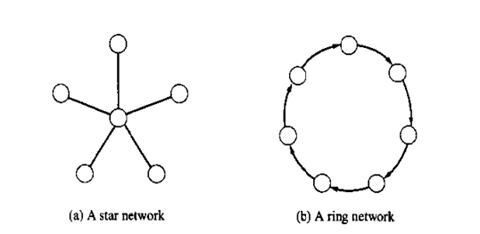
例7.4 计算机网络
点是计算机，线(对于无向图)或者箭头(对于有向图)是通信链路。图7.4是每个的示例。
例7.5 一个电路图
点可以是二极管，晶体管，电容，开关等。如果它们之间有导线连接它们，那么两点之间用线连接。
前面的五个例子对描述有向图和无向图提供的各种不同对象的关系的自然抽象很充分了，包括物理对象和它们的布局例如由航空公司的航线连接的城市，高速公路，铁路，和抽象的物体，例如二元关系和程序的控制结构。这个例子还应该建议一些代表的问题，我们不妨询问的对象和它们之间的关系，将改写在图形方面的问题。这些问题可以用通过在图上的算法来回答。例如，问题“San Diego 和Sacramento之间有没有一个不间断的航班？”将被翻译成“在图7.1中，顶点SD 和SAC之间有没有一条边”，思考下面问题：
1，从San Diego 飞到Sacramento最便宜的路线是什么？
2，那条航线涉及到最少的飞行时间？
3，如果一个城市的机场因为天气不好而关闭，你是否仍然可以在其他各个城市之间飞？
4，如果网络中一台电脑关闭，在网络中的其他各个电脑之间信息是否会呗送达？
5，有多少流量可以从一个指定的点到另一个使用某些指定的道路？
6，一个给定的二元关系是否具有传递性？
7，一个给定的流程图是否有循环？
8，导线应该怎样连接各种各样的电子插座，才能用最少的导线将它们连接到一起？
在本章中和后面，我们将学习算法去回答这些问题。
7.2.2 基本的图的定义
本节关注图的定义和有关图的一般特征。许多声明和定义同时适用于无向图和有向图，并且我们将使用一个共同的符号，以尽量减少重复。然而，某些定义在无向和有向图之间是不同，这些不同将被强调。
定义7.1 有向图
一个有方向图的，或者有向图，是成对的G=(V,E),V是一个集合，该集合的元素被称为顶点，E是一个V中元素的有序对的集合，顶点被称为节点，E中的元素称为边，或者有向边，或者弧。对于E中的有向边(v,w),v是它的尾，w是它的头；(v,w)在图中代表箭头v→w，在下文中，我们简单的写成vw。
在二元关系的例子中(例7.3，图7.3)
V={1,2，……,10}
E={(1,2),…,(1,10),(2,4),(2,6),(2,8),(2,10),(3,6),(3,9)，(4,8),(5,10)}.
定义7.2 无向图
一个无向图是成对的G=(V,E),V是一个集合，该集合的元素称为顶点，E是一个集合，该集合是一组V中不同元素的无序对。顶点经常也被称为节点，E中的元素被称为边，或者无向边，为了强调。每个边都可能被作为V的一个子集，V中包含两个元素，结果是，{v,w}表示一个无向边。在图表中，这个边是线v-w。在下文中，我们简单的写成vw。当然，对于无向图而言，vw=wv。
对于例7.1的图和图7.1，例如，我们有
无向图的定义意味着连接一个顶点到它自己：一条边作为一个包含了两个元素的集合来定义，并且该集合不能有重复的元素，定义(1.3.1节) 。
定义7.3 子图，对称图，完全图
图G=(V,E)的一个子图是图
并且有
和 
，通过关于图的定义，还需要有 
．
对称图是有向图，这样每个边vw也可以翻转为边wv.通过将每个无向边解释为在相反方向上的一对有向边,则每个无向图都有一个相应的对称有向图.
一个完全图是一个(正规的无向的)每两个顶点之间都有一条边的图。
边vw也可以说是顶点v和w之间的事件，反之亦然。
定义7.4 邻接关系
一个图或者有向图G=(V,E)的边包括一个称为邻接关系的关系，A，在顶点的集合上。设v和w是V的元素。那么vAw(读作w邻接于v)当且仅当vw在E中。换句话说，vAw意味着沿着G的一条边，从v可以到达w。如果G是无向的，那么关系A是对称的(也就是，当且仅当vAw，则有wAv)。
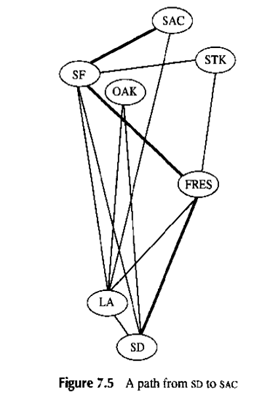
路径的概念在许多应用中是很重要的，包括一些涉及人的路由选择，电话讯息(电子讯息)，汽车交通，管道中的液体或者气体，等等,其他路径代表抽象属性.再思考图7.1并假设我们希望通过飞机从洛杉矶到弗雷斯诺旅行。边{LA,FRES}是一种可能的路由选择，但是还有其他的，我们可以从LA出发到SAC再到SF再到FRES，或者我们可以从LA出发到SD再到FRES。这是从LA到FRES的所有路径。
定义7.5图中的路径
在图G=(V,E)中从v到w的一条路径是边的一组序列
并有
该路径的长度是k。顶点v可以将从v到其自身的路径长度看做0.一条简单的路径
是独立的。
如果从v到w有一条路径，则说顶点w是可达的。
路径{SD,FRES},{FRES,SF},{SF,SAC}见图7.5，我们用呗通过的一列顶点来表示路径。(但是记住路径的长度是遍历的边数)。因此，图7.5的路径是SD,FRES,SF,SAC长度是3.
定义7.6 连通，强连通
连通性的定义需要小心，因为在有向图和无向图中，该定义是不同的。
当且仅当在无向图中，每对顶点v和w，都有从v到w的路径，就说该无向图连通。
当且仅当在有向图中，每对顶点v和w，都有一条路径从v到w，则称有向图是强连通
显然读取是相同的，则单独定义的原因是，在一个无向图中，如果有一条路径从v到w，那么自然而然就有一条路径从w到v。在有向图中，这个不一定为真，因此限定词“强”用来表明，条件较强。如果我们将无向图想象成双向的街道系统，并把有向图想象成单向街道系统，那么强连通性的条件意味着我们通过在它们正确的方向上遍历单向街道，使得我可以从任何一个地方到达任何一个地方，如果他们都是双行道，这显然是一个更严格的条件。
定义7.7 图中的环
定义环需要注意，因为有向图和无向图中的定义不同。
对于有向图，一个环仅仅是一个非空的路径，第一个和最后一个顶点是同一个，并且一个简单的环指没有顶点重复，除了第一个和最后一个是同一个之外。
对于无向图，该定义类似，但是要增加一个要求，如果任意边出现了不止一次，那么它将总是出现在相同的方向上。也就是说，用到定义7.5的表示法，如果
并且 
(0≤i<y),那么久不可能存在j使得 
， 
如果一个图没有环，则称该图是无环的。
一个无环无向图被称为一个无向森林。如果该图式连通的，则称为自由树，或者无向树。
一个无环有向图经常被简称为DAG。
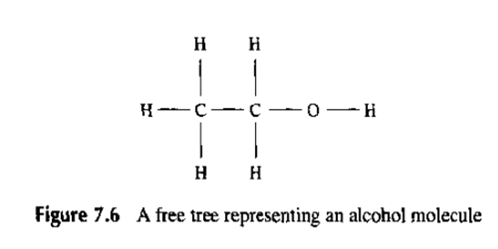
图7.6是一个自由树或者无向图的例子，注意，由于该定义没有顶点是被孤立出来的根。一棵有根树是指一棵树的一个顶点被指定为根。一旦根节点被指定，用于该树的父节点和孩子节点的关系就可以得出。
分别定义一个对称有向图区分无向图的的原因涉及到环。如果环的概念不重要，那么用于有向图的程序通常可用于对称有向图，该有向图对应于一个无向图。然而，如果环在该问题中恰好重要，这个替换就不会起作用。例如，简单的无向图有边ab没有环，但是它的对称副本有两个方向的边ab和ba，并且有环。
定义7.8 连接组件
一个无向图G的连接组件是G的一个极大的连接子图。对于有向图，相应的概念更复杂。它的定义推迟到定义7.18.
我们应该阐明在“连接组件”的定义里面“极大的”的意义，如果在任何一个图的一些收集中它不是一个适当的子图，那么该图被称为在图的一些集合中极大。它不需要最多的顶点也不需要最多的边。在定义7.8中，“集合”是G的所有连接子图。
当术语“组件”用于图的连接和其他抽象结构，它经常带有组中极大的暗示。在后面的章节里我们将遇到术语“强连通组件”和“双连通组件”。在两种情况下，都是极大的概念。
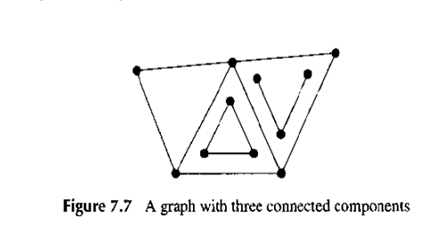
如果无向图没有连接，它可能分割成独立的的连接组件，并且这种分割是唯一的。图7.7中的图有三个连通组件。
在图的许多应用中，很自然涉及到一个数字，通常称之为每条边的权值。这个数字带便代价或者通过一种方式使用特定的一条边来获得利益。思考图7.1，假设我们想从SD飞到SAC。中间没有中转，但是仍然会有几条路由或者路径可以用。哪条是最好的呢？为了回答这个问题，我们需要一个标准来判断各种路径。一些可能的标准：
1，停站的数目
2，总的票价花费
3，总的飞行时间
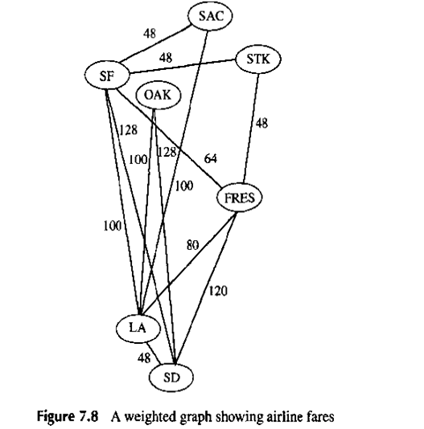
选择一个标准之后，我们可以给图中的每条边分配一个沿着边旅行的成本(停站，时间，金钱)。某条路径的总成本是该路径遍历的边的总的成本。见图7.8，带有写在每条边旁边的飞机票价的航线图。你可以确认从SD到SAC中间停留一战LA最便宜的路径。找出“最好”的路径的问题将在第8.3和9.4节研究。
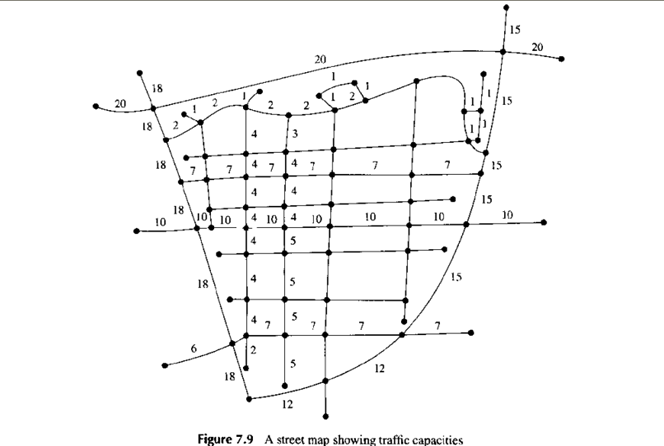
图7.9 显示的是城市的一些街道，可用来研究交通流量。分配给每条边的数字表示在某个时间间隔内，可以通过该街道的交通总量。该数字取决于道路的类型和大小，限制的速度，在图中作为顶点显示的十字路口的交通灯的数量和其他各种因素。
边上的数字的分配发生在应用程序通常足以值得的定义。
定义７.９
一个有权值的图是一个三重关系(V,E,W)，其中(V,E)是一个图(有向或者无向)，W是一个从E到实数R的函数(其他类型的权值，例如有理数，整数，对某个问题适合的)。例如边e，W(e)称为e的权值。
功能术语看起来很专业，但是很容易理解，我们回顾一下在1.3.1节在概念上，一个函数就是一个有两列的表格：函数的参数和对应的函数值。在这种情况下，每条边出现在某行的第一列，它的权值在某行的第二列。这种数据结构的表示法可能不同，但是它携带的信息是一样的。在图的关系图中，我们简单地紧邻每条边写下权值，就像图7.8和7.9中一样。权值在某个应用中将对应的成本或者是一条边不受欢迎的方面，然而在其他问题中权值是容量或者边的其他一些有利的属性(该术语随着应用变化：因此术语成本，长度或者能力都可以由权值代替)。在许多应用中，权值很自然地不能为负，因为当它们代表距离的时候，某个算法的正确性依赖于限制权值不能为负值，当然其他一些算法可以处理负值。
7.2.3图的表示法和数据结构
我们已经知道两种方法在纸上来表示图：通过画顶点由点代替，边由直线或者箭头来代替的图。和通过列举顶点和边。本节讨论的数据结构对在程序中表示图很有用。设G=(V,E)是一个图，其中
并且有V=
.
邻接矩阵表示法
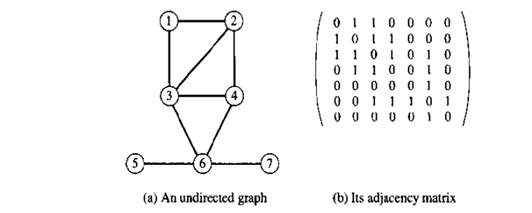
G可以用一个n×n的矩阵
表示，称为G的邻接矩阵，A通过下面定义
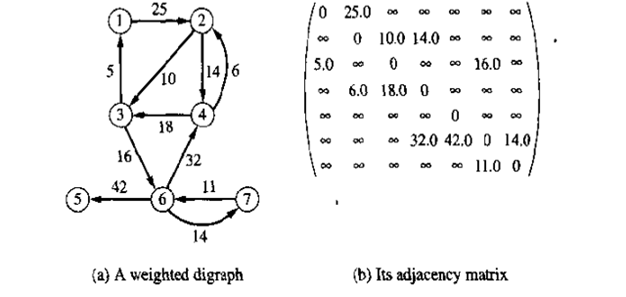
无向图的邻接矩阵式对称的(只有一半需要存储)。如果G=(V,E,W)是一个有权值的图，那么可以通过修改如下定义，利用邻接矩阵存储权值
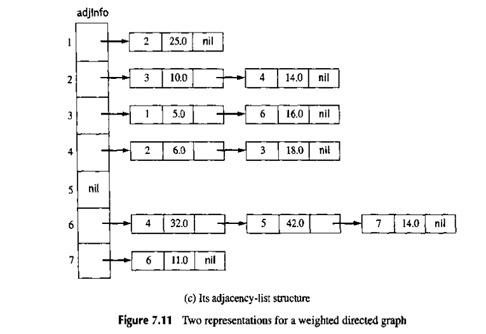
c是一个常数，它的值依赖于对权值的解释和问题的解决。如果权值是成本，则∞会呗选来做c，因为遍历一个不存在边的成本是很高很高的。如果权值是指能力，选择c为0就是很合适的，因为没有东科可以顺着不存在的边移动。见图7.10(a,b)和7.11(a,b)的例子。
依靠图解决某个问题的算法需要检查每条边并至少以某种方式处理一次。如果一个邻接矩阵表示法已经使用，我们不妨认为对不同顶点之间的边的一个图。因为许多算法将检查矩阵中的每个输入来决定哪条边是真正存在的。因为在有向图中可能的边的数目是
，或者在无向图中是n(n-1)/2，该算法的复杂度为
邻接表表示的数组
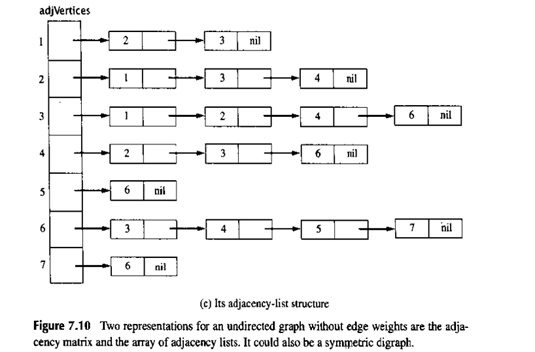
对邻接矩阵的替代是一个通过包含链表的顶点的号码索引的数组，称为邻接表。对于每个顶点
，数组的第i个条目包含的一列信息是G中的所有“离开”的边。在有向图中，这就意味着是一条边的尾部。