参考文章:
判断链表是否相交:http://treemanfm.iteye.com/blog/2044196
一、单链表反转
链表节点

public class Node { private int record; private Node nextNode; public Node(int record) { super(); this.record = record; } }
构建链表

public static Node creatLinkedList() { Node head = new Node(0); Node tmp = null; Node cur = null; for (int i = 1; i < 10; i++) { tmp = new Node(i); if (1 == i) { head.setNextNode(tmp); } else { cur.setNextNode(tmp); } cur = tmp; } return head; }
递归实现

public static Node reverse(Node head) { if (null == head || null == head.getNextNode()) { return head; } Node reversedHead = reverse(head.getNextNode()); head.getNextNode().setNextNode(head); head.setNextNode(null); return reversedHead; }
循环实现

public static Node reverseCircle(Node head){ Node pre=head; Node cur=head.getNextNode(); Node temp; while(cur!=null){ temp=cur.getNextNode(); cur.setNextNode(pre); pre=cur; cur=temp; print(pre); } head.setNextNode(null); return pre; }
二、判断单向链表是否有环
单链表有环有两种形式,整个链表是一个圆环 或者部分成环 如图1:
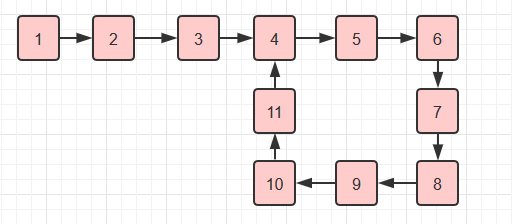
图1
分析:
判断链表是否带环,我们可以采用在头结点设两个指针,一个叫fast,一个叫slow,fast一下走两步,而slow一下走一步。如果链表中存在环的话,那么fast和slow必定会在环中相遇。若链表中没有环的话,那么fast必定现于slow指针先到达链表的尾节点。时间复杂度为O(n),空间复杂度为O(1)
实现:
构建上图有环链表:

public static Node creatLinkedListCircle() { Node head = new Node(1); Node node4 = null; Node tmp = null; Node cur = null; for (int i = 2; i < 13; i++) { tmp = new Node(i); if (2 == i) { head.setNextNode(tmp); } else if(i==4){ cur.setNextNode(tmp); node4=tmp; }else { if(i==12){ cur.setNextNode(node4); }else{ cur.setNextNode(tmp); } } cur = tmp; } return head; }
判断是否有环:

public static boolean isCircle(Node head) { //只有一个节点 if(head.getNextNode()==null){ return false; } //两个结点成环 if(head.getNextNode()==head){ return true; } Node slow = head.getNextNode(); Node fast = head.getNextNode().getNextNode(); while (slow != null && fast != null) { if (slow == fast) { return true; } slow=slow.getNextNode(); fast = fast.getNextNode().getNextNode(); } return false; }
三、判断单向链表是否相交

方案一:
若两个链表都无环且交于一点,那么最后一个节点一定是共有的。可以先遍历第一个链表,记录最后一个节点,再遍历第二个链表,将其最后一个节点与第一个链表的最后一个节点比较,若相同,则相交。时间复杂度也为O(Max(length(h1),length(h2))),空间复杂度为O(1)
方案二:
①循环遍历h1,计算每个节点的hash值并存入map中;
②循环遍历h2,顺序计算每个节点的hash值v,并用map.get(v),若返回非空,则算法结束
第①步算法时间复杂度O(length(h1)),第②步算法时间复杂度O(length(h2)),因此hash计数 算法时间复杂度为O(max(length(h1),length(h2))),复杂度降低到线性。但是由于使用了额外的map结构,空间复杂度为O(length(h1))。
方案三:
求出两个链表的长度:len_h1,len_h2,求出差值len(len为较大的减去较小的值)。让长的那个先走len步,之后两个链表一起走,直至节点相同的时候。时间复杂度为O(Max(length(h1),length(h2))),空间复杂度为O(1)
方案三:
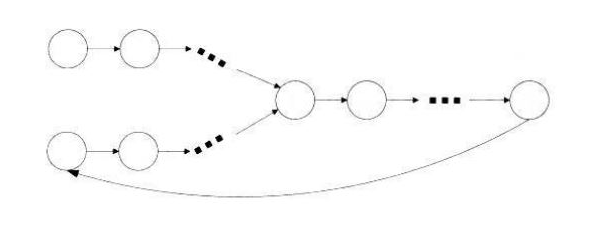
如果两个链表都无环,则可以把第二个链表接在第一个链表后面,如果得到的链表有环,则说明这两个链表相交。这里如果有环,则第二个链表的表头一定在环上,只需要从第二个链表开始遍历,看是否会回到起点即可判断。假设两个链表长度分别为m和n,则时间复杂度为O(m+n)。
三、求环的长度
分析:
我们可以采用在头结点设两个指针,一个叫fast,一个叫slow,fast一下走两步,而slow一下走一步。slow和fast从第一次相遇到第二次相遇时所走的长度即是环的长度.参考图1
实现:

public static int getCircleLength(Node head) { Node slow = head.getNextNode(); Node fast = head.getNextNode().getNextNode(); int length=0; boolean flag=false; while (slow != null && fast != null) { if (slow == fast) { if(flag){ return length; } length=0; flag=true; } length++; slow=slow.getNextNode(); fast = fast.getNextNode().getNextNode(); } return length; }
四、求环入口点
方案一:采用hash的方式。遍历该链表,第一个重复的node则为环入口点。时间复杂度O(n),空间复杂度O(n)

public static Node getEnterNode(Node head) { Map<Node, String> map = new HashMap<Node, String>(); map.put(head, null); Node next = head.getNextNode(); // 找到交点 while (next != null) { if (map.containsKey(next)) { return next; } map.put(next, null); next = next.getNextNode(); } return null; }
方案二:经过推导,头结点到 入口点的距离 和 问题二的交点 到入口点的距离是相等的。所以可以设置分别从两点设置指针。第一次相遇的节点 则为环入口点。时间复杂度O(n),空间复杂度O(1)

public static Node getEnterNode(Node head) { Node slow = head.getNextNode(); Node fast = head.getNextNode().getNextNode(); //找到交点 while (slow != null && fast != null) { if (slow == fast) { break; } slow = slow.getNextNode(); fast = fast.getNextNode().getNextNode(); } //分别从头结点和交点出发,第一次相遇 则为环入口点 Node no = head.getNextNode(); slow = slow.getNextNode(); while (slow != no) { no = no.getNextNode(); slow = slow.getNextNode(); } return no; }
五、查找单链表的中间节点
分析:采用快慢指针的方法。设两个指针,一个叫fast,一个叫slow,fast一下走两步,而slow一下走一步。fast走完时,slow恰好走到中间。

public static Node getMidNode(Node head) { Node slow = head; Node fast = head; while (fast!=null&&fast.getNextNode()!=null) { slow=slow.getNextNode(); fast=fast.getNextNode().getNextNode(); } return slow; }
六、求链表倒数第k个节点
分析:设置两个指针 p1、p2,首先 p1 和 p2 都指向 head,然后 p2 向前走 k 步,这样 p1 和 p2 之间就间隔 k 个节点,最后 p1 和 p2 同时向前移动,直至 p2 走到链表末尾。
实现:

//查找倒数第k个节点 public static Node getLastKNode(Node head,int k) { Node p1 = head; Node p2 = head; while (k-->0) { p2=p2.getNextNode(); } while(p2!=null){ p2=p2.getNextNode(); p1=p1.getNextNode(); } return p1; }
七、合并两个有序链表,并保持有序

// 合并两个有序链表 public static Node merge(Node head1, Node head2) { if (head1 == null) { return head2; } if (head2 == null) { return head1; } Node head = null; if (head1.getRecord() < head2.getRecord()) { head = head1; head.setNextNode(merge(head1.getNextNode(), head2)); } else { head = head2; head.setNextNode(merge(head1, head2.getNextNode())); } return head; }
