WC2022 Solution Set

我喜欢 $ 题，哕哕哕。

只找一天一节课听。

（OJ 找题比赛搜索 WC2022）

Day 1 直觉与证明

我直觉证明了个锤。

题太多不想补了。

CF1267G Game Relics

有一个可能太简单导致不好发现的结论，当前状态如果选择了随机抽，那么会随机抽直到抽到一个。

根据这天讲的 canonicalize（决策规范化），我们考虑将两个操作分开执行（可以用同样出处的 exchange argument 证明，交替执行的策略不会更优）。那么在先执行随机抽和先买中显然先随机抽更优秀（毕竟一开始抽中的概率会大一些，这是个直观的东西）。

然后是，我们要找到一个时间点，使得在之前我们选择随机抽，在之后直接买。定义 \(f_i\) 为选择了 \(i\) 个东西之后，再买一个随机的东西的期望花费。抽中没抽到的东西的概率是 \(\dfrac{n-i}{n}\)，那么期望抽 \(\dfrac{n}{n-i}\) 次。那么 \(f_i = \dfrac{x}{2}\left( \dfrac{n}{n-i} -1 \right) + x\)。

注意到随机抽去买这个动作得到的东西我根本不知道，也无法操控。将随机抽归纳到直接买是不可行的。

Motivation: 将直接买这个操作，通过先随机抽再直接买这个性质，变成跟随机抽一个性质。

记没买的东西的总价值为 \(c\)，还有 \(p\) 个没选。注意到在两个操作都是通过固定花费随机购买一个东西，那么每种购买顺序概率相同，当前如果直接买相当于期望花费 \(\dfrac{c}{p}\) 买一个随机的还没有的东西。

那么在确定了 \(c,p\) 的情况下，我们的最优决策固定，花费为 \(\min\left(f_{n-p},\dfrac{c}{p}\right)\)。

观察数据范围，猜测需要 \(O(n^2 \sum c_i)\) 的算法。因此我们可以求出选了 \(p\) 个东西总价格为 \(c\) 的方案数。

因为每种购买顺序概率已经相同了，可以求出 \(dp_{p,c}\) 表示选了 \(p\) 个东西总价格为 \(c\) 的概率，相当于方案数再除以 \(\dbinom{n}{p}\)。

那么最优的答案是 \(\displaystyle \sum_{i=0}^{n-1} C(i)\)，其中 \(C(i)\) 表示在选择了 \(i\) 个东西之后再选择一个东西的最优期望花费。

显然 \(C(i)\) 也是个求和的形式。令 \(s = \sum c_i\)，枚举剩下的东西的总价格 \(c\)，那么 \(\displaystyle C(i) = \sum dp_{i,c} \cdot \min\left(f_i,\dfrac{s-c}{n-i}\right)\)。

Submission.

CF1510I Is It Rated?

Motivation: 每次猜测之后会给答案，我们每次尽量跟着猜对多的人猜。

准确来说，猜对越多的人，他的权威就越大，正确的可能就越大；当然如果出现只有他一个人猜 \(1\) 其他人猜 \(0\) 的情况我们会选 \(0\)，这是因为每个人有一定权重。

只给出一种方法去猜，能过就行。毕竟是直觉题。

Submission.

Day 2 $ 题

原来是 $ 题！！！

IOI2021 Registers

\(s=0\) 的情况。对于 \(n\) 个数，我们比较 \((1,n/2+1),(2,n/2+2),\cdots\) 并将其赋值到 \(1,2,\cdots\) 上。这样就可以将 \(n\) 缩小一半，操作次数是 \(O(w \log n)\)（\(w\) 是缩小一半的操作次数）。

考虑如何比较两个数的大小（这种造计算机题要么不给比大小要么不给加法，生气）。若 \(a<b\)，则 \(a-b<0\)，此时注意到 \(a,b\) 是无符号整数。如果 \(a-b<0\)，其符号位一定为 \(1\)。考虑用符号位判断。

注意到我们封装了加法，需要实现减法。那么 \(a-b = a+(\operatorname{not} b + 1)\)。再加一个常量求符号位，微调可以做到这一点。

然后是排序。注意到的是，一般的常用算法快排或者归并需要知道哪个位置是什么数，依赖之前的结果。显然我们的寄存器操作不支持做到这一点。那么考虑一些并行的排序算法，比如奇偶排序，这样做到的是奇数位和偶数位比较，需要完成相邻每个数的比较与交换，这个类似于上面的过程，只是 \(n=2\) 并且位置不同罢了。

还可以使用双调排序。

Submission.

UOJ671 诡异操作

哕题。把除法中 \(v=1\) 的操作除去，每个数最多被除 \(O(\log a_i)\) 次，因此维护过程中我们需要考虑把除法这个操作看成对一个固定区间重构，考虑线段树。

然后是，这个除法要重构，一个好的想法是叶子存储的信息里面直接保存下来一个当前位置的值就好了。

显然对每一个 bit 考虑。共有 \(128\) 个 bit 位。一个结点中存下这 \(128\) 个 bit 位在这个区间里出现的次数 \(d_0,d_1,\cdots ,d_{127}\)。

注意到，假设这个区间长度为 \(l\)，那么将所有 \(d\) 二进制展开，长度为 \(O(\log l)\)。这是一个 \(128 \times \log l\)（表示列乘行）的表。讨厌的是我们的区间长度可能并不是 \(2^k\) 的形式，我们将 \(n\) 补至 \(2^k\) 即可。

但是这样还是很烦……注意到我们之前做的是把行缩成一个值，不如这次把列缩成一个值。这样变成一个 \(1 \times \log l\) 的表，每个数都是 \(128\) 位的数。与操作支持打标记，对于一个结点的直接修改可以直接将表与上修改值。查询类似于二进制加法，直接算。

时间复杂度 \(O(n \log a_i+q\log^2 n)\)。

Submission.

UOJ592 新年的聚会

有一个我不知道怎么证的结论是，一个有 \(m\) 条边的图，可以划分成 \(O(\sqrt m)\) 个独立集。

那就直接分了……$ 哥哥告诉我们 \(5\times 10^4 ≈ O(m \log n), 10^6 ≈ O(n \sqrt m)\)。拿出 \(O(\sqrt m)\) 似乎也是合理的。

那么，求独立集是个很简单的事情。我们维护每个独立集，看一下这个点能否加进去某一个，不行就再加一个就好了。

然后是处理独立集与独立集之间的边。两个独立集 \(S,T\) 之间如果有边，假设 \(|S|\geq |T|\)，将 \(S\) 尽量均匀划分成两块，如果有边相连就向下递归直到 \(|S|=|T|=1\) 即可。

Submission.

UOJ604 赶路

显然有解。求出凸包，分类讨论。但是我不会凸包，怎么办啊！！1

考虑分治。有函数 \(\operatorname{Solve}(s,t,S)\) 表示找到一个路径 \(s \to t\) 并经过且只经过 \(S\) 里面的所有点。这个随便搞，将 \(S\) 分成两部分 \(P,Q\)，递归走 \(\operatorname{Solve}(s,S_0,P)\) 和 \(\operatorname{Solve}(S_0,t,Q)\)。

其实是我不会复杂度证明哈哈hhhhhhh。

Submission.

CF566C Logistical Questions

需要证明一个结论是，答案类似于凸函数，大概是说以答案的结点为根的树，父亲的答案总不劣于儿子的答案。

有想法是，随机一些边，找到两个点计算答案。把不优的那一边删掉，但是还是不能保证复杂度。

那么保证不优的那一边至少是当前树大小的一半就好了。不难想到重心，选一个优秀的，用类似点分治的过程。

但是不妙的是我们不可能对每一个子结点都算一遍答案。考虑求导，找导数小于 \(0\) 的那一边走过去就好了。

Submission.

Day 3 邓题

节目效果非常好，感谢 ccf，感谢邓老师。

AGC044E Random Pawn

luogu 刚好到这场 AGC 就不爬了，生气。

显然如果到了 \(a_i\) 最大的位置就不会再走，破环成链，重复一遍最大值。

注意到每个 \(f_i\) 都有 \(f_i = \max\left(a_i,\dfrac{(f_{i-1}+f_{i+1})}{2}-b_i\right)\) 这样的表达，想到 USACO Balance Beam 一题，只不过带了个 \(b_i\) 这种恶心东西。

考虑将 \(a_i\) 减去 \(b_i\)，然后对每个 \(f_i\) 加上一个系数 \(c_i\)，就可以消去 \(\max\) 表达式里面的 \(c_i\)。

\(c_i\) 的求法是，钦定 \(c_1=0\)，剩下的是一堆可解的方程。不想多讲。

那么 \(f_i = \max\left(a'_i,\dfrac{(f_{i-1}+f_{i+1})}{2}\right)\)。画出 \((i,f_i)\) 的所有点。

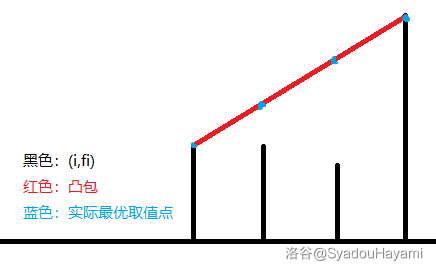
不言而喻一目了然，在凸包点上再动减少的期望肯定大于增加的期望，不动更好，因此在凸包点上一定会停止。求出凸包算多个梯形面积就好了。注意有 \(c_i\) 系数的存在。

Submission.

Od deski do deski

就是那个砍树从世界上消失那个题。

注意到 \(n\) 棵树最多用 \(n\) 个颜色……所以定义可以转成 \(n\) 二维相关。

定义 \(f_{i,j},g_{i,j}\) 分别表示前 \(i\) 个用了 \(j\) 个颜色，并且方案合法或不合法的方案。合法的方案只可能加入之前出现过的颜色并且一定可行，不合法的方案分情况讨论是加入新颜色还是不加入，转移。答案也很显然。

Code.

stars

先考虑如何 \(O(n k!)\) 判断一个子段是否奇妙。枚举 \(0 \sim k-1\) 的排列 \(p\)，\(p_i\) 表示现在已经用了 \(i\) 个坐标，若当前星星加不进去我们就把这个星星的 \(p_i\) 维加上，使得其能被加上去。

如果能把所有星星加完就合法。

那么，定义 \(dp_{i,p}\)（一个长度为 \(k\) 的数组）表示从 \(i\) 开始，用 \(p\) 这个排列去匹配，\(dp_{i,p,j}\) 表示 \(p_j\) 维第一次失配的位置。

从后往前走，每次在前面加上一个数。分类讨论。

如果 \(dp_{i+1,p}\) 中的 \(p_0\) 维，\(i\) 和 \(i+1\) 相同，我们可以直接转移；

否则，转移到的 \(dp_{i,p,0}\) 一定是 \(i+1\)。我们要找到一个合法的情况转移过来。假设是从 \(dp_{i+1,q}\) 转移过来，只需要在里面找到第一个 \(a_i\) 失配，并且 \(p_0\) 维相同的位置即可。

比较抽象，推荐看代码。

算了我还是具体讲一下。我们想把 \(q\) 分成三部分，记作 \(A,p_0,B\)（其中 \(p_0\) 是单独做的一部分）。转移到的 \(p\) 形式上就是 \(p_0AB\)。注意到 \(A\) 可以管控 \(i+1 \sim [p_0]-1\)（其中 \([p_0]\) 表示 \(p_0\) 一维在 \(q\) 中加入的位置），并且在 \([p_0]\) 和 \(i\) 时我们都需要 \(p_0\) 的话，我们可以把 \(p_0\) 提前变成 \(p\)。这样可以找到一个合法的 \(q\)。找法也说明得很清楚了，显然 \(a_{i,p_0} = a_{[p_0],p_0}\)。

找不到的话只有令 \(q=Ap_0B\) 了。

Code.

CFgym 103470L Secret of Tianqiu Valley（南京的构造）

一个灯只有按和不按两种可能。确定第一盏和第二盏按不按就可以知道后面的按不按。处理 \(n=3\) 的情况可以扩展到所有的情况，讨论了做下就好啦。

Submission.

LOJ3519 Flop Sorting

注意到这个操作可逆，这个问题就变成对一个序列排序。

枚举排序算法，考虑归并排序。

我们的操作支持反转有序数列，那么考虑归并，按照值域分治反转。放个 x义x 的图（侵删）。

不言而喻，一目了然。

Submission.

PA2021 Round 2A Poborcy podatkowi

定义 \(dp_{i,0/1/2/3}\) 表示 \(i\) 子树中以 \(i\) 为根，挂了一条长度为 \(i\) 的链的最大选择方案的权值。

然后是，\(1\) 和 \(3\) 匹配，\(2\) 和 \(2\) 匹配，\(0\) 基本可以不管。枚举子树状态（挂了多长的链）。

这样的话我们在做类似背包的过程中只需要管 \(2\) 的奇偶性和 \(1,3\) 的数量差绝对值。

但是 \(1,3\) 数量差可能巨大……怎么办？邓告诉我们只需要 shuffle 一次就能做到随机啦！不知道为什么。

一个结点向下只能挂一条链。考虑一下哪些状态合法需要保存就好了。

Code.

Snackdown 2021 Final Robbery

有一些可能是构造被用烂了的方法是，套入这个题，\(2p\) 个物品可以分成大小为 \(p\) 的两组，质量和不超过 \(n\)。

定义 \(f(k,w)\) 表示答案。按下面的方式递归：

• 如果 \(k\) 是奇数，我们先随便选一个 \(i\)，那么进入 \(f(k-1,w-i)\)，得到 \(a_i\) 的收益，进入下一层；
• 否则，我们将其分成两组，它们的质量差为 \(2d \in [-n,n]\)，进入 \(f(k/2,w-d)+f(k/2,w+d)\)，继续递归。

不同的 \(k\) 是 \(O(\log k)\) 级别的。反正是大力记忆化。

Code.

Snackdown 2021 Final Queue at the Bakery

定义 \(dp_{i,j,k}\) 表示还要接待 \(i\) 个人，当前服务员还要工作 \(j\) 天，前面有 \(k\) 个服务员优先接客时，被这一服务员接待的客人的等待时间之和。

因为比较状态很暴力转移式不写。但是空间显然是不够的，\(j\) 这一维可能会很大。因为 \(p\in [0.4,0.6]\)，那么 \(d\) 小了 \(j\) 不会很大，\(d\) 大了 \(j\) 在更大的地方的变化是等差数列。反正最后找一个阈值 \(T\)，使得 \(j\) 在此之后都是等差数列了，就可以以一种玄学的优化方式过掉这个题。

重点在阈值的设计。

Code.

AGC056E Cheese

我确实没有听懂邓老师讲的 \(O(n^4)\)……还是搞个 \(O(n^5)\) 的吧。

好题。这个 \(n\) 很小似乎支持我们做很高次方的算法，我们先破环成链计算最后一只老鼠（从 \(0\) 开始编号，这只就是 \(n-1\)）吃不到的概率。

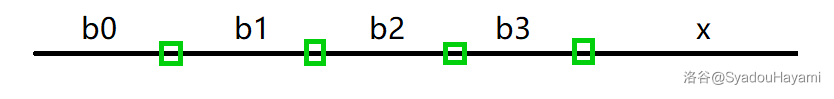
如上定义，绿色表示老鼠 \(0,1,\)。其中 \(b_i\) 是放到这一段的数量，\(x\) 是经过该段的东西的次数。

钦定老鼠 \(n-1\) 吃不到。记 \(c_i\) 为经过老鼠 \(i\) 的东西的次数，不难知道 \(c_i = b_i +x-i\)（放到这一段的一定可以，加上转了一圈的，前面的已经吃了 \(i\) 个）。

那么老鼠 \(n-1\) 吃不到的概率就是，在 \(x\) 个东西经过时老鼠 \(n-1\) 都不吃，并且其他老鼠都吃了的概率。写出来就是：

\[p=2^{-x} \prod_{i=0}^{n-2}\left( 1-2^{-c_i} \right) \]

那么我们枚举 \(x\) 以及 \(b\)，答案就是：

\[\sum_b \sum_x 2^{-x} \prod_{i=0}^{n-2}\left( 1-2^{-c_i} \right) (n-1)! \prod_{i=0}^{n-1} \dfrac{a_i^{b_i}}{b_i!} \]

后面那一坨是分配 \(b\) 的方案数。

枚举 \(b\) 的过程可以采用 dp，但是概率那坨东西确实不好算……

记 \(2^{-x} = z\)。把 \(c_i\) 里面的 \(2^{-x}\) 提出来，这是很多个跟 \(z\) 有关的多项式的乘积。这样就又可以 dp 做了。

对每个都做一遍上述算法即可。

Submission.

Day 4 瑇题

没听呢。不写了。