在pc端设置商家的配送范围,用户在下单时,根据用户设置的配送地点判断是否在可配送范围内,并给用户相应的提示。
下面说下我的实现思路:
1.用百度地图在PC端设置配送范围,可拖拽选择
2.根据用户设置的配送地址判断是否在配送范围内
一、百度地图PC端获取范围
改动百度地图官网的demo,设置配送范围。
思路:获取多边形的顶点,以json的形式保存到数据库。
百度API关于多边形覆盖物:
构造函数:
Polygon(points:Array[, opts:PolygonOptions]) 创建多边形覆盖物
方法:
setPath(path:Array) none 设置多边型的点数组(自1.2新增)
getPath() Array 返回多边型的点数组(自1.2新增)
实现:
//设置配送范围
function setRange(_point, _ppoints) {
var polygon = new BMap.Polygon(_ppoints, {
strokeColor: "blue",
strokeWeight: 2,
strokeOpacity: 0.5
}); //创建多边形
map.addOverlay(polygon); //增加多边形
polygon.enableEditing(); //允许编辑
polygon.addEventListener("lineupdate",
function(e) {
var rangeArr = polygon.getPath();
$("#distributeRange").val(JSON.stringify(rangeArr));
});
}
以上代码主要是监听 lineupdate 事件,每一次拖拽百度地图回调函数将返回的多边形的顶点,然后通过JSON.stringify方法转为string类型存在一个标签里面,以待后续的表单提交操作。
二、判断点是否在范围内
去网上看了一下,判断点是否在配送范围内的方法很多,大概采用的是射线法。
但是有一些方法没有考虑全面,导致有的情况判断不够准确。
在百度地图的GeoUtils里面找到了“判断点是否多边形内”这个方法。
因为我是需要在后端做判断,然后直接把js转化成了java,测试百发百中,欣喜!(后面附上测试方法)
/**
* 判断点是否在多边形内
* @param point 检测点
* @param pts 多边形的顶点
* @return 点在多边形内返回true,否则返回false
*/
public static boolean IsPtInPoly(Point2D.Double point, List < Point2D.Double > pts) {
int N = pts.size();
boolean boundOrVertex = true; //如果点位于多边形的顶点或边上,也算做点在多边形内,直接返回true
int intersectCount = 0; //cross points count of x
double precision = 2e-10; //浮点类型计算时候与0比较时候的容差
Point2D.Double p1,
p2; //neighbour bound vertices
Point2D.Double p = point; //当前点
p1 = pts.get(0); //left vertex
for (int i = 1; i <= N; ++i) { //check all rays
if (p.equals(p1)) {
return boundOrVertex; //p is an vertex
}
p2 = pts.get(i % N); //right vertex
if (p.x < Math.min(p1.x, p2.x) || p.x > Math.max(p1.x, p2.x)) { //ray is outside of our interests
p1 = p2;
continue; //next ray left point
}
if (p.x > Math.min(p1.x, p2.x) && p.x < Math.max(p1.x, p2.x)) { //ray is crossing over by the algorithm (common part of)
if (p.y <= Math.max(p1.y, p2.y)) { //x is before of ray
if (p1.x == p2.x && p.y >= Math.min(p1.y, p2.y)) { //overlies on a horizontal ray
return boundOrVertex;
}
if (p1.y == p2.y) { //ray is vertical
if (p1.y == p.y) { //overlies on a vertical ray
return boundOrVertex;
} else { //before ray
++intersectCount;
}
} else { //cross point on the left side
double xinters = (p.x - p1.x) * (p2.y - p1.y) / (p2.x - p1.x) + p1.y; //cross point of y
if (Math.abs(p.y - xinters) < precision) { //overlies on a ray
return boundOrVertex;
}
if (p.y < xinters) { //before ray
++intersectCount;
}
}
}
} else { //special case when ray is crossing through the vertex
if (p.x == p2.x && p.y <= p2.y) { //p crossing over p2
Point2D.Double p3 = pts.get((i + 1) % N); //next vertex
if (p.x >= Math.min(p1.x, p3.x) && p.x <= Math.max(p1.x, p3.x)) { //p.x lies between p1.x & p3.x
++intersectCount;
} else {
intersectCount += 2;
}
}
}
p1 = p2; //next ray left point
}
if (intersectCount % 2 == 0) { //偶数在多边形外
return false;
} else { //奇数在多边形内
return true;
}
}
主要是判断和这个方法的可行性。
为此写了个测试方法。
思路:获取一个多边形的顶点,然后随机点一个点
1.调用百度地图的方法,判断该点是否在范围内
2.根据百度地图获取的那个店的经纬度,自己程序判断是否在范围内
调用百度地图的方法:
<html>
<head>
<meta content="text/html; charset=utf-8" http-equiv="Content-Type"/>
<title>GeoUtils示例</title>
<script src="http://api.map.baidu.com/api?v=1.2" type="text/javascript"></script>
<script src="http://api.map.baidu.com/library/GeoUtils/1.2/src/GeoUtils_min.js" type="text/javascript"></script>
<style type="text/css">
table {
font-size: 14px;
}
</style>
</head>
<body>
<div id="container" style="float:left;600px;height:500px;border:1px solid gray">
</div>
<div id="control" style="float:left;300px;height:500px;border:1px solid gray">
<table style="100%;">
<tr>
<td colspan="2">
判断点是否在多边形内:
</td>
</tr>
<tr>
<td>
<input onclick="polygon1()" type="button" value="多边形1"/>
</td>
</tr>
<tr>
<td>
<input onclick="polygon2()" type="button" value="多边形2"/>
</td>
</tr>
<tr>
<td>
经度<input id="lng" type="text" value="">
</td>
</tr>
<tr>
<td>
纬度<input id="lat" type="text" value="">
</td>
</tr>
<tr>
<td>
结果:
</td>
</tr>
<tr>
<td>
<p id="result" style="color:red">
</p>
</td>
</tr>
<table>
</div>
</body>
</html>
<script type="text/javascript">
var map = new BMap.Map('container')
var pt = new BMap.Point(116.404, 39.915)
var mkr = new BMap.Marker(pt)
var ply //多边形
map.centerAndZoom(pt, 16)
map.enableScrollWheelZoom() //开启滚动缩放
map.enableContinuousZoom() //开启缩放平滑
//初始化为多边形1
polygon1()
//生成多边形1
function polygon1 () {
var pts = []
var pt1 = new BMap.Point(116.395, 39.910)
var pt2 = new BMap.Point(116.394, 39.914)
var pt3 = new BMap.Point(116.403, 39.920)
var pt4 = new BMap.Point(116.402, 39.914)
var pt5 = new BMap.Point(116.410, 39.913)
pts.push(pt1)
pts.push(pt2)
pts.push(pt3)
pts.push(pt4)
pts.push(pt5)
ply = new BMap.Polygon(pts)
//演示:将面添加到地图上
map.clearOverlays()
map.addOverlay(ply)
}
//生成多边形2
function polygon2 () {
var pts = []
var pt1 = new BMap.Point(116.395, 39.910)
var pt2 = new BMap.Point(116.394, 39.914)
var pt3 = new BMap.Point(116.396, 39.919)
var pt4 = new BMap.Point(116.406, 39.920)
var pt5 = new BMap.Point(116.410, 39.913)
pts.push(pt1)
pts.push(pt2)
pts.push(pt3)
pts.push(pt4)
pts.push(pt5)
ply = new BMap.Polygon(pts)
//演示:将多边形添加到地图上
map.clearOverlays()
map.addOverlay(ply)
}
map.addEventListener('click', function (e) {
mkr.setPosition(e.point)
map.addOverlay(mkr)
//将点击的点的坐标显示在页面上
document.getElementById('lng').value = e.point.lng
document.getElementById('lat').value = e.point.lat
InOrOutPolygon(e.point.lng, e.point.lat)
})
function InOrOutPolygon (lng, lat) {
var pt = new BMap.Point(lng, lat)
var result = BMapLib.GeoUtils.isPointInPolygon(pt, ply)
if (result == true) {
document.getElementById('result').innerHTML = '点在多边形内'
} else {
document.getElementById('result').innerHTML = '点在多边形外'
}
}
</script>
界面如下:
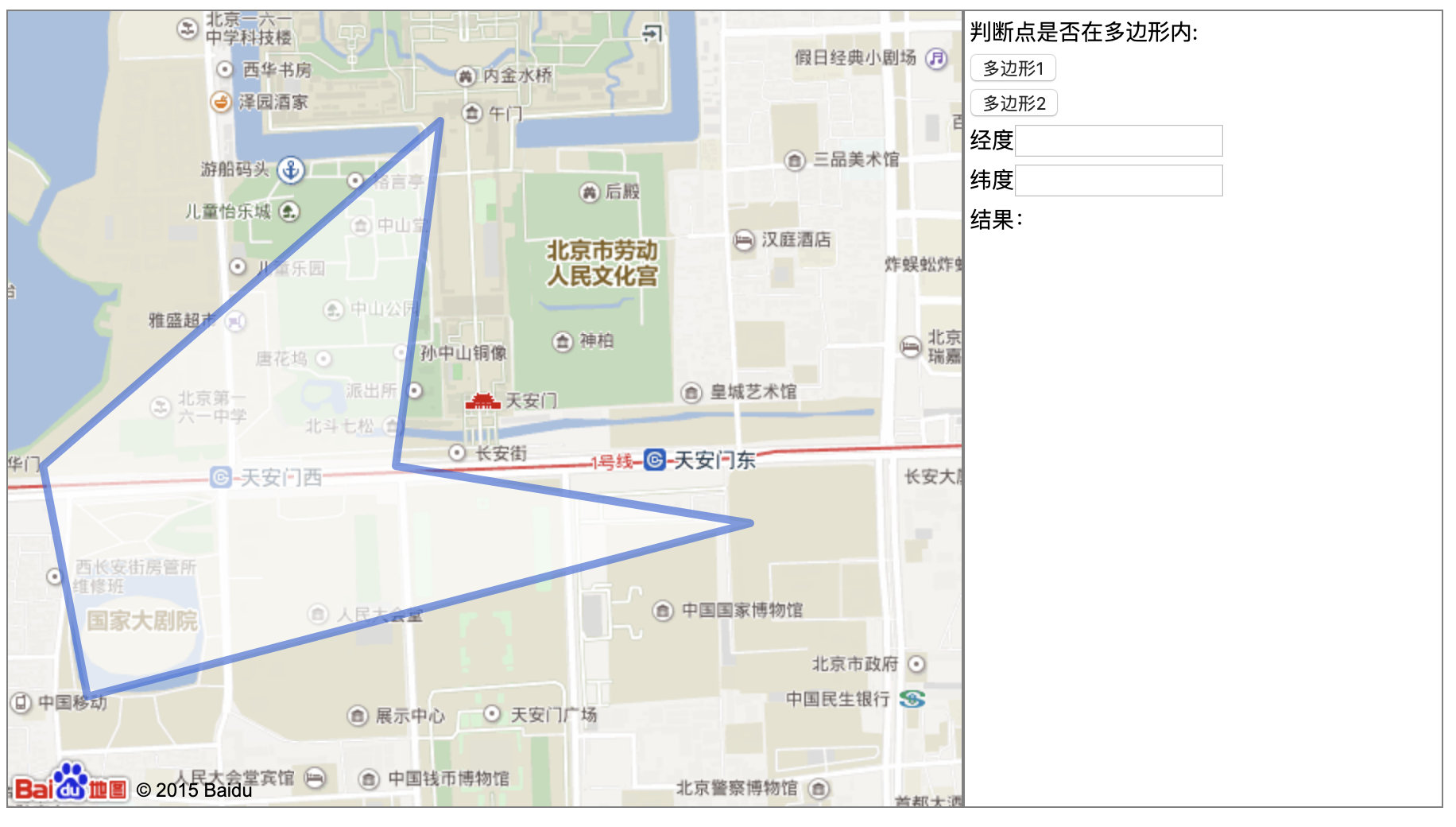
在页面上点击一个点后,获取了该点的坐标(用于自己的方法测试),并调用了 InOrOutPolygon 来判断了该店是否在此范围内。
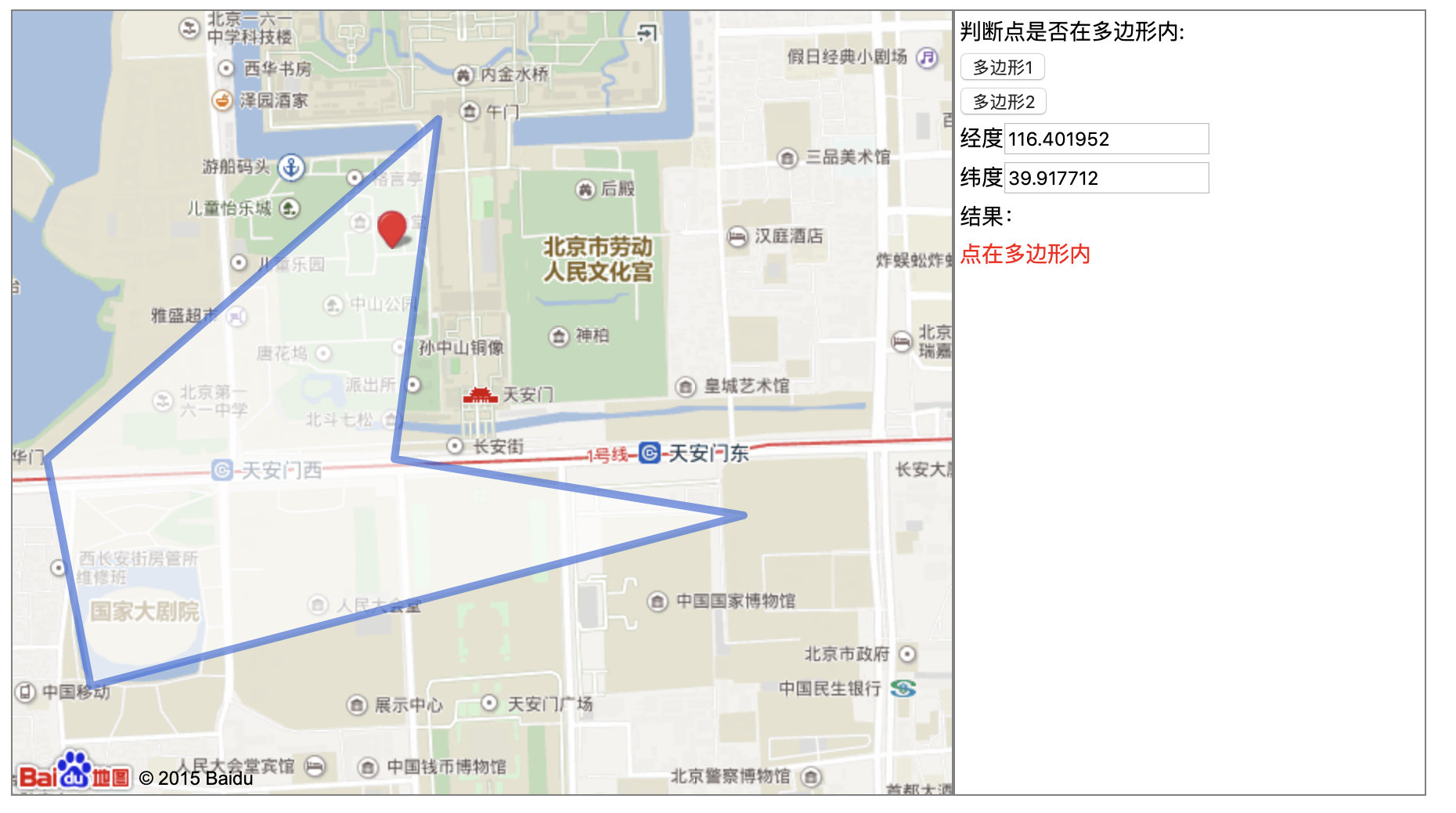
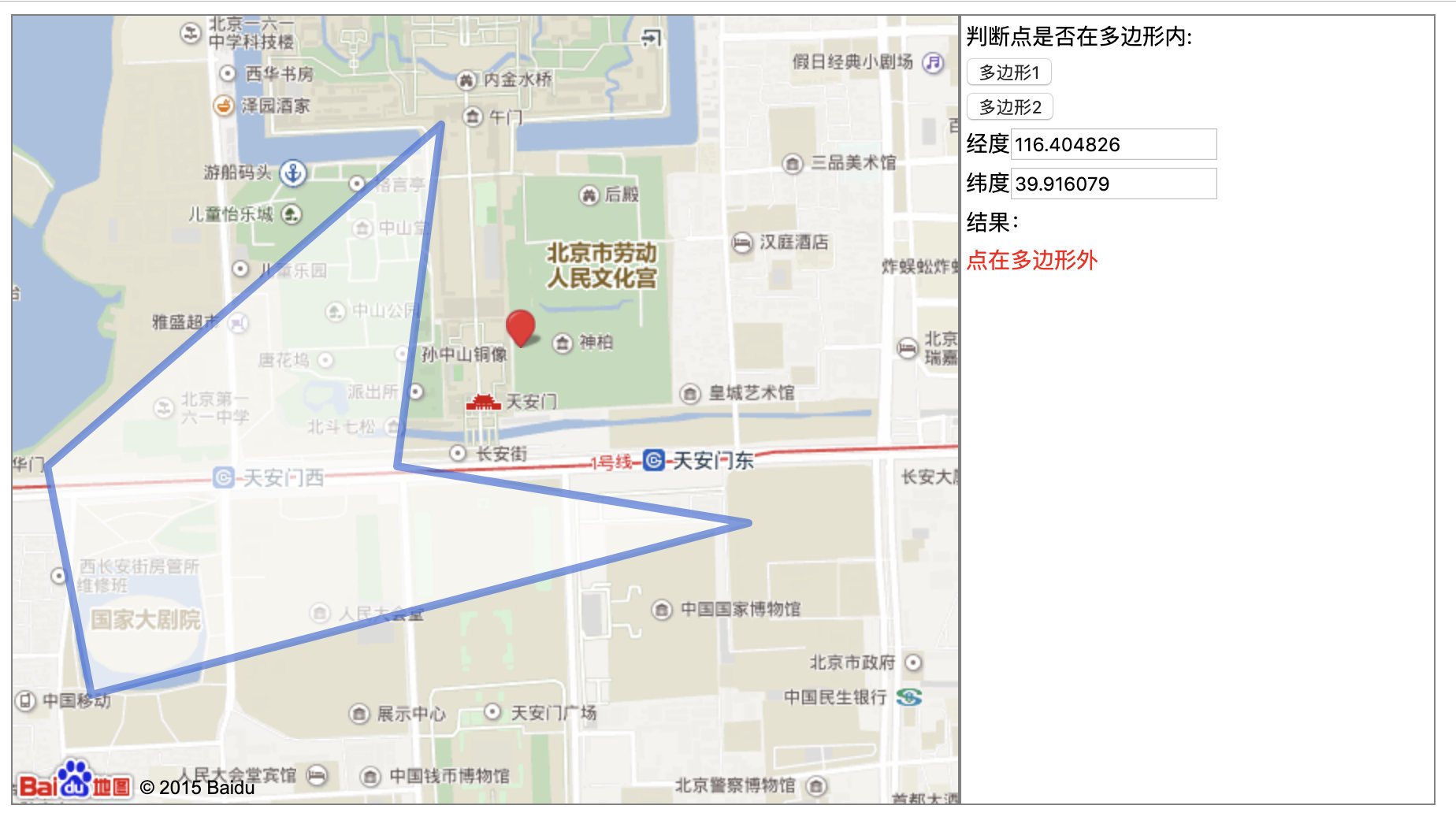
后台的测试方法:
// 测试一个点是否在多边形内
public static void main(String[] args) {
Point2D.Double point = new Point2D.Double(116.404072, 39.916605);
List<Point2D.Double> pts = new ArrayList<Point2D.Double>();
pts.add(new Point2D.Double(116.395, 39.910));
pts.add(new Point2D.Double(116.394, 39.914));
pts.add(new Point2D.Double(116.403, 39.920));
pts.add(new Point2D.Double(116.402, 39.914));
pts.add(new Point2D.Double(116.410, 39.913));
if (IsPtInPoly(point, pts)) {
System.out.println("点在多边形内");
} else {
System.out.println("点在多边形外");
}
}
经过测试,结果满意。
总结,实现的过程最重要是保存那些顶点,并根据那些保存的顶点(有一定的顺序),来判断一个点是否在这些顶点围成的多边形内。
感觉百度地图还是很好用的。API很全,而且都配有demo,非常利于我们开发者。