物流配送路径优化问题分析与算法解读(一)
去年五一跳蚤以后,一直在一家公司参与物流配送软件开发的相关工作,负责的工作内容包括物流配送路径优化这一块。关于物流配送这一专业领域,自己以前也是门外汉,对这一领域也没有接触过,更谈不上理解。所以,一直在学习,一直在探索。在这个过程中因为工作需要学习了很多大牛的博客(太多了,记不住,所以大家别指望了,还是踏实看我的帖子吧),也研究了在开发过程中客户提出的物流配送路径优化领域的相关需求(因为客户来头较权威,需求比较专业,所以问题很具有代表性),有所收获。好东西当然要拿出来与大家分享。我会把这段时间的学习和研究所得整理成一个系列(好吧,真心有点装,不过思考了一下,发现要写的确实不少),欢迎大家批评指正。另外,在这个过程中,我还使用了大量的谷歌地图API技术,也有所积累,如果大家有需求,发帖顶起啊,我也可以找个时间整理出来与大家分享!如果遇上同行,还请不吝赐教。
在这个系列里,我会按照从易到难,从简单到复杂的顺序,向大家分类,分级逐步介绍物流配送路径优化过程中的问题。
今天先起一个头,这也是一切物流配送路径优化问题的起点,那就是旅行商问题。相信阅读这篇文章的同学应该对旅行商问题有所了解,我就不赘述了。
我将物流配送领域中的旅行商问题归纳如下:
物流企业A在B市有一个配送中心,有M个固定的配送客户。企业A每天需要为这M个客户配送一定量的货物。现在,有这样一个问题,要求企业A派出一辆车配送所有客户,不考虑车辆载重与结点需求,且该辆车不管如何行驶,均能够一次性配送完所有客户,现在只需考虑一个问题,那就是如何行车才能保证所有点均已配送且只配送一次,且总的行车路径最短。这是典型的TSP问题,也是物流配送路径优化问题中最基本和最简单的问题。
目前针对该问题,有很多的解决方法,包括有名的蚁群算法,包括遗传算法等等,这些都能够有效的获取相对最优解。我只捡我实践过且目前运行良好的几种算法来说:
1、扫描法
(1)原理介绍:
(1)原理介绍:
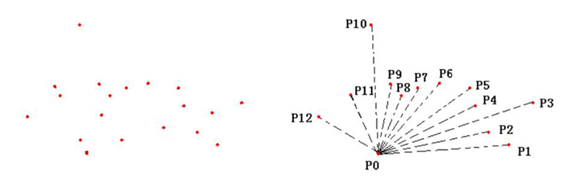
如上图所示,P0为起始点,其它点为配送需求点。采用极坐标来表示各点的相对位置,然后以P0点为坐标原点,以P1为起始点,定其角度为零度,以顺时钟或逆时钟方向开始扫描各个点,获得各点与原点连线P0Pn相对于P0P1的角度大小。根据角度大小确定其顺序,直至扫描完毕。扫描结束后获得的点的序列就是各点的配送顺序。
(2)结果分析:
简单扫描法并不能保证获取最短路径。但是其算法原理简单,执行效率高,而且所获取的结果与最优路径之间的偏差较小。
2、分支界定法
(1)原理介绍:
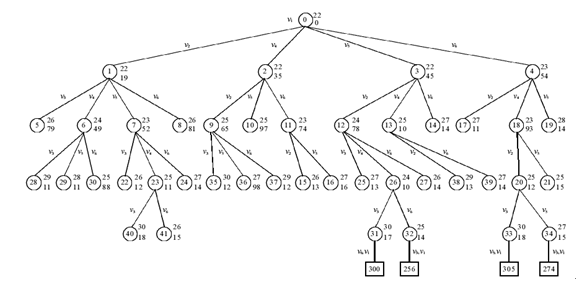
分支限界法又称为剪枝限界法或分支定界法,它类似于回溯法,也是一种在问题的解空间树T上搜索问题解的算法。它与回溯法有两点不同:
①回溯法只通过约束条件剪去非可行解,而分支限界法不仅通过约束条件,而且通过目标函数的限界来减少无效搜索,也就是剪掉了某些不包含最优解的可行解。
②在解空间树上的搜索方式也不相同。回溯法以深度优先的方式搜索解空间树,而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间树。
分支限界法的搜索策略是:在扩展结点处,先生成其所有的子结点(分支),然后再从当前的活结点表中选择下一个扩展结点。为了有效地选择下一扩展结点,以加速搜索的进程,在每一活结点处,计算一个函数值(限界),并根据这些已计算出的函数值,从当前活结点表中选择一个最有利的结点作为扩展结点,使搜索朝着解空间树上有最优解的分支推进,以便尽快地找出一个最优解。从活结点表中选择下一扩展结点的不同方式导致不同的分支限界法。最常见的有以下两种方式:
①队列式(FIFO)分支限界法:队列式分支限界法将活结点表组织成一个队列,并按队列的先进先出原则选取下一个结点为当前扩展结点。
②优先队列式分支限界法:优先队列式分支限界法将活结点表按照某个估值函数C(x)的值组织成一个优先队列,并按优先队列中规定的结点优先级选取优先级最高的下一个结点成为当前扩展结点。
(2)结果分析:
分支界定法能获取最短路径。
分支限界法常以广度优先或以最小耗费(最大效益)优先的方式搜索问题的解空间树。在分支限界法中,每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点,就一次性产生其所有儿子结点。在这些儿子结点中,导致不可行解或导致非最优解的儿子结点被舍弃,其余儿子结点被加入活结点表中。
此后,从活结点表中取下一结点成为当前扩展结点,并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止。
影响分支限界法搜索效率的有两个主要因素:一是优先队列Q的优先级由C(x)确定,它能否保证在尽可能早的情况下找到最优解,如果一开始找到的就是最优解,那么搜索的空间就能降低到最小;二是限界函数u(x),它越严格就越可能多地剪去分支,从而减少搜索空间。
在用分支限界法解决TSP问题时,有不少很好的限界函数和估值函数已经构造出来出了,使得分支限界法在大多数情况下的搜索效率大大高于回溯法。但是,在最坏情况下,该算法的时间复杂度仍然是O(n!),而且有可能所有的(n-1)!个结点都要存储在队列中。
3、蚁群算法
(1)原理介绍:
(1)原理介绍:
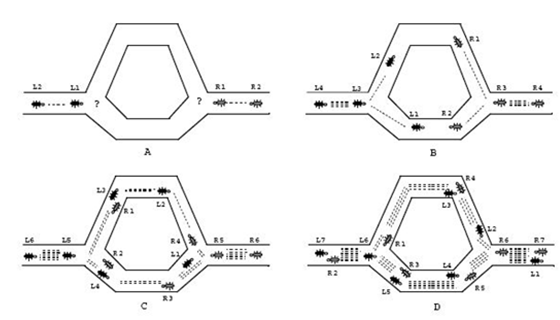
意大利学者M.Dorigo,V.Maniezzo等人在观察蚂蚁的觅食习性时发现,蚂蚁总能找到巢穴与食物源之间的最短路径。经研究发现,蚂蚁的这种群体协作功能是通过一种遗留在其来往路径上的叫做信息素(Pheromone)的挥发性化学物质来进行通信和协调的。化学通信是蚂蚁采取的基本信息交流方式之一,在蚂蚁的生活习性中起着重要的作用。通过对蚂蚁觅食行为的研究,他们发现,整个蚁群就是通过这种信息素进行相互协作,形成正反馈,从而使多个路径上的蚂蚁都逐渐聚集到最短的那条路径上。
这样,M.Dorigo等人于1991年首先提出了蚁群算法。其主要特点就是:通过正反馈、分布式协作来寻找最优路径。这是一种基于种群寻优的启发式搜索算法。它充分利用了生物蚁群能通过个体间简单的信息传递,搜索从蚁巢至食物间最短路径的集体寻优特征,以及该过程与旅行商问题求解之间的相似性。得到了具有NP难度的旅行商问题的最优解答。
其求解过程可以形象的解释如下:
如上图所示,蚂蚁在最开始的时候因为障碍物阻挡,不得不延上下两条路绕行。上面的路径比下面的路径要长。我们假设所有蚂蚁的运动速度一样,那么在单位时间里通过下面路径的蚂蚁数量在概率上说,显然要比从上面通过的蚂蚁数量要多。因为蚂蚁的移动过程中会产生信息素,我们假设每只蚂蚁单位时间内产生的信息素是一定的,那么下面路径的信息素浓度显然要大于上面的路径。随着时间的增加,这种差别越来越大,而蚂蚁之间是通过信息素来传递信息的,所以越来越多的蚂蚁因为蚂蚁浓度的影响,从下面的路径通过,直至最后绝大多数的蚂蚁都从下面的路经过。
蚁群算法是一种正反馈的算法。从真实蚂蚁的觅食过程中我们不难看出,蚂蚁能够最终找到最短路径,直接依赖于最短路径上信息激素的堆积,而信息激素的堆积却是一个正反馈的过程。对蚁群算法来说,初始时刻在环境中存在完全相同的信息激素,给予系统一个微小扰动,使得各个边上的轨迹浓度不相同,蚂蚁构造的解就存在了优劣,算法采用的反馈方式是在较优的解经过的路径留下更多的信息激素,而更多的信息激素又吸引了更多的蚂蚁,这个正反馈的过程使得初始的不同得到不断的扩大,同时又引导整个系统向最优解的方向进化。因此,正反馈是蚂蚁算法的重要特征,它使得算法演化过程得以进行。
(2)结果分析:
蚁群算法并不能保证一定可以获取最短路径。但是通过修改其算法因子,我们能够得到最优近似解。如果对其进行多次循环处理,从得到的一组最优近似解中筛选出的最小值,一般就是最优解。
4、三种算法对比
|
算法名称 |
时间复杂度 |
空间复杂度 |
优点 |
缺点 |
|
简单扫描法 |
n (n表示结点个数) |
n (n表示结点个数) |
运算速度快,执行效率高。 |
求解结果不一定是最优解。 |
|
分支界定法 |
n! (n表示结点个数) |
(n-1)! (n表示结点个数) |
能够求得最优解。 |
运算时间长,对内存空间要求大,如果求解空间太大,容易导致内存溢出。 |
|
蚁群算法 |
k*m*n (k表示循环次数,m表示蚂蚁个数,n表示结点个数) |
m*n (m表示蚂蚁个数,n表示结点个数) |
采用分布式计算,具有较强的鲁棒性,可以通过控制算法因子对结果进行优化。多次循环能够得到最优近似解。 |
运算时间长,信息素增量有可能导致错误的引导。算法因子确定难。 |