1. 最优停止理论 - 如何选择停止观望的时机
也就是最优停止问题(源于“秘书问题”),答案很简单,就是37%(其实是1/e, 35%-40%)。最优停止问题有男性选择约会对象、女性挑选求婚者、租房等。
在所有的最优停止问题中,最大的难点不在于选择哪一种可选方案,而是确定自己需要考虑多少种方案。
遵循这个法则,一般取得最理想结果的可能性就非常接近于最高值。
2. 每种文化的社会偏爱都会对社会的形式系统产生影响。
例如,在我们的心中国际象棋是中世纪欧洲人的象征,但是实际上国际象棋起源于8世纪的印度。
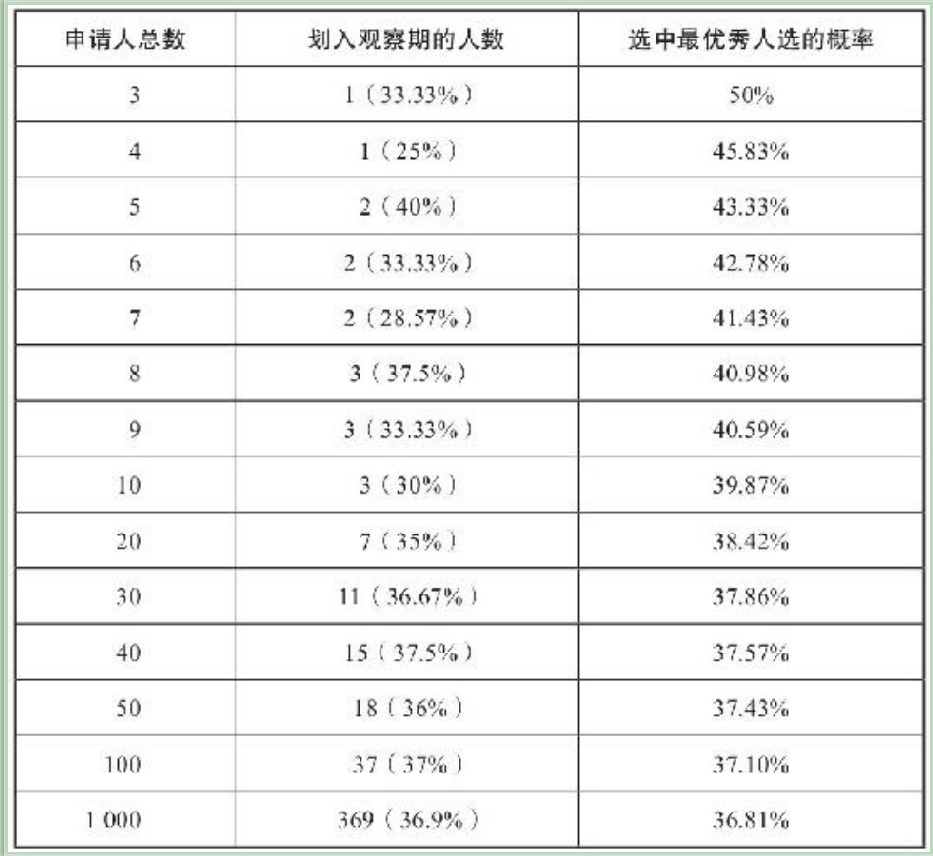
3. 具体的37法则,从观察期切换到行动期的时间点一般在37%左右
在考察前37%的申请人时,不要接受任何人的申请。然后,只要任何一名申请人比前面所有人选有优秀,就要后不犹豫地选择他/她。
就像做软件技术选型时候,过了观察期,马上行动。
奇怪的数学对称性。
4. 37%法则有灵活性。
既可以表示申请者的人数,也可以表示过程持续的时间。
无信息博弈的成功率在37%以下,全信息博弈的成功率大于37%。个人认为这是一般情况,收敛、回归到37%。
5. 观望期转变到阈值准则。
假如掌握的信息够多,直接跳过观望期,定一个阈值。
直接接受第一个高于阈值的报价。
另外,买家喜欢积极的卖家,因为到极限时,会降低标准、期望。
6. 最优选择问题,随着时间的流逝,会变成最优停止问题。
所以要抓住现在,抓住每一天,让我们的生活变的非凡起来。
最优选择需要穷举所有选择,注意权衡,然后选择最好的。但是时间不允许这样做。所以最优停止很重要。
7. 阈值的设定取决于成本。
例如金钱、时间。
8. 回头在大多数情况下是不明智的。
因为已经付出的已经成为了成本。
9. 免费才是最贵的。
因为除了金钱,也有成本要考虑。
例如,理想的停车位应该标价,这是行走所需时间、造成麻烦(交通堵塞)、寻找停车位所需时间、油耗、车内乘客数等方面实现优化并精确平衡。
如果停车费低甚至免费,可能的情况是为了找到一个停车位,结果既浪费时间又浪费汽油。
重点: 停车问题不是单纯靠增加资源(停车位)并最大化利用资源(占用)就可以解决的。停车问题是一个进程(是一个最优停止问题),消耗注意力、时间、汽油,还会导致污染和拥堵等后果。合适的政策可以解决这个问题。
10. 要分清是不是最优停止问题。
例如玩一个游戏:“从1美元开始,要么三倍,要么赔光”。这个没有合适的最优停止准则。
第一轮,有一般机会赢得3美元,一般机会0美元,期望是1.5美元。第二轮:期望是4.5美元。如果根据这个数学计算,应该一直玩下去。或者说,期望值不是最终目标。
11. 探索与利用。
它们之间存在取舍的问题。
12. 大O符号
大O符号的目的不是使用分钟和秒去表示算法的性能,而是讨论问题规模的程序运行时间之间的关系。