20182307 2019-2020-1 《数据结构与面向对象程序设计》第十周学习总结
目录
教材学习内容总结
- 第十九章 图 主要介绍了另一种非线性数据结构:图。与树不同的是,图没有特定的父子关系,图中的结点可以与许多其他的结点相连接,所以从另一个角度来说,树就是图。本章从图的两种分类:无向图与有向图介绍起,解释了各自的概念与异同,并扩展知识应用,延伸出了如广度优先遍历、深度优先遍历、带权图、最小生成树等知识。
学习笔记
- 无向图
- 表示边的顶点对是无序的
- 如果图中两个顶点之间有边连接,则称它们是邻接的
- 含有最多条边的无向图成为完全图
- 无向图中的路径是双向的
- 若无向图中任意两个顶点间都有路径,则无向图称为连通的
- 有向图
- 边是顶点的有序对
- 有向图中的路径是连接图中两个顶点的有向边的序列
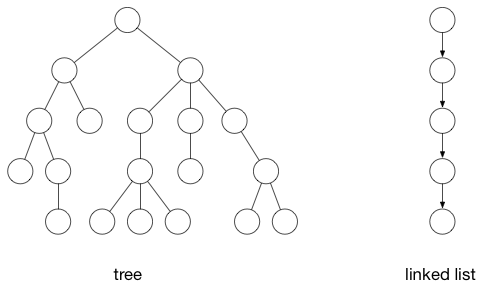
- 带权图
- 每条边上都对应一个权值的图
- 应用:计算最小路径;构建最小生成树
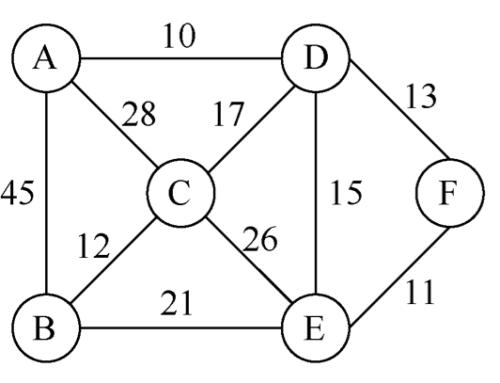
- 遍历方式
- 广度优先遍历
- 类似于树的层序遍历
- 深度优先遍历
- 类似于树的先序遍历
- 图的深度优先遍历与广度优先遍历的主要差别在于用栈代替队列来管理遍历过程
- 广度优先遍历
- 测试连通性
- 当且仅当从任意顶点开始的广度优先遍历中得到的顶点数等于图中所含的顶点数时,图是连通的
- 最小生成树
- 生成树是包含图中所有顶点及图中部分(可能不是全部)边的一棵树
- 最小生成树是其所含边的权值之和小于等于图的任意其他生成树的边的权值之和的生成树
- 邻接矩阵
- 用一个二维数组的每个位置表示图中两个顶点的交叉点,在每个这样的交叉点用一个布尔值来表示两个顶点是否邻接
教材学习中的问题和解决过程
- 问题1:如何理解广度优先遍历与深度优先遍历?他们的实现方法有什么不同?区别有哪些?
- 书本内容:图的深度优先遍历与广度优先遍历的主要差别在于用栈代替队列来管理遍历过程
- 个人理解:
- 首先从字面理解,广度遍历的特点就是每次从一个比较大的范围来遍历结点,而深度遍历的特点是每次先优先走完某个完整的路径,并访问该路径上的点。举例来通俗理解就是,广度遍历就像投一枚石子入水,通过一圈圈的涟漪来访问一定的范围,而深度遍历就像一台扫地机器人,前方遇到障碍(即遍历某分支到底)才会折返。
- 书本内容中提到,图的深度优先遍历与广度优先遍历的主要差别在于用栈代替队列来管理遍历过程,这就涉及具体实现层次了。
- 深度遍历的大致实现思路是:把根节点压入栈中。每次从栈中弹出一个元素,搜索所有在它下一级的元素,把这些元素压入栈中。并把这个元素记为它下一级元素的前驱。找到所要找的元素时结束程序。如果遍历整个树还没有找到,结束程序。
- 广度遍历的大致实现思路是:把根节点放到队列的末尾。每次从队列的头部取出一个元素,查看这个元素所有的下一级元素,把它们放到队列的末尾。并把这个元素记为它下一级元素的前驱。找到所要找的元素时结束程序。如果遍历整个树还没有找到,结束程序。
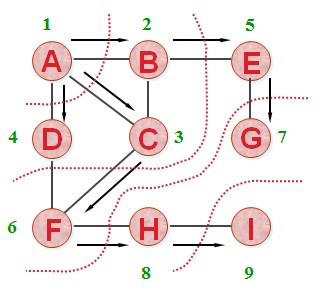
- 问题2:如何将图改造成最小生成树?
- 书本内容:最小生成树是其所含边的权值之和小于等于图的任意其他生成树的边的权值之和的生成树
- 个人理解:
- 先不论从代码层次实现。如果要想将一张图转换为一棵最小生成树,可以考虑应用离散数学中学习过的“破圈法”。即寻找图中所有由数条边构成的闭合圈,删除权值最大的那条边,反复进行此操作,直到每个“圈”都被破去。
- 代码实现方面,首先选择任一结点为起点,再将包含起始点的所有边按权值大小加入最小堆中,然后删除最小堆中的边,并将这条边和新的结点加入到最小生成树中,重复此过程直到最小生成树中包含所有结点或最小堆为空。
代码调试中的问题和解决过程
- 问题1:在做课后习题PP19_3时,不知道怎么实现最小路径的程序
- 解决方案:
- 网络资料:Dijkstra算法之 Java详解
- 详解Dijkstra算法
- 初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为"起点s到该顶点的距离"[例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞]
- 从U中选出"距离最短的顶点k",并将顶点k加入到S中;同时,从U中移除顶点k
- 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离
- 重复步骤(2)和(3),直到遍历完所有顶点
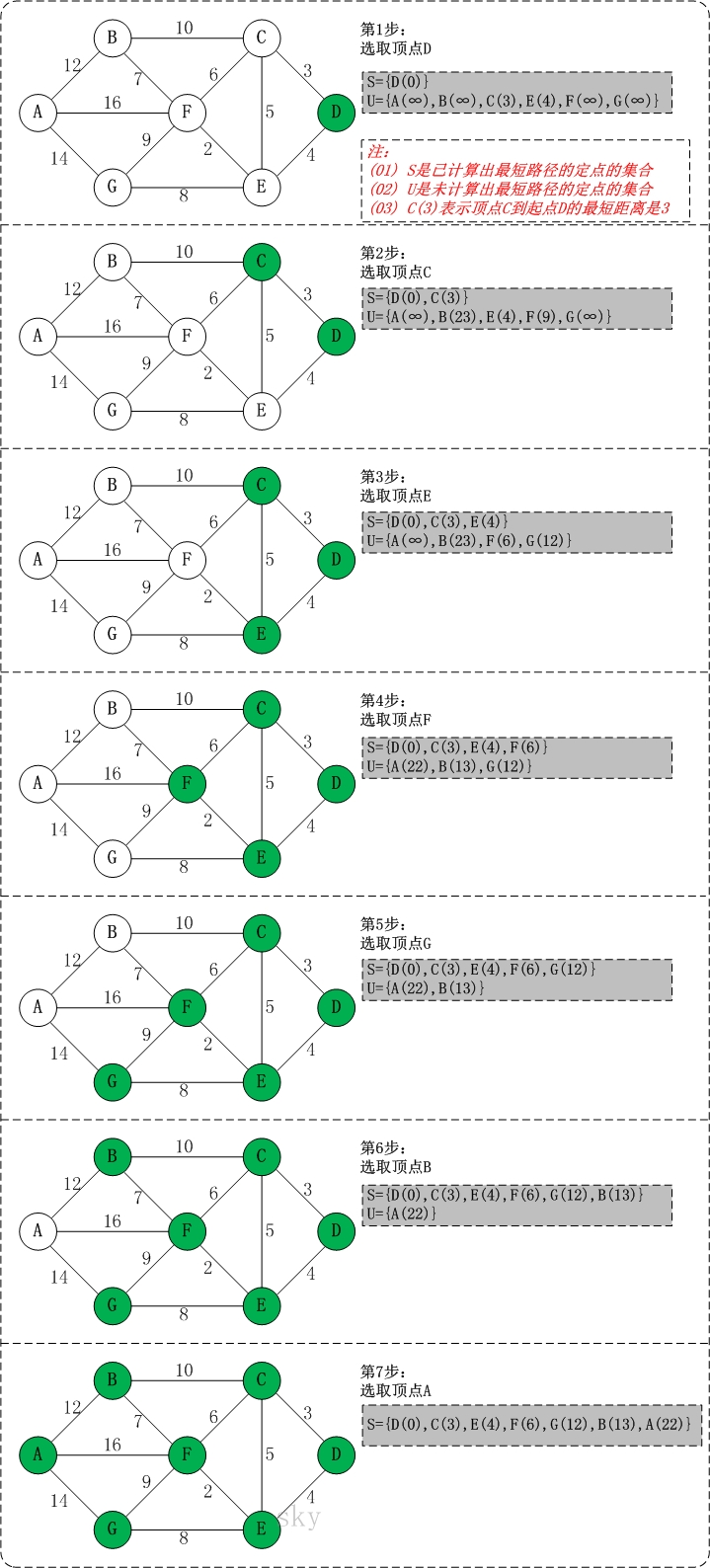
- 解决方案:
代码托管

上周考试错题总结
- 错题1:
Insertion sort is an algorithm that sorts a list of values by repetitively putting a particular value into its final, sorted, position.
A . true
B . false
- 原因分析:没有注意到句末的"final",插入算法是将元素插入之前的列表中的。
- 理解情况:插入排序是一种排序算法,通过反复地把某个元素插入到之前已排序的子列表中,实现元素的排序。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 10000行 | 30篇 | 400小时 | |
| 第一周 | 209/209 | 2/2 | 9/9 | |
| 第二、三周 | 290/499 | 2/4 | 18/28 | |
| 第四周 | 516/1015 | 2/6 | 22/50 | |
| 第五周 | 2981/3996 | 2/8 | 32/82 | |
| 第六周 | 1498/5494 | 2/10 | 20/102 | |
| 第七周 | 1519/7013 | 2/12 | 51/153 | |
| 第八周 | 1641/8654 | 2/14 | 21/174 | |
| 第九周 | 2451/11105 | 2/16 | 30/204 | |
| 第十周 | 2023/13128 | 2/18 | 49/253 |