L1-049 天梯赛座位分配 (20 分)
稳妥起见,模拟题还是用最真实的模拟来写比较好

#include "bits/stdc++.h" using namespace std; const int maxn = 1100; vector<int> q[maxn]; vector<int> ans[maxn]; int main() { freopen("input.txt", "r", stdin); int n; cin >> n; int k; int slove = 0, cnt = 0, all = 0; for (int i = 1; i <= n; i++) { cin >> k; all += k * 10; for (int j = 1; j <= k * 10; j++) { q[i].push_back(1); } } int now = 1, last = 0; while (slove < all) { for (int i = 1; i <= n; i++) { if (!q[i].empty()) { if (last == i) now = 2; cnt += now; q[i].pop_back(); ans[i].push_back(cnt); slove++; last = i; } } } for (int i = 1; i <= n; i++) { printf("#%d ", i); int flag = 0; for (int j = 0; j < ans[i].size(); j++) { if (flag) printf(" "); flag = 1; printf("%d", ans[i][j]); if ((j + 1) % 10 == 0) printf(" "), flag = 0; } } return 0; }
L2-4 秀恩爱分得快 (25 分)
太傻屌了。
一个坑,0在是女性的时候是-0,但是用int会区分不出来,要用字符串读。
傻屌就傻屌在,我只想到了读入,输出的时候还是直接乘上sex就输出了。。。 -1*0还是0.。。 WA了半天。
还有一个点就是它问的那对情侣中可能有人根本就没在照片中出现过。。。。。。。

#include "bits/stdc++.h" using namespace std; const int maxn = 1100; double ans[maxn][maxn]; int mp[maxn][maxn]; int sex[maxn]; int main() { freopen("input.txt", "r", stdin); int n, m; cin >> n >> m; int from, flag; string s, t; for (int i = 0; i < m; i++) { cin >> mp[i][0]; for (int j = 1; j <= mp[i][0]; j++) { cin >> s; mp[i][j] = abs(stoi(s)); sex[mp[i][j]] = (s[0] == '-' ? -1 : 1); } } int a, b; cin >> s >> t; a = abs(stoi(s)); sex[a] = (s[0] == '-' ? -1 : 1);//WA的倒数第二个点 b = abs(stoi(t)); sex[b] = (t[0] == '-' ? -1 : 1); double maxa = 0, maxb = 0; for (int i = 0; i < m; i++) { for (int j = 1; j <= mp[i][0]; j++) { if (mp[i][j] == a) { for (int k = 1; k <= mp[i][0]; k++) { if (sex[a] != sex[mp[i][k]]) { ans[a][mp[i][k]] += 1.0 / mp[i][0]; } maxa = max(maxa, ans[a][mp[i][k]]); } } if (mp[i][j] == b) { for (int k = 1; k <= mp[i][0]; k++) { if (sex[b] != sex[mp[i][k]]) ans[b][mp[i][k]] += 1.0 / mp[i][0]; maxb = max(maxb, ans[b][mp[i][k]]); } } } } if (ans[a][b] == maxa && ans[b][a] == maxb) { if (sex[a] == -1) cout << "-";//WA的倒数第二个点 cout << a << " "; if (sex[b] == -1) cout << "-"; cout << b << endl; } else { for (int i = 0; i < n; i++) { if (sex[i] != sex[a] && ans[a][i] == maxa) { if (sex[a] == -1) cout << "-"; cout << a << " "; if (sex[i] == -1) cout << "-"; cout << i << endl; } } for (int i = 0; i < n; i++) { if (sex[i] != sex[b] && ans[b][i] == maxb) { if (sex[b] == -1) cout << "-"; cout << b << " "; if (sex[i] == -1) cout << "-"; cout << i << endl; } } } return 0; }
L3-020 至多删三个字符 (30 分)
dp[i][j]表示到第i个字符已经删除了j个。

#include "bits/stdc++.h" using namespace std; typedef long long ll; const int maxn = 1e6 + 100; ll dp[maxn][5]; char str[maxn]; int main() { freopen("input.txt", "r", stdin); cin >> str; int len = strlen(str); dp[1][1] = dp[2][2] = dp[3][3] = dp[1][0] = dp[2][0] = dp[3][0] = 1; for (int i = 2; i <= len; i++) { dp[i][0] = dp[i - 1][0]; if (str[i - 1] == str[i - 2]) { dp[i][1] = dp[i - 1][1] + dp[i - 1][0] - 1; dp[i][2] = dp[i - 1][1] + dp[i - 1][2] - dp[i - 2][1]; dp[i][3] = dp[i - 1][2] + dp[i - 1][3] - dp[i - 2][2]; } else if (i >= 3 && str[i - 1] == str[i - 3]) { dp[i][1] = dp[i - 1][0] + dp[i - 1][1]; dp[i][2] = dp[i - 1][1] + dp[i - 1][2] - dp[i - 2][0]; dp[i][3] = dp[i - 1][2] + dp[i - 1][3] - dp[i - 3][1]; } else { dp[i][1] = dp[i - 1][0] + dp[i - 1][1]; dp[i][2] = dp[i - 1][1] + dp[i - 1][2]; dp[i][3] = dp[i - 1][2] + dp[i - 1][3]; if (i >= 4 && str[i - 1] == str[i - 4]) { dp[i][3]--; } } } ll ans = 0; for (int i = 0; i <= 3; i++) ans += dp[len][i]; cout << ans << endl; return 0; }
L3-021 神坛 (30 分)
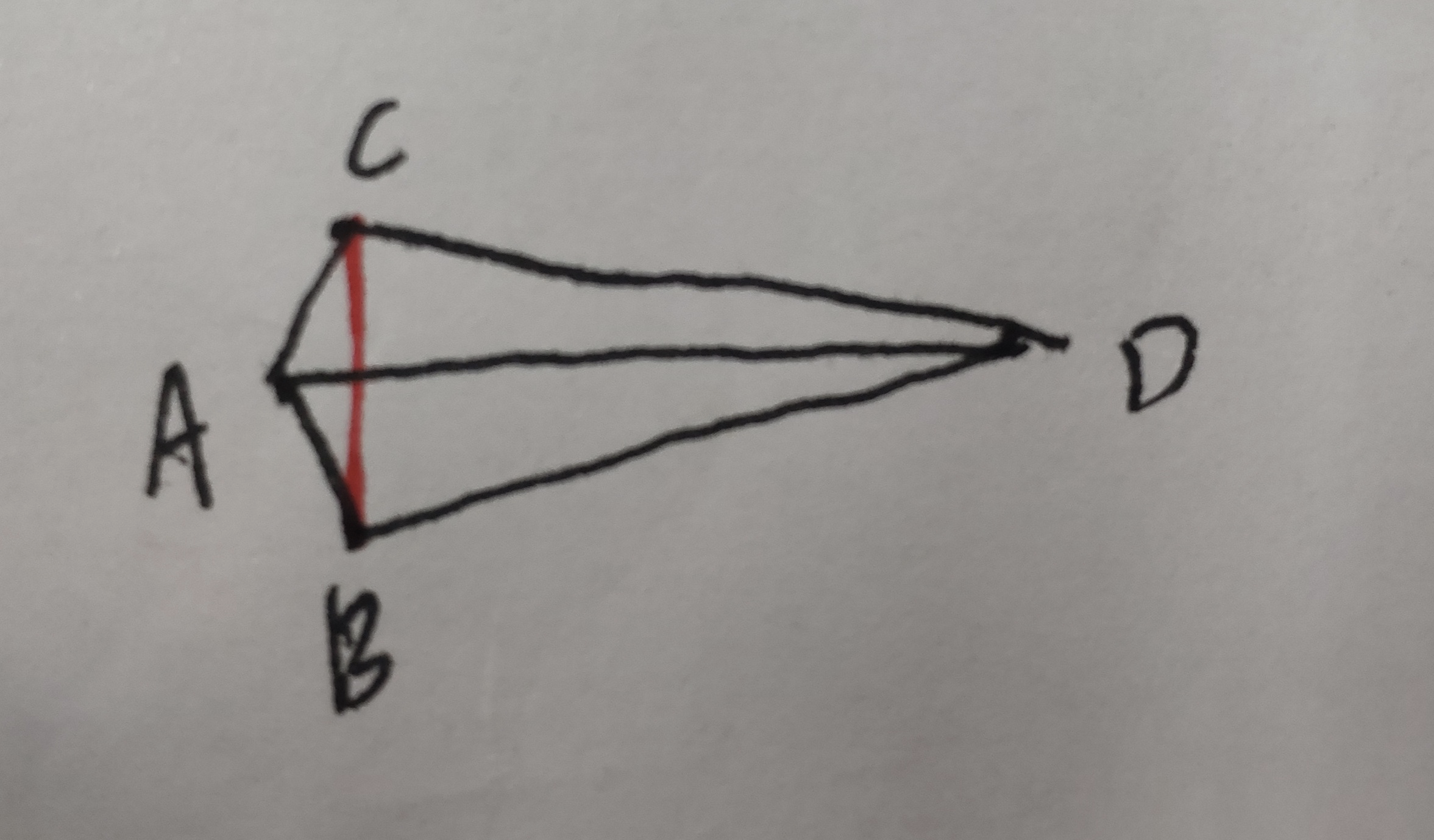
三角形面积等于三个点形成的两个向量的叉乘的1/2。
主要的问题在于如何降低复杂度。
枚举n个点,对于每个点求出其他所有点与他形成的向量,然后按照极角排序,对于每两个相邻的向量,求其代表的三角形的面积,去最小值即得答案。
假设有ABCD四个点,在以A为顶点时可以求出ABD与ACD的面积,但显然ABC的面积最小,这并不影响求出答案,因为在以C或B为顶点时,可以求到ABC的面积。

#include "bits/stdc++.h" using namespace std; typedef long long ll; const int maxn = 3e6; struct node { ll x, y; } e[maxn], c[maxn]; bool cmp(node a, node b) { return a.y * b.x > b.y * a.x; } int main() { int n; cin >> n; for (int i = 0; i < n; i++) { cin >> e[i].x >> e[i].y; } int cnt; ll ans = 1ll << 62; for (int i = 0; i < n; i++) { cnt = 0; for (int j = 0; j < n; j++) { if (i != j) { c[cnt].x = e[j].x - e[i].x; c[cnt++].y = e[j].y - e[i].y; } } sort(c, c + cnt, cmp); for (int j = 1; j < cnt; j++) { ans = min(ans, abs(c[j].x * c[j - 1].y - c[j - 1].x * c[j].y)); } } printf("%.3f ", ans / 2.0); return 0; }
