1.
2.
3.
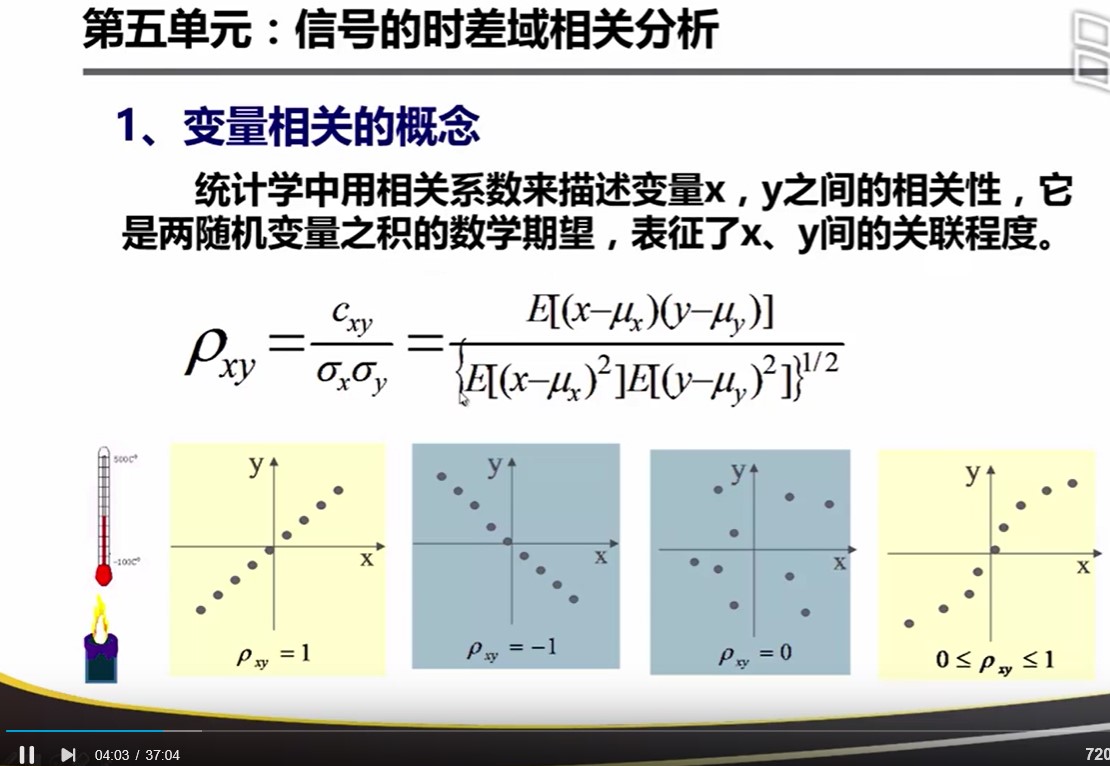
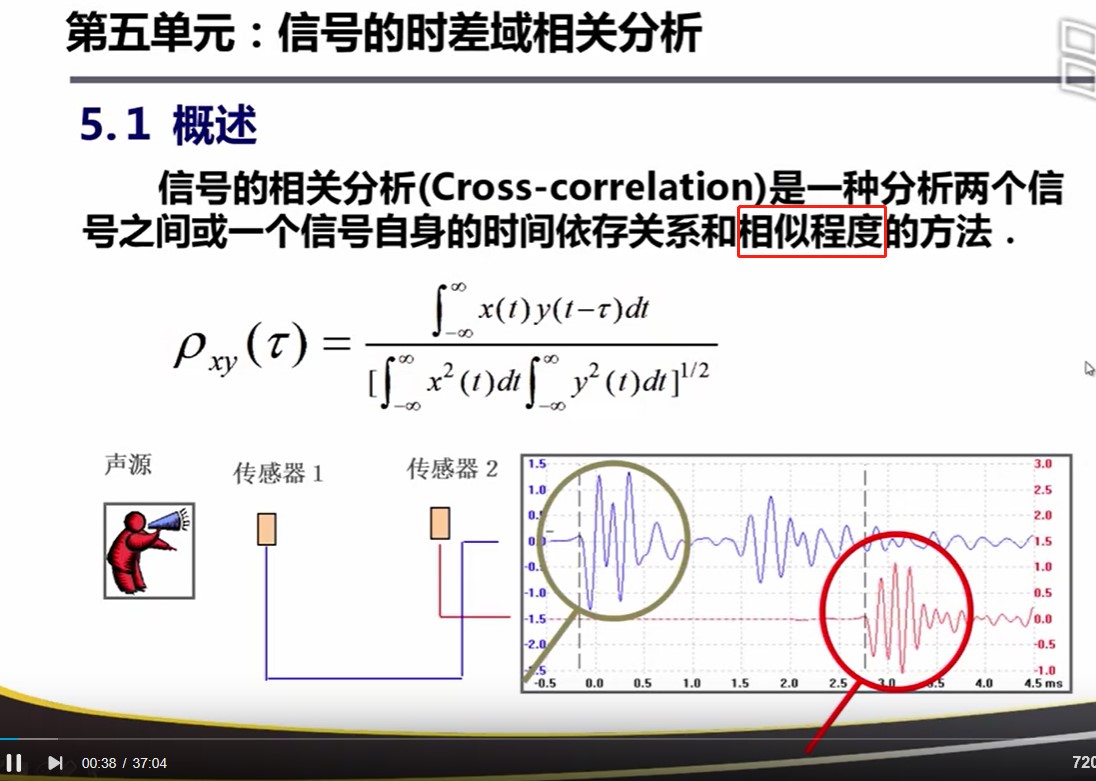
正相关、负相关、无关、
4.
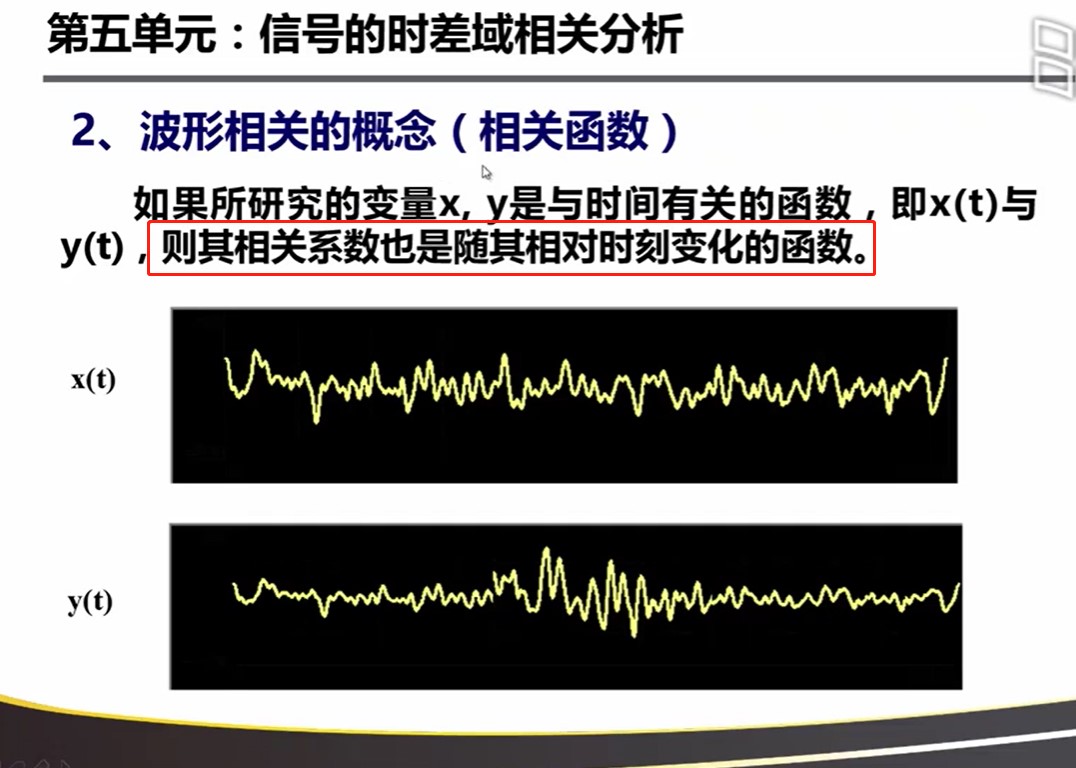
5.
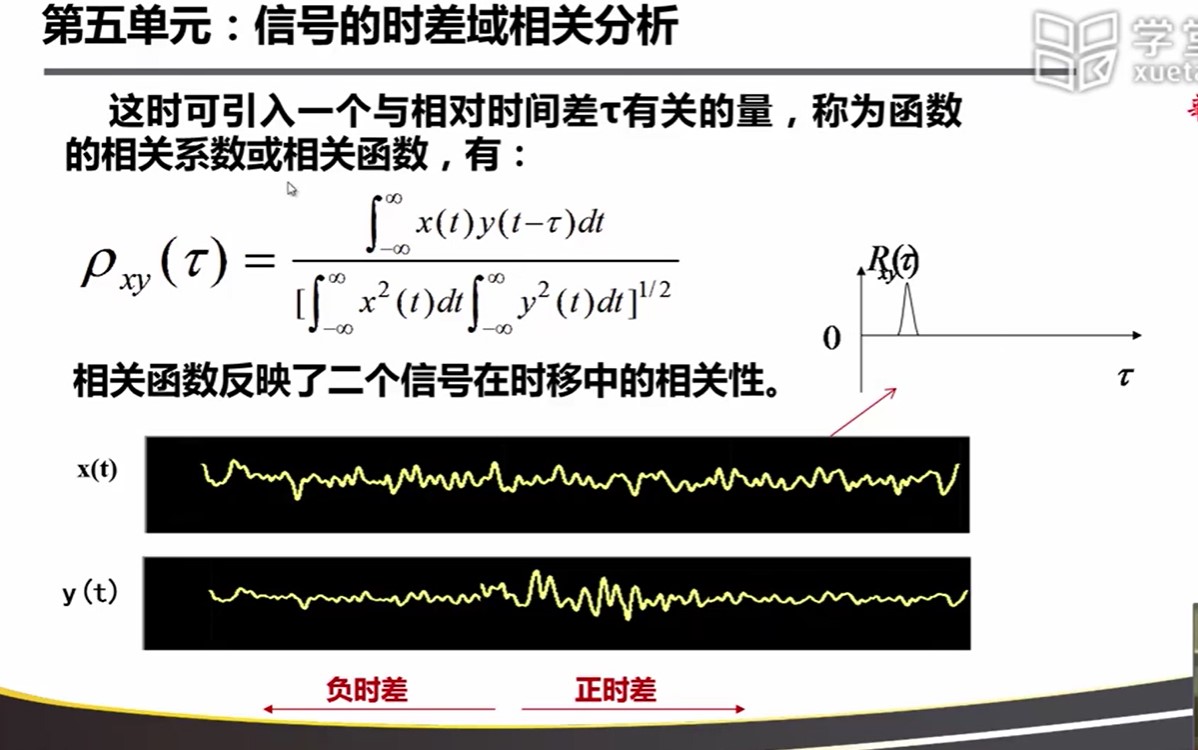
tao 变化时,会有一个相关函数的曲线
6.

7.

相关曲线的中心点是它的对称点
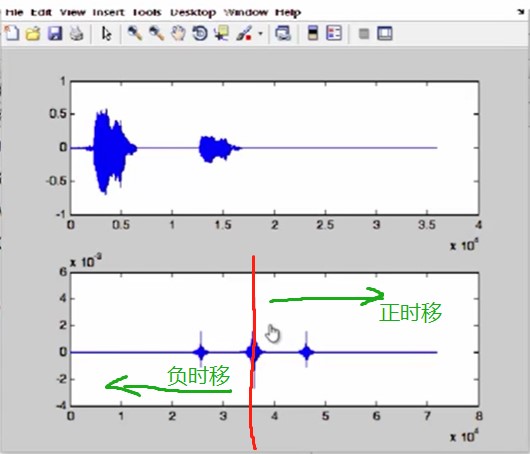
8.
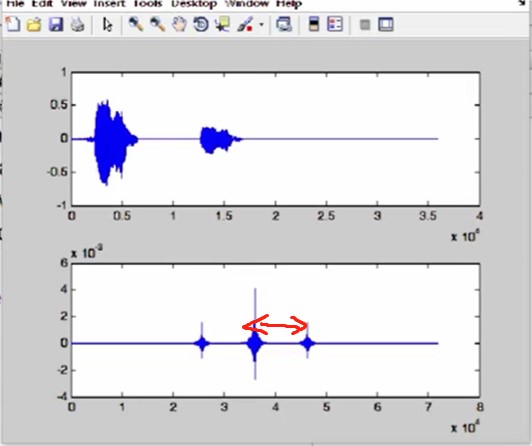
这两个峰值之间的时间差就是我们想得到的那个时间差。
9.
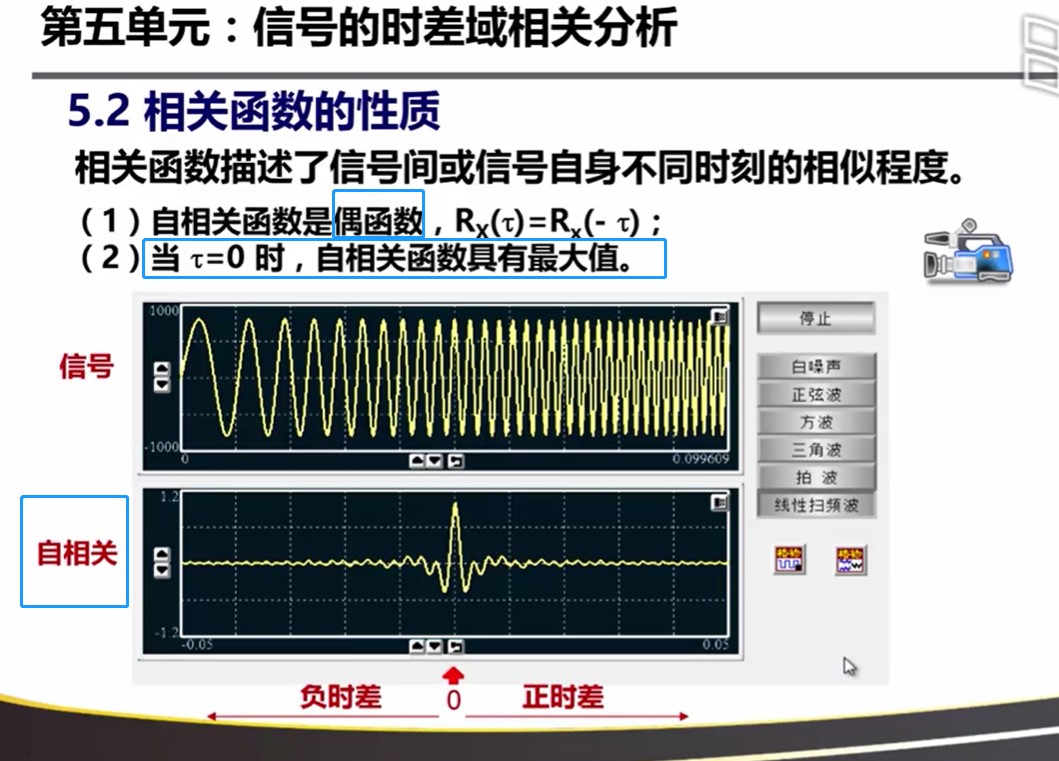

周期函数的自相关函数丢失了相位信息
10.
11.
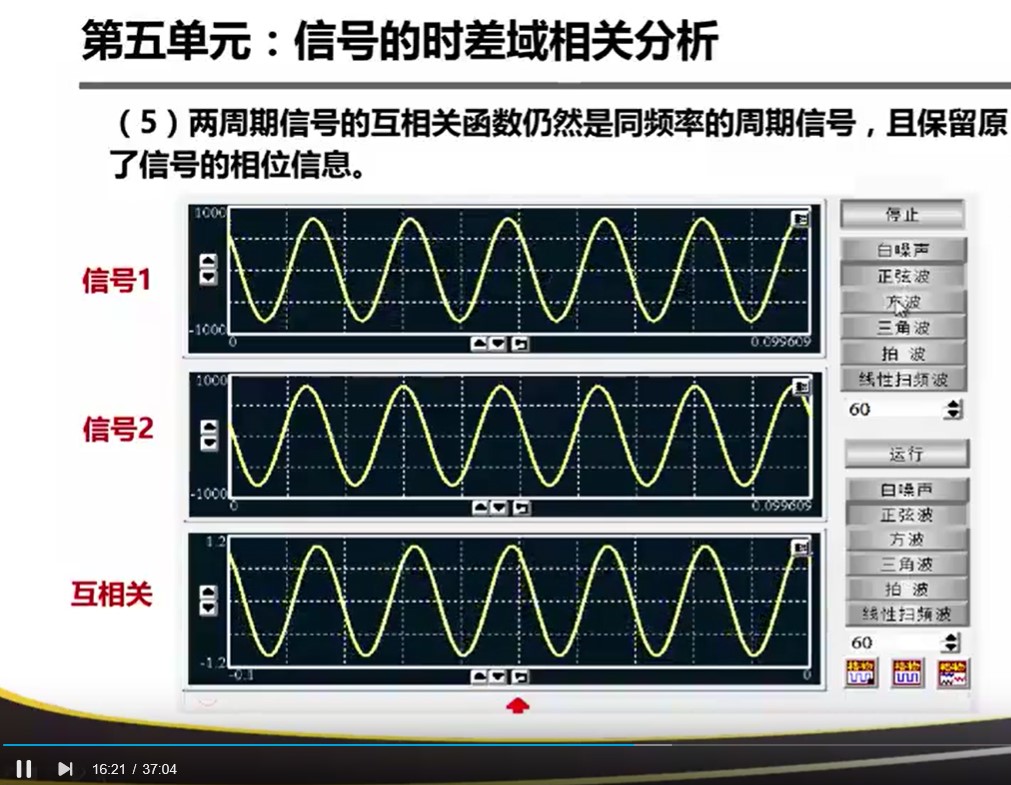
这个互相关的性质对于我来说是最重要的!两个周期信号的互相关函数中包含了相位信息!
12.
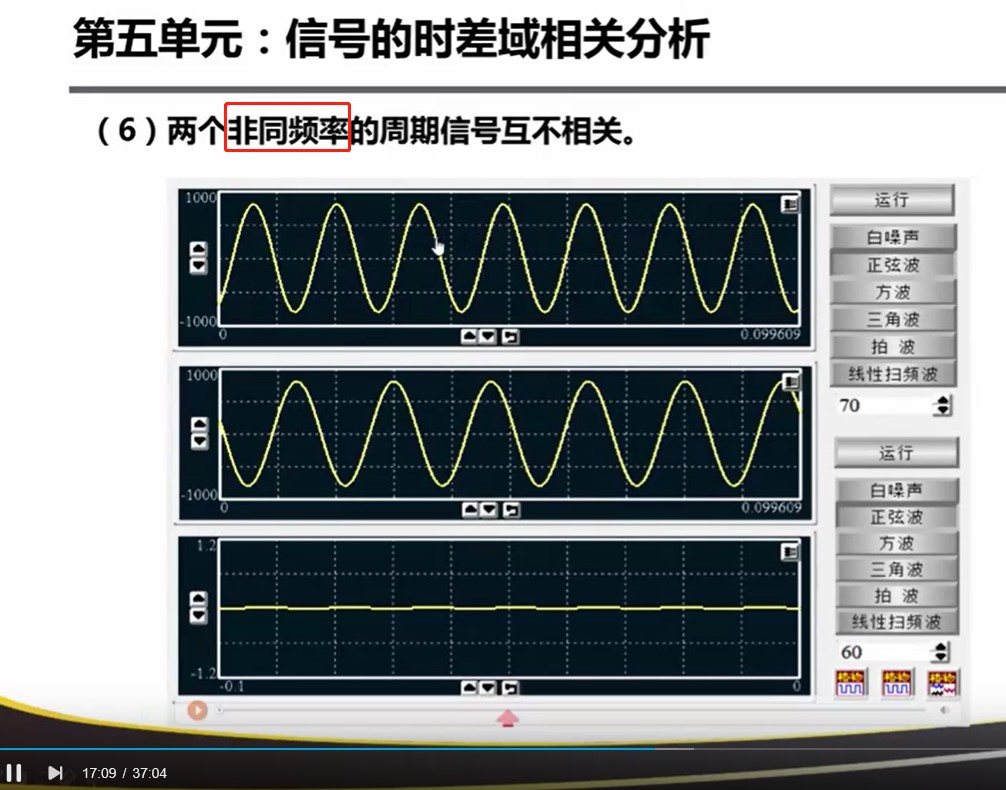
非同频率积分后为0
13.


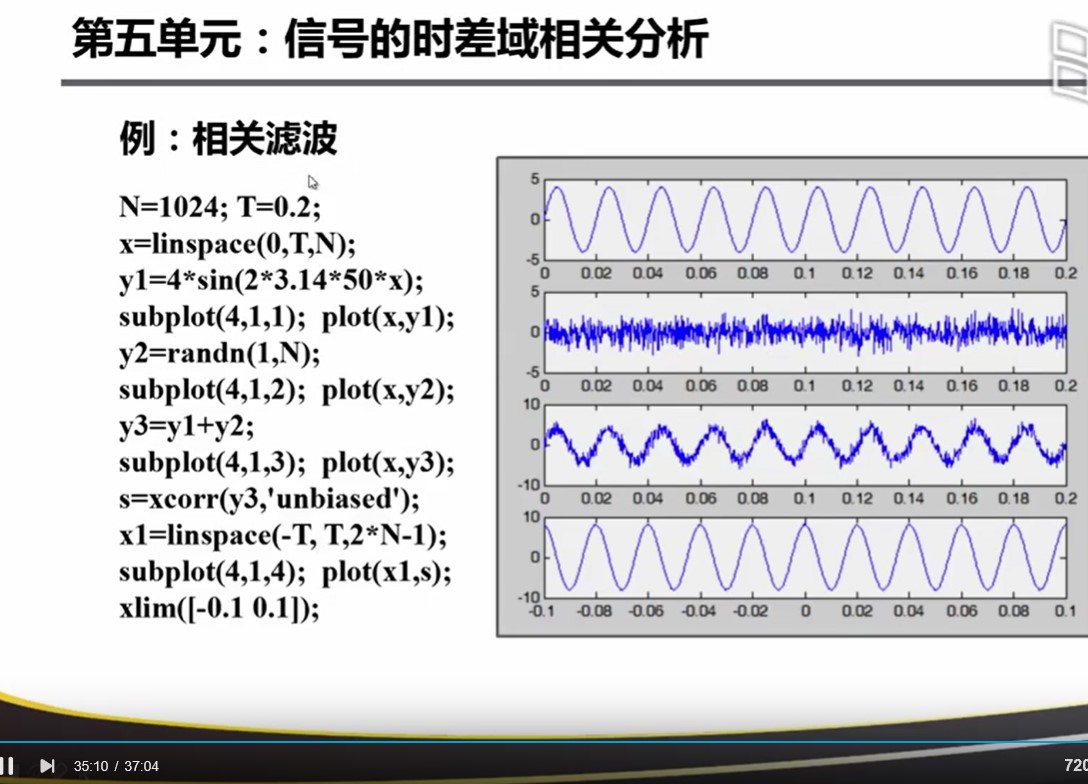
通常来说不会这样计算,而是借用FFT进行一个卷积的运算来实现的!
14.

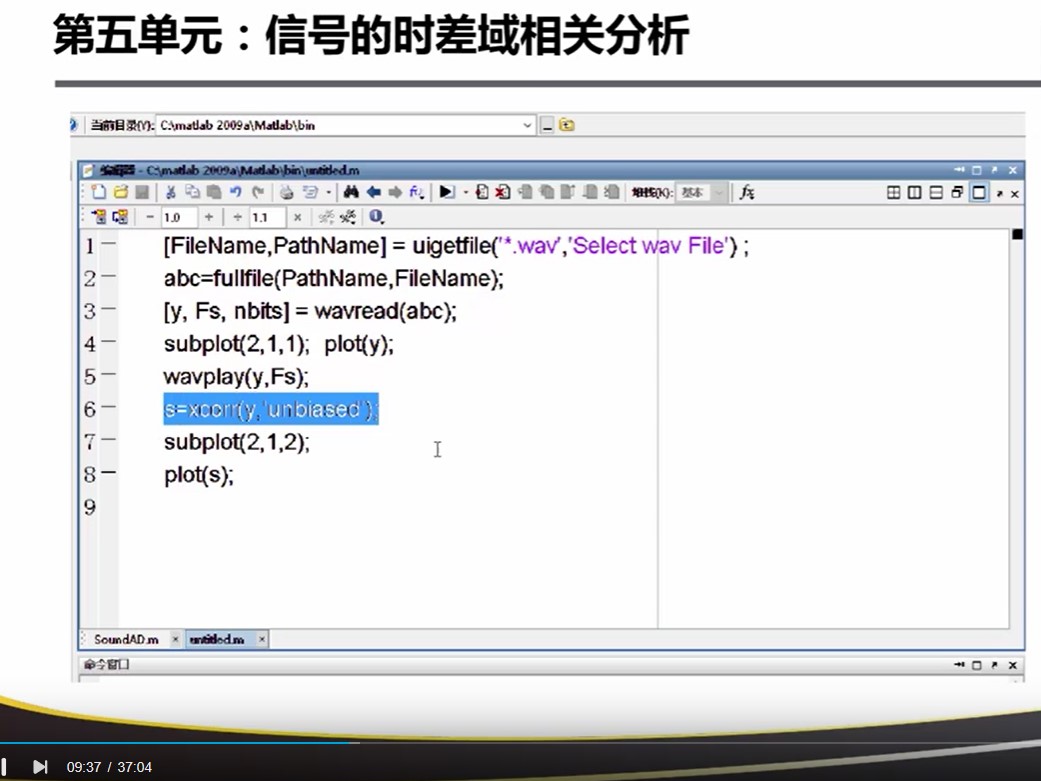
Matlab中的实现。注意在频域中是和 Y(n)的共轭 进行相乘!
15.
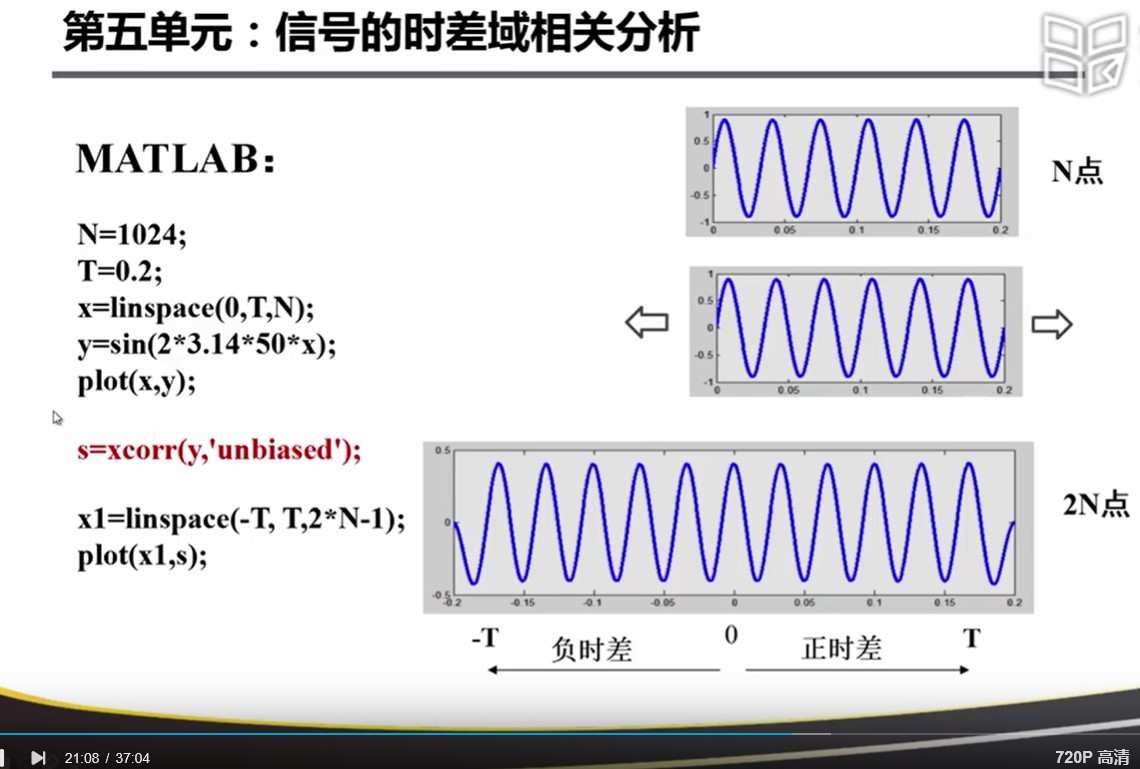
相关系数:长度是2*N个点,一半是正时移。记住加上 unbiased
16.


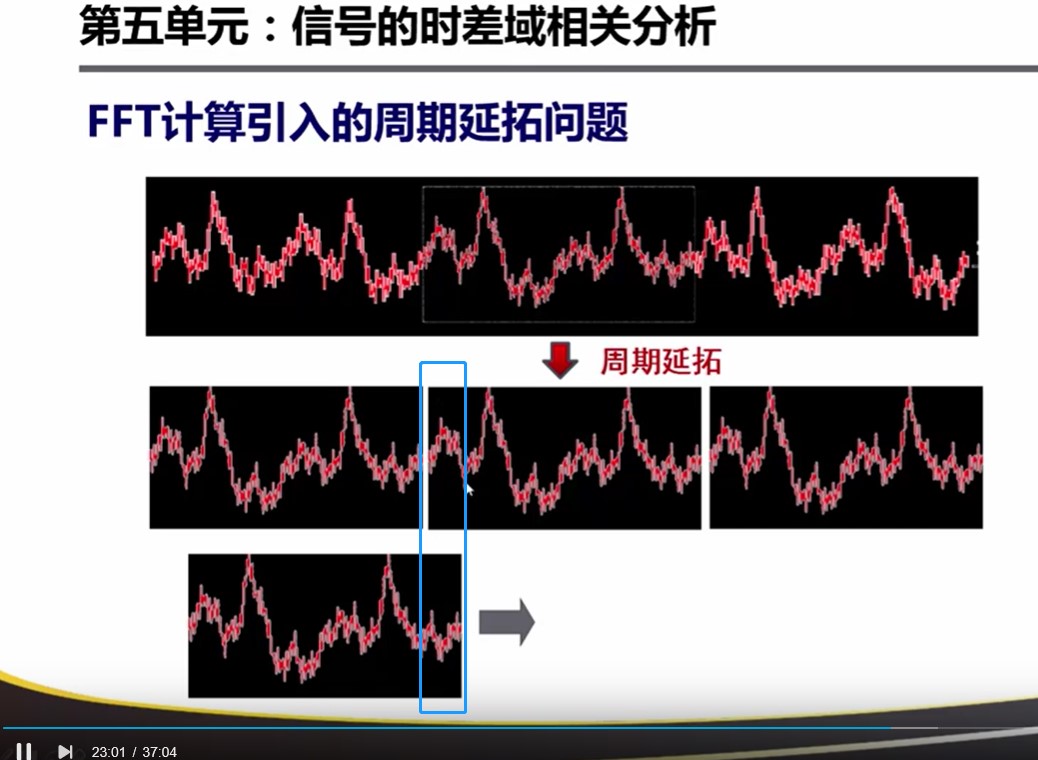
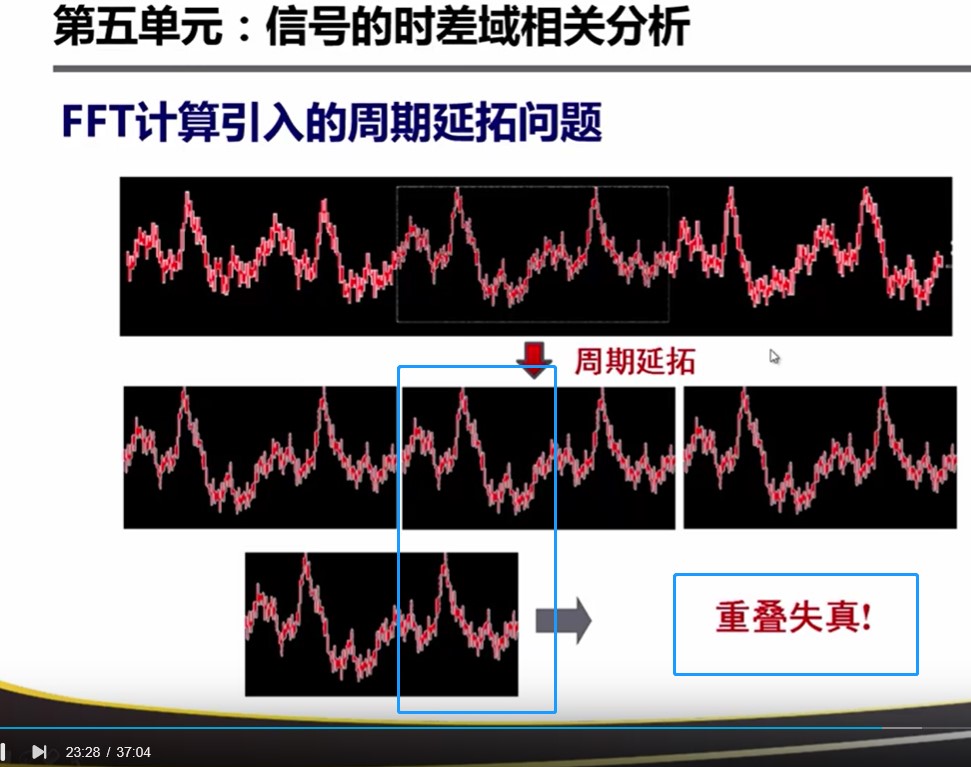
时延τ为0时的值,当时延τ不为0时,会产生重叠失真(因为FFT = 加窗截取+周期延拓)。
17.
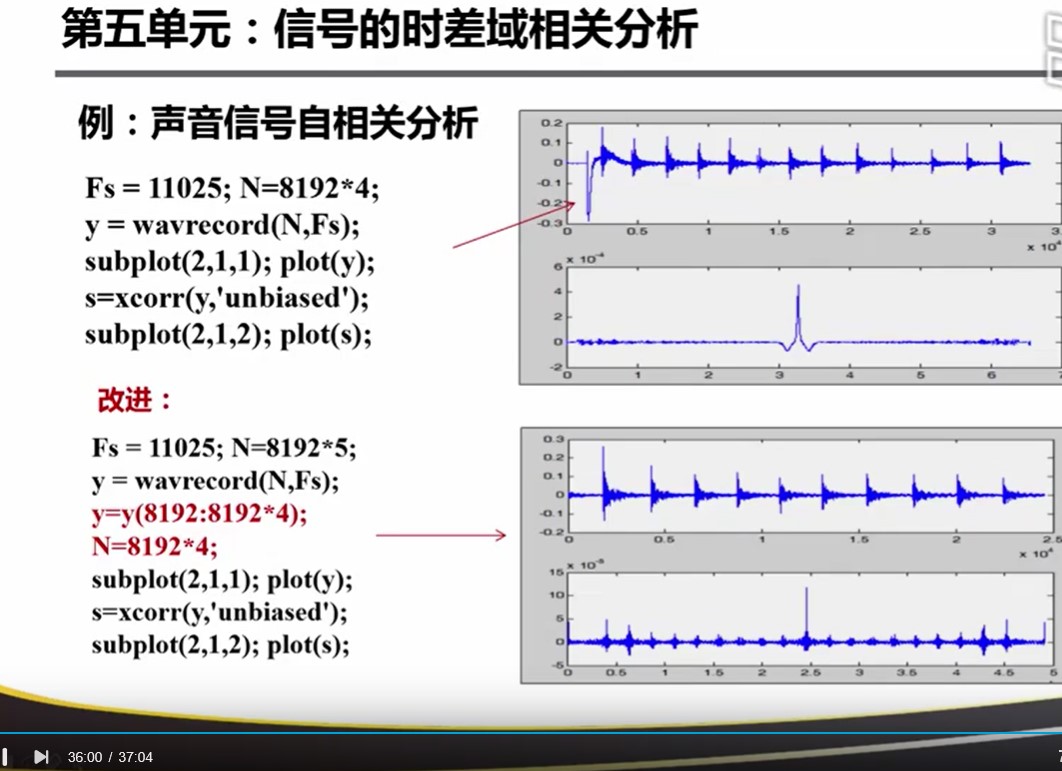
为了避免重叠失真:对FFT的周期延拓做出一定的修改,即:增加和信号长度相等的0点序列。
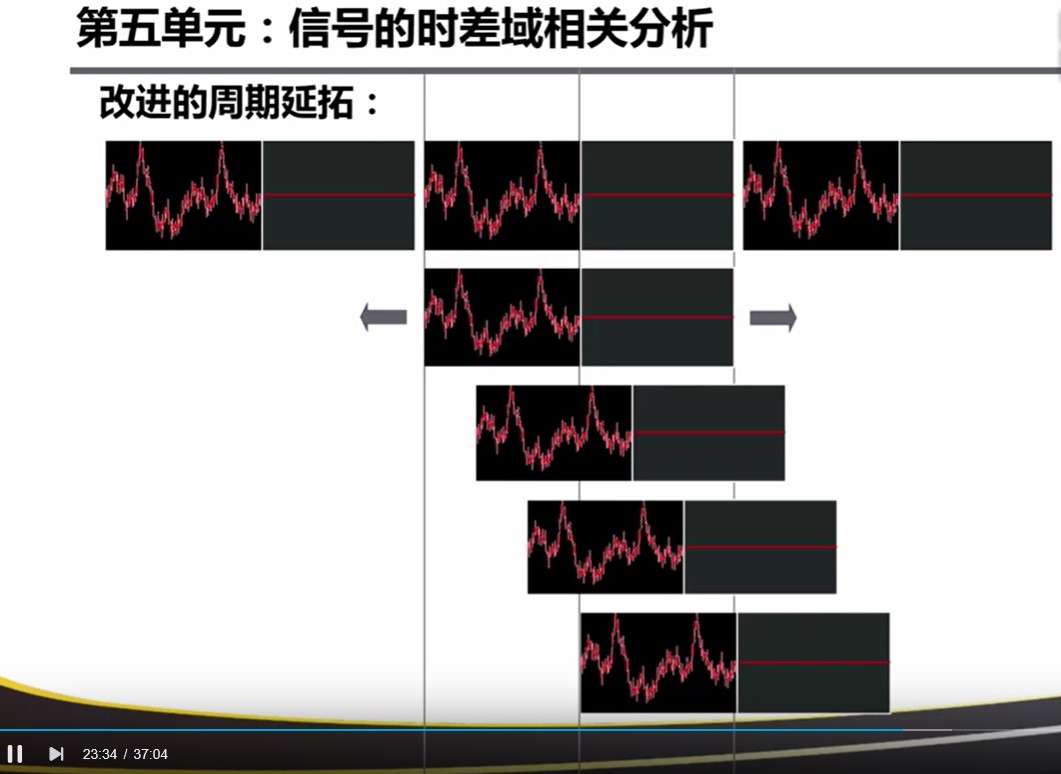
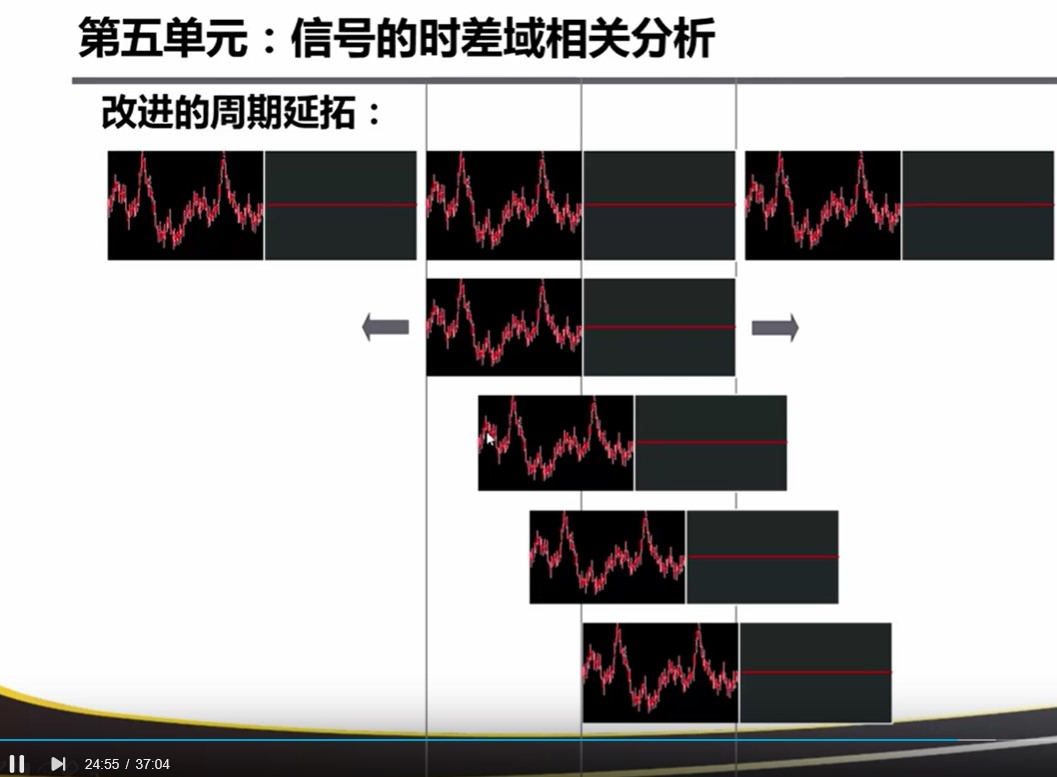
造成的结果是:中心最大,两边逐渐衰减到0。所以导致产生如下图的误差。想要消除这个误差可以加上 unbiased 这个参数
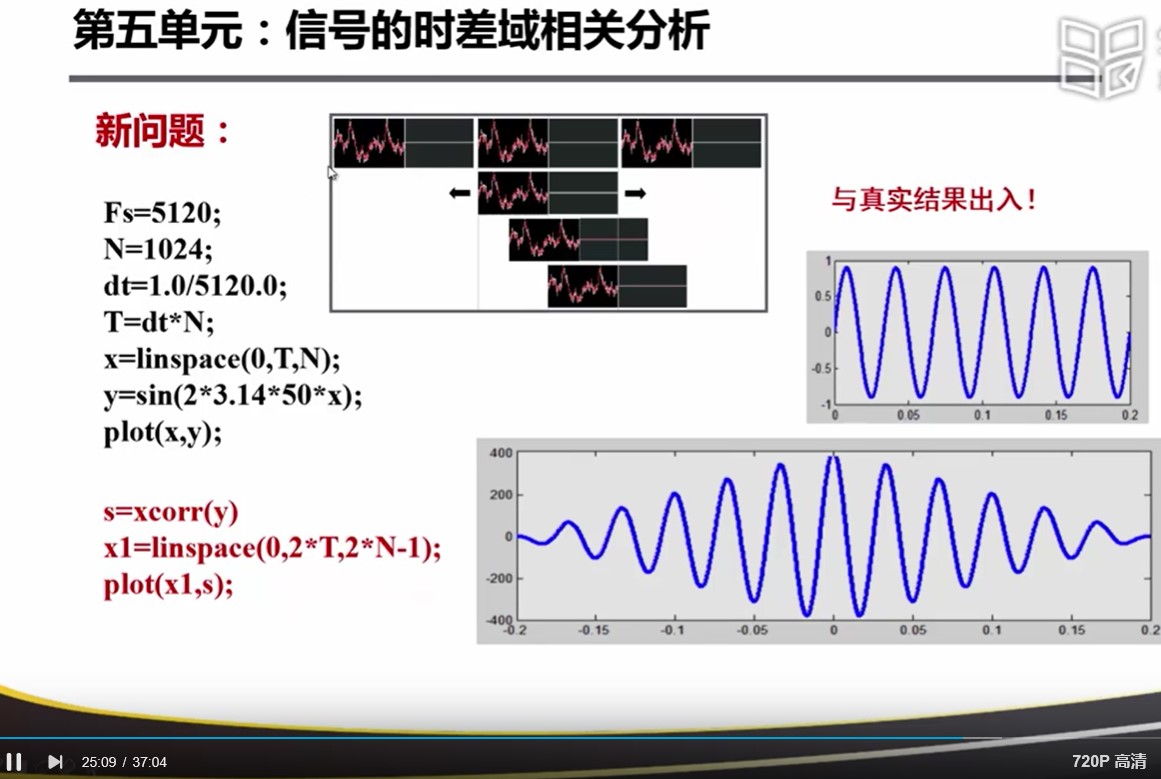
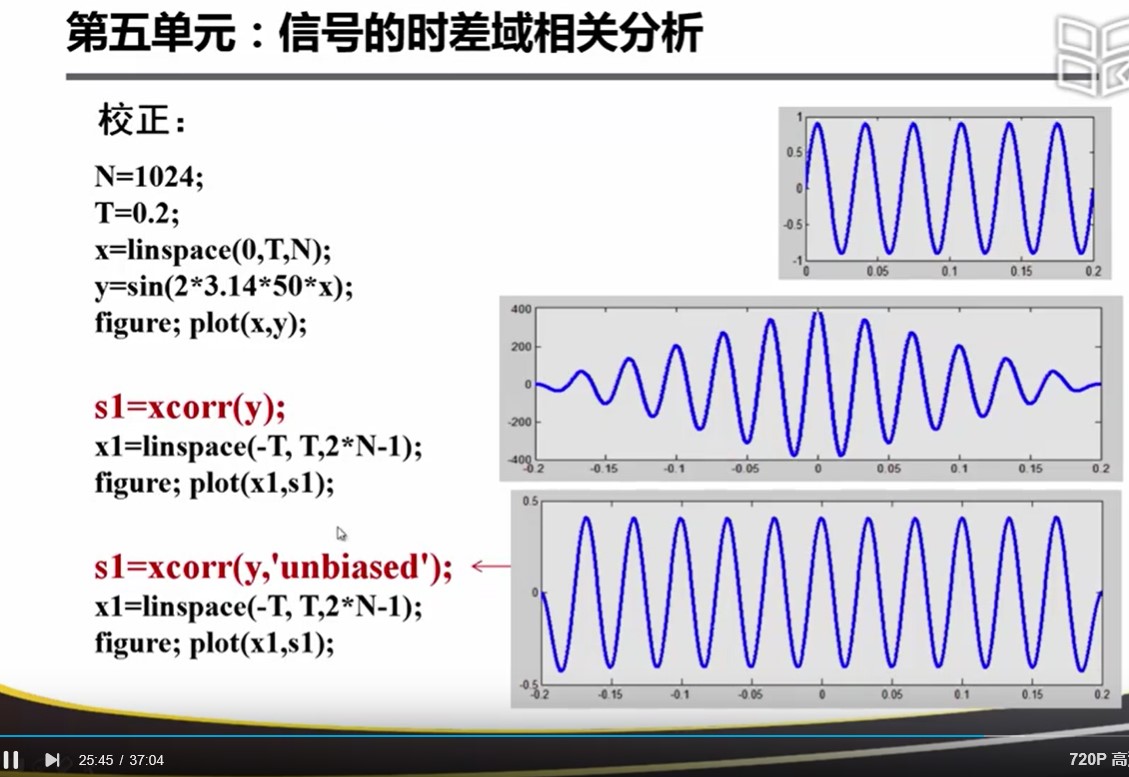
18.
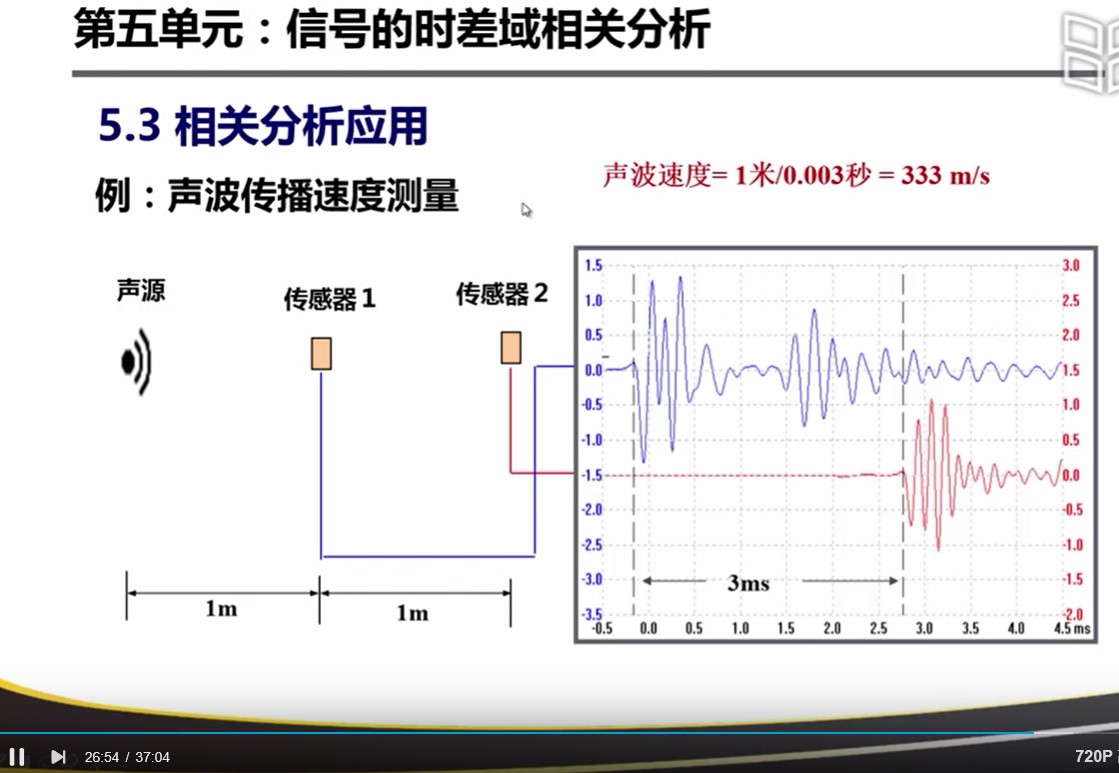
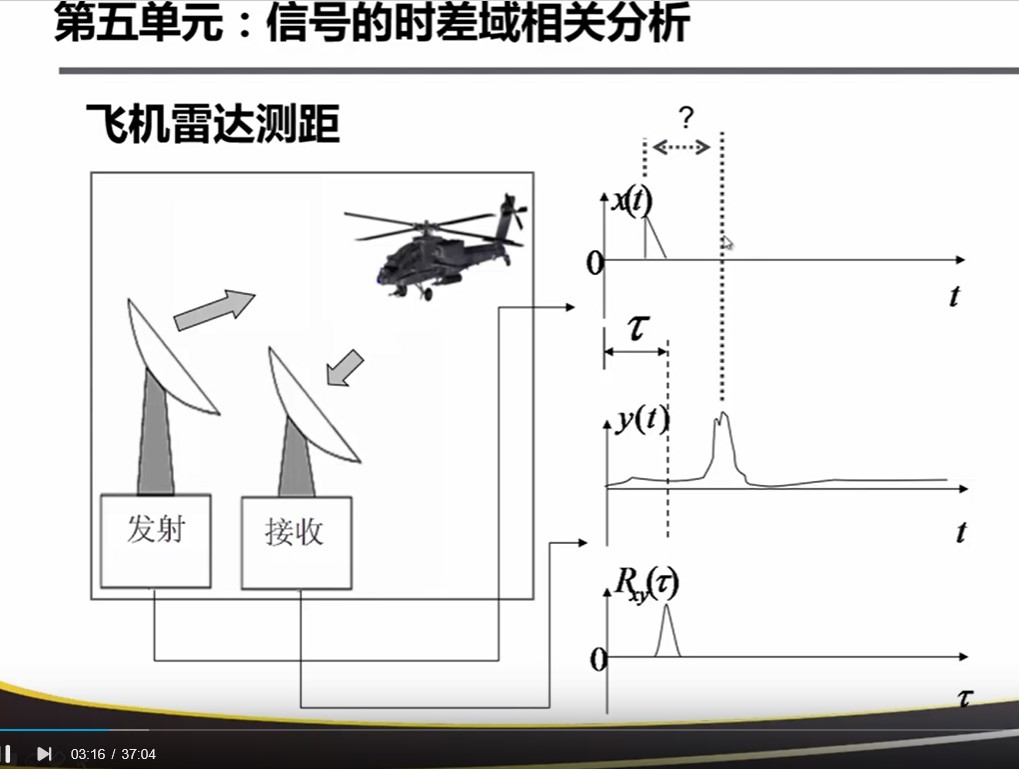
测速
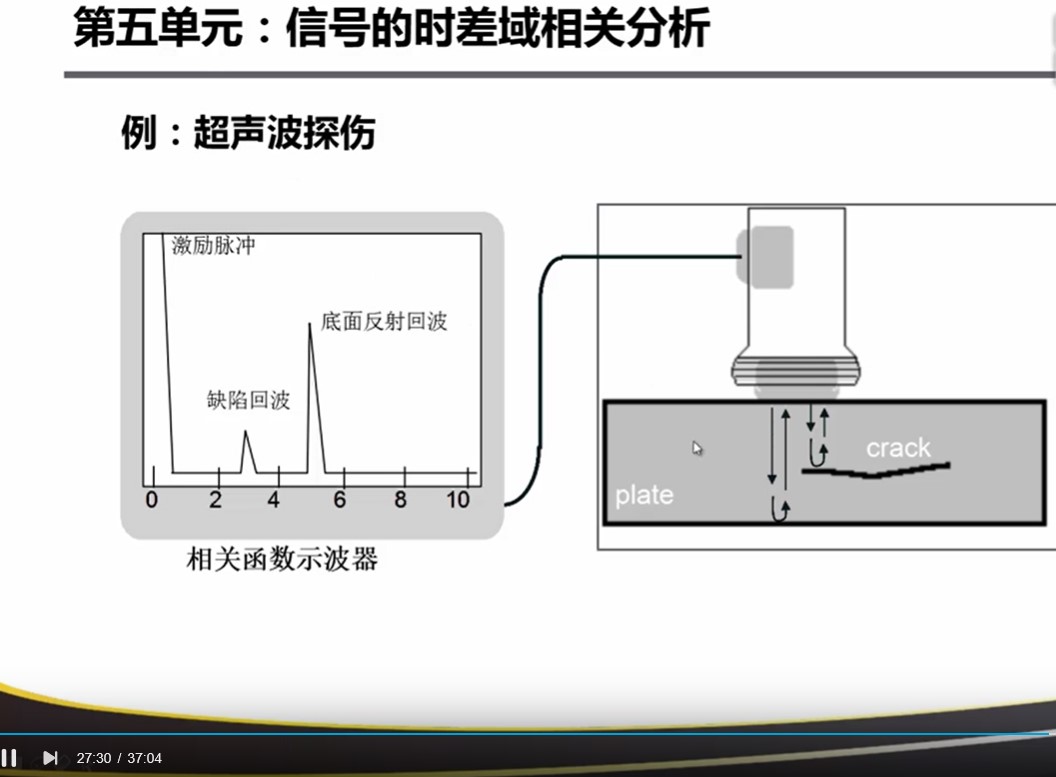
测距
19.
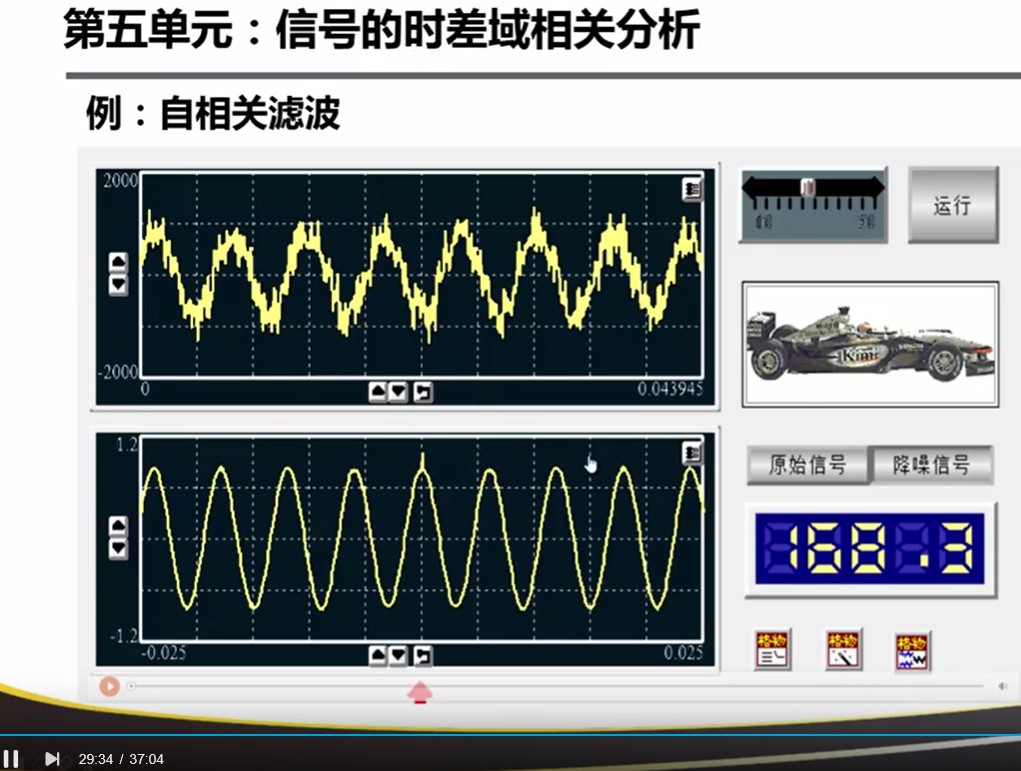
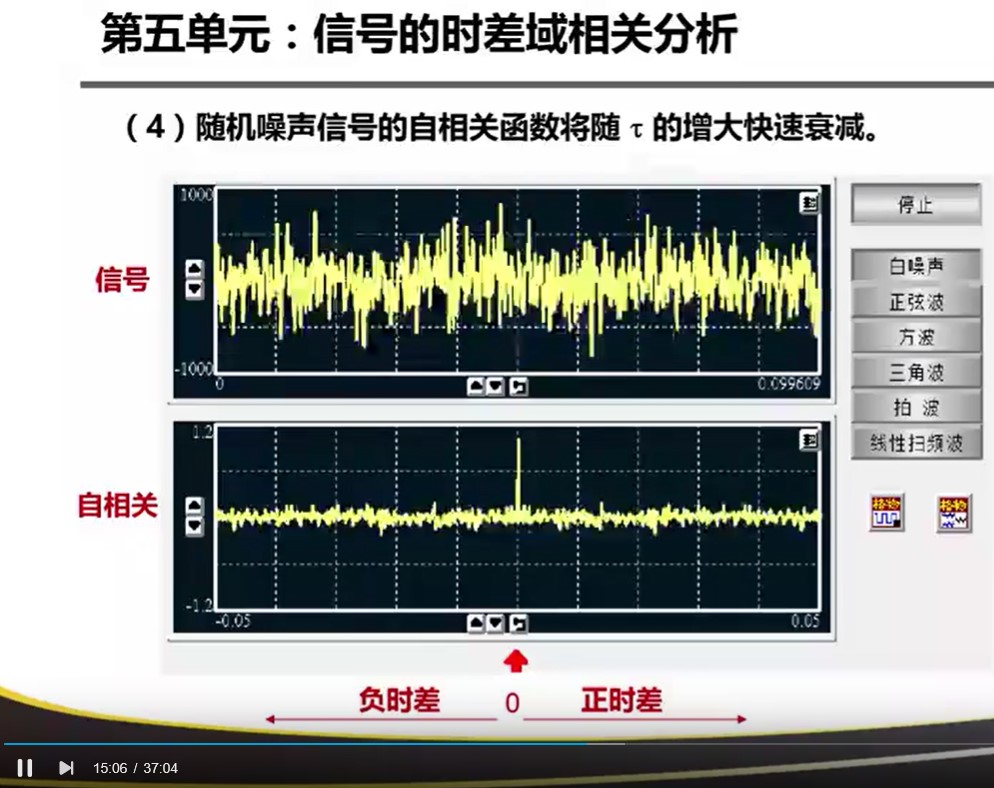
噪声信号做自相关后,只有原点有较大的值,在其他时间部分快速衰减。周期信号做自相关依然是自相关,所以用自相关的方法去测量周期。
20.

21.
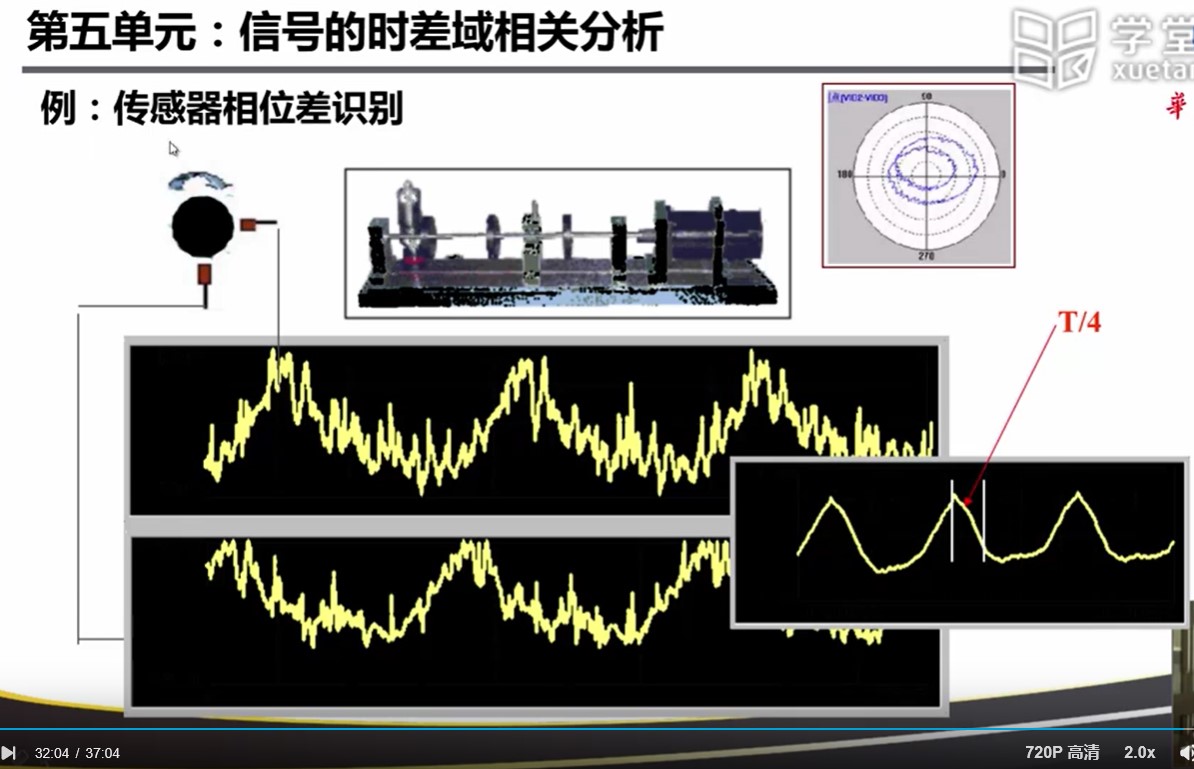
相位检测!
22.