祘头君的字符(DFS)

一、题目

有n名选手在玩游戏，他们每个人有一个字符，每个字符都有自己固定的若干个特征。特征的种类数为k。每个人的特征为特征总集的一个子集。
两个字符的相似度定义为：如果两个字符A和B同时拥有某个特征或者同时没有某个特征，它们的相似度加一。
蒜头君想创造出一个字符，它与其它n名选手的字符的相似度分别为a1, a2, …, an，假设其中最大的相似度为ax，蒜头君希望ax尽量小。

输入格式

输入第一行包含两个整数n，k（1 <= n <= 105, 1 <= k <= 20）分别表示选手的个数以及特征的种类数。下面n行每行包含一个字符串表示某个选手的特征状态，如果在j位置有一个1表示他有第j个特征，否则没有。

输出格式

输出一个满足条件的字符串。
注：本题答案不唯一，符合要求的答案均正确

样例输入1

3 5
01001
11100
10111

样例输出1

00010

样例输入2

1 4
0000

样例输出2

1111

二、分析

（一）定义距离

本题考察相似度，反过来说就是考察不相似度。不相似度大，相似度就小；不相似度小，相似度就大。
可以用距离来衡量不相似度。若两个数有一位不一样，则不相似度为1，即距离为1。若两个数有两位不一样，则不相似度为2，即距离为2。若两个数有三位不一样，则不相似度为3，即距离为3。依此类推。

（二）求最大距离

题目要求最大的相似度最小，也就是求最小的距离最大。现在分析样例1，画出含3棵树的图如下所示：

 

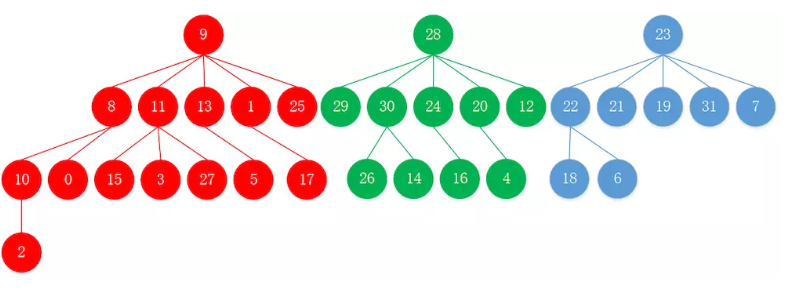
与01001距离为1的结点有01000，01011，01101，00001，11001。换成十进制，即与9距离为1的结点为8，11，13，1，15。
与11100距离为1的结点有11101，11110，11000，10100，01100。换成十进制，即与28距离为1的结点为29，30，24，20，12。
与10111距离为1的结点有10110，10101，10011，11111，00111。换成十进制，即与23距离为1的结点为22，21，19，31，7。
与01000距离为1的节点有01001，01010，01100，00000，11000。换成十进制，即与8距离为1的节点为9，10，12，0，24。这里9即为第一层的节点。12和24与第一棵树的根节点28的距离为1。另两个节点10和 0，与第一层节点9的距离为2。
从图形里可以看出，节点10、节点0与第一层三个根节点的最小距离就是2。因为若把这两个节点放到28那棵树上，则这两个节点与根节点28的距离必然大于或等于2。同样若把这两个节点放到23那棵树上，则这两个节点与根节点23的距离必然大于或等于2。
把2k = 25 = 32个节点都挂到3棵树上后，可以发现节点2与根节点9的距离最大，为3。若把节点2挂到根节点为28的树上，则节点2与根节点28的距离必然大于或等于3（实际上很容易算出节点2与节点28的距离是4）。同样道理，若把节点2挂到根节点为23的树上，则节点2与根节点23的距离必然大于或等于3（实际上很容易算出节点2与节点23的距离是3）。
综上，三棵树上的最小深度（距离）为3，这就是所求的答案。

（三）广度优先搜索

这里需要用到广度优先搜索。广度优先搜索需要用到队列。在每个节点入队时，都要把距离为1的节点入队，入队即说明节点被遍历过。当然，已经遍历过的节点，就不需要再次入队了。在这里，可以根据一个节点的距离大小来判断节点是否已经遍历过。具体可以看实现代码。

三、代码

#include<bits/stdc++.h>
using namespace std;

const int N = 21;
const int MAXN = 1e5 + 5;
int dist[1<<N], n, k;
char s[MAXN];
queue<int> q;

void bfs()
{
    while(q.size())
    {
        int u = q.front();
        q.pop(); // 队首元素出队，接着要把相邻的5个元素入队
        for(int i = 0; i < k; i++)
        {
//            if(i == 0)
//            {
//                printf("
>>>>>>>>>>>>
dist[%d] = %d
", u, dist[u]);
//            }
//            printf("
* dist[%d] = %d
", u ^ (1<<i), dist[u ^ (1<<i)]);
            if(dist[u ^ (1<<i)] > dist[u])
            {
                dist[u ^ (1<<i)] = dist[u] + 1; // 不相似度即距离加1
//                printf("** dist[%d] = %d
", u ^ (1<<i), dist[u ^ (1<<i)]);
                q.push(u^(1<<i));
            }
        }
    }
}

// 十进制化为二进制再打印出来
void PRINT(int val)
{
    for(int i = k - 1; i >= 0; i--)
    {
        printf("%d",(val & (1<<i)) > 0);
    }
}

int main()
{
    freopen("test.in", "r", stdin);
    memset(dist, 0x7f, sizeof(dist));
    scanf("%d%d", &n, &k);
    for(int i = 1; i <= n; i++)
    {
        // 把几个原始的数据按顺序入队
        scanf("%s", s);
        int len = strlen(s), p = 0, sValue = 0;
        for(int j = len-1; j >= 0; j--)
        {
            sValue += (1<<p) * (s[j]-'0');
            p++;
        }
        q.push(sValue);
        dist[sValue] = 0;
    }

    bfs();

    int maxDist = 0, ans = 0;
    for(int i = 0; i < (1<<k); i++)
    {
        if(dist[i] > maxDist)
        {
            maxDist = dist[i];
            ans = i;
        }
    }

    PRINT(ans);

    return 0;
}