self-taught learning 在特征提取方面完全是用的无监督的方法,对于有标记的数据,可以结合有监督学习来对上述方法得到的参数进行微调,从而得到一个更加准确的参数a。
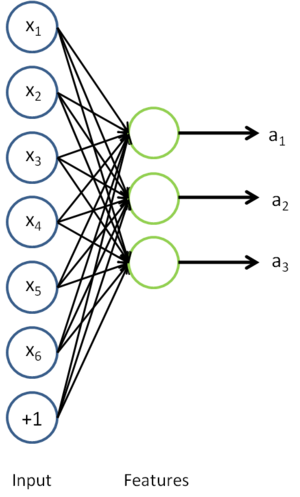
在self-taught learning中,首先用 无标记数据训练一个sparse autoencoder,这样用对于原始输入x,经过sparse autoencoder得到隐层特征a:
这样对于分类问题,目标是预测样本的类别标号  。现在的标注数据集
。现在的标注数据集 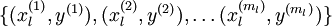 ,包含
,包含 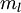 个标注样本。此前已经说明,可以利用稀疏自编码器获得的特征
个标注样本。此前已经说明,可以利用稀疏自编码器获得的特征 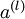 来替代原始特征。这样就可获得训练数据集
来替代原始特征。这样就可获得训练数据集 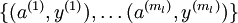 。最终,训练出一个从特征
。最终,训练出一个从特征 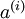 到类标号
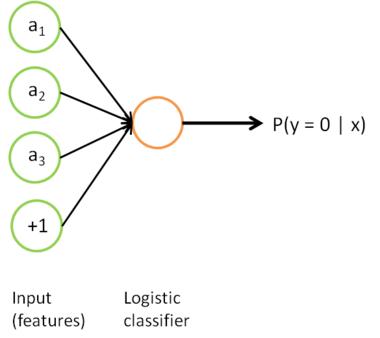
到类标号 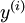 的 logistic 分类器。为说明这一过程,用下图描述 logistic 回归单元(橘黄色)。
的 logistic 分类器。为说明这一过程,用下图描述 logistic 回归单元(橘黄色)。
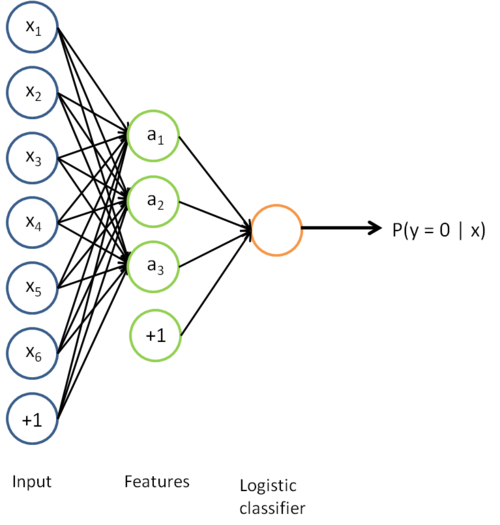
把上述两个步骤结合结合起来,便得到:
该模型的参数通过两个步骤训练获得:在该网络的第一层,将输入  映射至隐藏单元激活量
映射至隐藏单元激活量 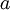 的权值
的权值 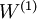 可以通过稀疏自编码器训练过程获得。在第二层,将隐藏单元
可以通过稀疏自编码器训练过程获得。在第二层,将隐藏单元 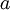 映射至输出
映射至输出  的权值
的权值 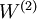 可以通过 logistic 回归或 softmax 回归训练获得。
可以通过 logistic 回归或 softmax 回归训练获得。
这个最终分类器整体上显然是一个大的神经网络。因此,在训练获得模型最初参数(利用自动编码器训练第一层,利用 logistic/softmax 回归训练第二层)之后,我们可以进一步修正模型参数,进而降低训练误差。具体来说,我们可以对参数进行微调(fun-tuning),在现有参数的基础上采用梯度下降或者 L-BFGS 来降低已标注样本集 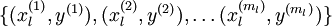 上的训练误差。
上的训练误差。
使用微调时,初始的非监督特征学习步骤(也就是自动编码器和logistic分类器训练)有时候被称为预训练。微调的作用在于,已标注数据集也可以用来修正权值 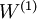 ,这样可以对隐藏单元所提取的特征
,这样可以对隐藏单元所提取的特征 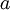 做进一步调整。
做进一步调整。
需要注意的是:通常仅在有大量已标注训练数据的情况下使用微调。在这样的情况下,微调能显著提升分类器性能。然而,如果有大量未标注数据集(用于非监督特征学习/预训练),却只有相对较少的已标注训练集,微调的作用非常有限。
之前所提到的network一般是三层,下面讲逐渐考虑多层的网络,通过加深网络层数,我们可以计算更多复杂的输入特征。因为每一个隐藏层可以对上一层的输出进行非线性变换,因此深度神经网络拥有比“浅层”网络更加优异的表达能力(例如可以学习到更加复杂的函数关系)。
注意神经网络应该使用非线性的激活函数,因为线性激活函数的表达能力有限,多层线性函数的组合得到的仍然是线性的表达能力,因此激活函数是线性情况下,加深网络层数然并卵,并不会增加表达能力。
加深网络的优点:
一、网络每加深一层得到的表达能力将是之前的指数倍,比如说用k层神经网络能学习到的函数(且每层网络节点个数时多项式的)如果要用k-1层神经网络来学习,则这k-1层神经网络节点的个数必须是k的指数倍的庞大数字。
二、不同层的网络学习到的特征是由最底层到最高层慢慢上升的。比如在图像的学习中,第一个隐含层层网络可能学习的是边缘特征,第二隐含层就学习到的是轮廓,后面的就会更高级有可能是图像目标中的一个部位,也就是是底层隐含层学习底层特征,高层隐含层学习高层特征。
之前研究者们主要使用的学习算法是:随机初始化深度网络的权重,然后使用有监督的目标函数在有标签的训练集 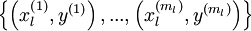 上进行训练。
上进行训练。
这样有一些缺点:
一、数据获取问题,使用上面提到的方法,我们需要依赖于有标签的数据才能进行训练。然而有标签的数据通常是稀缺的,因此对于许多问题,我们很难获得足够多的样本来拟合一个复杂模型的参数。例如,考虑到深度网络具有强大的表达能力,在不充足的数据上进行训练将会导致过拟合
二、使用监督学习方法来对浅层网络(只有一个隐藏层)进行训练通常能够使参数收敛到合理的范围内。但是当用这种方法来训练深度网络的时候,并不能取得很好的效果。比如使用监督学习方法训练神经网络时,通常会涉及到求解一个高度非凸的优化问题(例如最小化训练误差 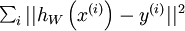 ,其中参数
,其中参数 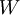 是要优化的参数。对深度网络而言,这种非凸优化问题的搜索区域中充斥着大量“坏”的局部极值,因而使用梯度下降法(或者像共轭梯度下降法,L-BFGS等方法)效果并不好。
是要优化的参数。对深度网络而言,这种非凸优化问题的搜索区域中充斥着大量“坏”的局部极值,因而使用梯度下降法(或者像共轭梯度下降法,L-BFGS等方法)效果并不好。
三、梯度扩散(gradient diffuse),梯度下降法(以及相关的L-BFGS算法等)在使用随机初始化权重的深度网络上效果不好的技术原因是:梯度会变得非常小,当使用反向传播方法计算导数的时候,随着网络的深度的增加,反向传播的梯度(从输出层到网络的最初几层)的幅度值会急剧地减小。结果就造成了整体的损失函数相对于最初几层的权重的导数非常小。这样,当使用梯度下降法的时候,最初几层的权重变化非常缓慢,以至于它们不能够从样本中进行有效的学习。这种问题通常被称为“gradient diffuse”.
梯度扩散导致的问题是:当神经网络中的最后几层含有足够数量神经元的时候,可能单独这几层就足以对有标签数据进行建模,而不用最初几层的帮助。因此,对所有层都使用随机初始化的方法训练得到的整个网络的性能将会与训练得到的浅层网络(仅由深度网络的最后几层组成的浅层网络)的性能相似。
最后补充下,现在随着深度学习的发展,pre-training 变得不再那么重要,因为学者们发现只要数据量足够多,最后深度学习都能给出一个较优的解,并且一些非全连接网络比如LSTM或者CNN等也很难进行pre-training。