题目背景
这是个非常经典的主席树入门题——静态区间第K小
数据已经过加强,请使用主席树。同时请注意常数优化
题目描述
如题,给定N个整数构成的序列,将对于指定的闭区间查询其区间内的第K小值。
输入输出格式
输入格式:
第一行包含两个正整数N、M,分别表示序列的长度和查询的个数。
第二行包含N个整数,表示这个序列各项的数字。
接下来M行每行包含三个整数l, r, kl,r,k , 表示查询区间[l, r][l,r]内的第k小值。
输出格式:
输出包含k行,每行1个整数,依次表示每一次查询的结果
输入输出样例
输入样例#1: 复制
5 5 25957 6405 15770 26287 26465 2 2 1 3 4 1 4 5 1 1 2 2 4 4 1
输出样例#1: 复制
6405 15770 26287 25957 26287
题面非常清晰,区间第k大。首先,每次排序再还原肯定是要跪的。
这时主席树就出现了。
主席树,倒不如说是榕树(有多个根节点,但是却不是森林)。可以说是在用空间换时间。
其实这题,主席树的主体应该是一棵权值线段树。
别人都说主席树是在每个位置维护了一颗线段树,我一直以为是每一个叶节点,其实是在每一个...好吧就是叶节点。
这里可能要把历史值那一题拿出来讲讲,主席树的每一次修改只修改一条链,而不是整个换血,所以为我们的查询提供了方便。
模拟一发:
7 1
1 5 2 6 3 7 4
建树:(感谢@bestFy的数据和图!)


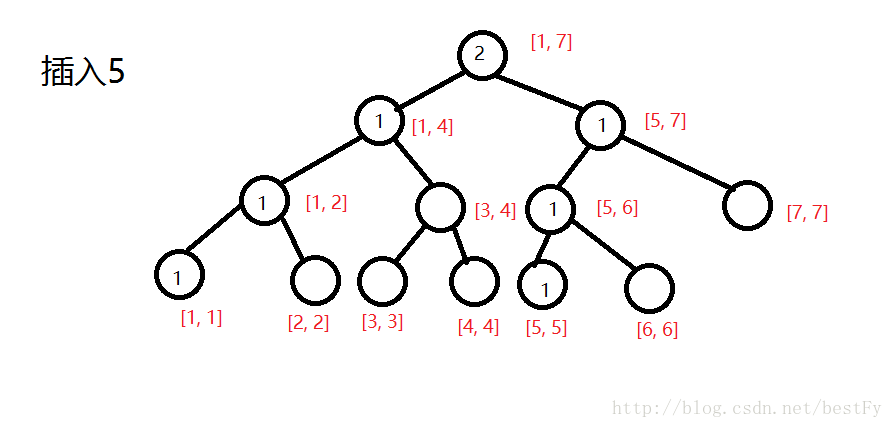
插完所有的之后:

(妥妥的权值线段树)
最终图只是最后一棵线段树的样子,之前的各个线段树依旧在保存着。
于是就出现了旧节点和新建的节点公用一个根节点的情况。于是就可以愉快地进行差分了(因为两个新旧节点是等价的啊)
∴两棵线段树的对应节点相减就是对应区间有的数字啦
所以对于一个区间[l, r],我们可以每次算出在[l, mid]范围内的数,如果数量>=k(k就是第k大),就往左子树走,否则就往右子树走。
于是区间第k大就完成了。
贴代码:
#include<bits/stdc++.h>
变量解释:sum:节点的总数
rt:新旧树的根节点
ls:左儿子
rs:右儿子
tot:当前节点编号 using namespace std; const int maxn=200000; int n,m,tot,sum[maxn<<5],rt[maxn<<5],ls[maxn<<5],rs[maxn<<5],a[maxn],b[maxn],len; int build(int l,int r) { int root=++tot;//每新建一个节点(根) if(l==r) return root;//如果到叶节点了返回根的值,我们要记录下来 int mid=l+r>>1;//二分区间 ls[root]=build(l,mid);//记录下一层的根,也就是左儿子 rs[root]=build(mid+1,r);//同上 return root;//返回大根 } int updata(int l,int r,int root,int k) { int newroot=++tot;//新建的根的编号 ls[newroot]=ls[root];//记录 rs[newroot]=rs[root];//建一个等价的节点,左右儿子也是旧根节点的左右儿子 sum[newroot]=sum[root]+1;//每新建一条链增加一个有值的点,所以+1(权值线段树) if(l==r) return newroot; int mid=l+r>>1; if(k<=mid) ls[newroot]=updata(l,mid,ls[newroot],k);// else rs[newroot]=updata(mid+1,r,rs[newroot],k); return newroot; } int query(int fl,int fr,int l,int r,int k) { int mid=l+r>>1,x=sum[ls[fr]]-sum[ls[fl]];//查询区间里的东西,先遍历左儿子,不行再往右跑 if(l==r) return l; else if(k<=x) return query(ls[fl],ls[fr],l,mid,k);//差分了 else return query(rs[fl],rs[fr],mid+1,r,k-x);//差分了 } int main() { int i,x,l,r,k; scanf("%d%d",&n,&m); for(i=1;i<=n;i++) { scanf("%d",&a[i]); b[i]=a[i]; } sort(b+1,b+1+n); len=unique(b+1,b+1+n)-b-1;//去重,神仙操作 //printf("%d ",len); rt[0]=build(1,len);//根的“tot”(下标,第几个点) for(i=1;i<=n;i++)//要对每一个节点建树,所以n次加边 { x=lower_bound(b+1,b+1+len,a[i])-b;//离散化,更新相对大小,也就是把所有数的编号弄小 rt[i]=updata(1,len,rt[i-1],x);//新根的编号 } for(i=1;i<=m;i++) { scanf("%d%d%d",&l,&r,&k); printf("%d ",b[query(rt[l-1],rt[r],1,len,k)]);//query返回的是下标,所以要这么长一串。。 } for(int i=0;i<=3*n;i++) { //if(sum[i]==0)break; printf("%d ",sum[i]); } return 0; }
(完)