st表,一种高效的区间最值查询(RMQ)算法。本质其实是一个动态规划。
其实吧,对于看过线性dp的人来说应该不难理解,只是处理有些麻烦。但是本土狗因为-1的问题居然改了许久...
用两个2^i的区间把整个区段覆盖,dp[i][j]表示区间最值,从i开始,向前2^j个数字。根据动态规划的定义,把这个区间分割成两个小区间,于是就有
dp[i][j]=max(dp[i][j-1],dp[i][i+(1<<j-1)]);(然而我在这里处理区间的时候多减了一个1....)
一直分割下去,直到1。复杂度O(nlogn)。
于是查询:
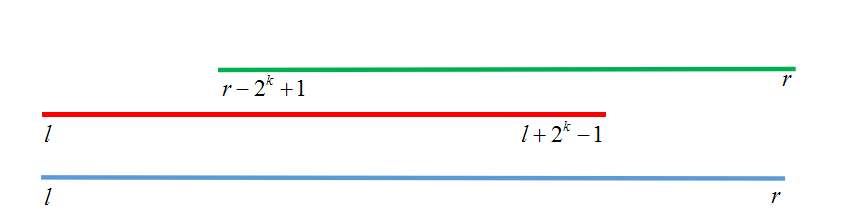
我们找到左右区间大小(y-x+1),把它log一下,再2的次方一下,就成了覆盖区间的最大2^i次方的区间。同理,右区间也是。比较两区间最值,就可以得出最值了。
code:
#include<iostream> #include<cstdio> using namespace std; const int maxn=100005; int n,m,a[maxn],dp[maxn][25],l[maxn]; int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); } l[0]=-1; for(int i=1;i<=n;++i) { dp[i][0]=a[i]; l[i]=l[i>>1]+1; } for(int j=1;j<=25;++j) { for(int i=1;i+(1<<j)-1<=n;++i) { dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]); } } for(int i=1;i<=m;i++) { int x,y; scanf("%d%d",&x,&y); int s=l[y-x+1]; printf("%d ",max(dp[x][s],dp[y-(1<<s)+1][s])); } return 0; }
类比线段树:
优点:
1、码量小
2、快(不用说了,线段树常数大得呦...)
缺点:
1、只能静态
2、只能最值
(完)