BZOJ1269
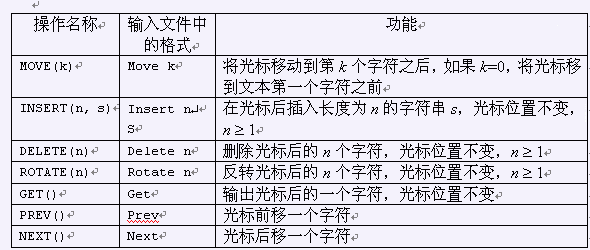
上一篇文章介绍了Rope的简单应用,这里多了一个操作,区间翻转
同时维护一正一反两个rope……反转即交换两个子串
下面给出代码:
1 #include<cstdio> 2 #include<ext/rope> 3 using namespace std; 4 using namespace __gnu_cxx; 5 inline int read() 6 { 7 int x=0;char ch=getchar(); 8 while(ch>'9'||ch<'0') ch=getchar(); 9 while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} 10 return x; 11 } 12 int n,cur,len; 13 rope<char> a,b,tmp; 14 char s[2000005],rs[2000005]; 15 int main() 16 { 17 n=read(); 18 int x; 19 while(n--) 20 { 21 scanf("%s",s); 22 switch(s[0]) 23 { 24 case 'M':cur=read();break; 25 case 'P':cur--;break; 26 case 'N':cur++;break; 27 case 'G':printf("%c ",a[cur]);break; 28 case 'I': 29 x=read();len=a.length(); 30 for(int i=0;i<x;i++) 31 { 32 s[i]=getchar(); 33 while(s[i]==' ') s[i]=getchar(); 34 rs[x-i-1]=s[i]; 35 } 36 rs[x]=s[x]=0; 37 a.insert(cur,s); 38 b.insert(len-cur,rs); 39 break; 40 case 'D': 41 x=read();len=a.length(); 42 a.erase(cur,x); 43 b.erase(len-cur-x,x); 44 break; 45 case 'R': 46 x=read();len=a.length(); 47 tmp=a.substr(cur,x); 48 a=a.substr(0,cur)+b.substr(len-cur-x,x)+a.substr(cur+x,len-cur-x); 49 b=b.substr(0,len-cur-x)+tmp+b.substr(len-cur,cur); 50 break; 51 } 52 } 53 return 0; 54 }
Rope被称为可持久化平衡树,是因为它可以:
rope<char>*a,*b; a=new rope<char>; b=new rope<char>(*a);
或者
his[i]=new rope<char>(*his[i-1]);
也就是O(1)拷贝历史版本的平衡树,很完美的一个可持久化平衡树但是呢,数值操作不支持
我也不知道底层是用块状链表实现的还是用平衡树实现的,复杂度到底是根号还是对数不好说