这里给出一个例题BZOJ1857,题意是这样的:
在一个2维平面上有两条传送带,每一条传送带可以看成是一条线段。两条传送带分别为线段AB和线段CD。
lxhgww在AB上的移动速度为P,在CD上的移动速度为Q,在平面上的移动速度R。
现在lxhgww想从A点走到D点,他想知道最少需要走多长时间
根据肯定知道最终的路径是一个这样形状的
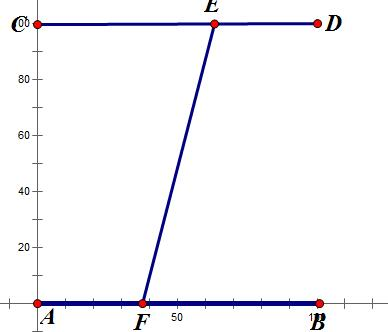
关键就在于确定E和F点的位置
确定的时候控制变量,定E求F,定F求E
假设我们是定E求F,那么在AB上肯定存在一个点满足AF+FE最小
在这个最值点的左右两侧都不能得到最优的结果
如果把这个距离值反馈成函数那么它就是一个单峰函数
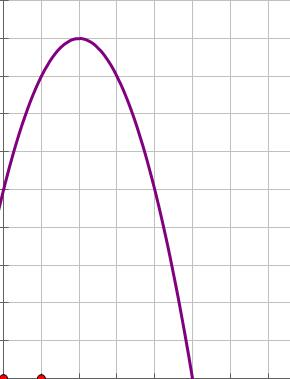
然后我们只要求这个机制就好了,方法就是三分法,下面给出介绍:
对于任意一个上凸函数,选取函数上任意两个点A,B(xA<xB),若满足yA<yB,那么该函数的极值点必然在[xA,+∞)中,若满足yA>yB,那么该函数极值点必然在(-∞,xB]中,若满足yA=yB,那么该函数的极值点必然在[xA,xB]中。
对于任意一个下凸函数,选取函数上任意两个点A,B(xA<xB),若满足yA<yB,那么该函数的极值点必然在(-∞,xB]中,若满足yA>yB,那么该函数极值点必然在[xA,+∞)中,若满足yA=yB,那么该函数的极值点必然在[xA,xB]中。
然后用这个写程序就好了。
1 #include<cstdio> 2 #include<cmath> 3 #define eps 1e-3 4 int ax,ay,bx,by; 5 int cx,cy,dx,dy; 6 int p,q,r; 7 inline int read() 8 { 9 int x=0,f=1;char ch=getchar(); 10 while(ch<'0'||ch>'9') {if(ch=='-')f=-1;ch=getchar();} 11 while(ch>='0'&&ch<='9') {x=x*10+ch-'0';ch=getchar();} 12 return x*f; 13 } 14 double dis(double x1,double y1,double x2,double y2) 15 { 16 return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); 17 } 18 double cal(double x,double y) //x和y是计算完的AB上的点 19 { 20 double lx=cx,ly=cy,rx=dx,ry=dy; 21 double x1,y1,x2,y2,t1,t2; 22 while(fabs(rx-lx)>eps||fabs(ry-ly)>eps) 23 { 24 x1=lx+(rx-lx)/3;y1=ly+(ry-ly)/3; 25 x2=lx+(rx-lx)/3*2;y2=ly+(ry-ly)/3*2; 26 t1=dis(ax,ay,x,y)/p+dis(x,y,x1,y1)/r+dis(x1,y1,dx,dy)/q; 27 t2=dis(ax,ay,x,y)/p+dis(x,y,x2,y2)/r+dis(x2,y2,dx,dy)/q; 28 if(t1>t2){lx=x1;ly=y1;} 29 else {rx=x2;ry=y2;} 30 } 31 //计算完lx和ly是CD上的点 32 return dis(ax,ay,x,y)/p+dis(x,y,lx,ly)/r+dis(lx,ly,dx,dy)/q; 33 } 34 int main() 35 { 36 ax=read(),ay=read(),bx=read(),by=read(); 37 cx=read(),cy=read(),dx=read(),dy=read(); 38 p=read(),q=read(),r=read(); 39 40 double lx=ax,ly=ay,rx=bx,ry=by; 41 double x1,y1,x2,y2,t1,t2; 42 while(fabs(rx-lx)>eps||fabs(ry-ly)>eps) 43 { 44 x1=lx+(rx-lx)/3;y1=ly+(ry-ly)/3; 45 x2=lx+(rx-lx)/3*2;y2=ly+(ry-ly)/3*2; 46 t1=cal(x1,y1);t2=cal(x2,y2); //用CD结果迭代算AB 47 if(t1>t2) {lx=x1;ly=y1;} 48 else {rx=x2;ry=y2;} 49 } 50 printf("%.2lf ",cal(lx,ly)); 51 //传AB终值算答案 52 return 0; 53 }