随机梯度下降算法

1. 损失函数

在线性回归分析中，假设我们的线性回归模型为：

样本对应的正确数值为：

现在假设判别函数的系数都找出来了，那么通过判别函数G(x)，我们可以预测是样本x对的值为。那这个跟实际的y的差距有多大呢？这个时候我就出来一个损失函数：

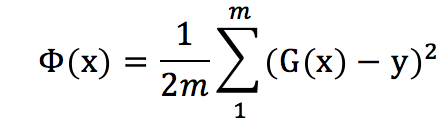
其实损失函数很容易理解，就是所有样本点的预测的值跟实际的值之间的差距的表达式而已。至于为什么有个1/2 分数，那只是为了后面求导的时候方便约掉那个平方而已。

2. 随机梯度下降算法

      其实梯度下降算法很好理解的。我们有了线性回归模型了，那么我们的目标就是要找出这些系数，而且这些系数怎么样也是最好的了。梯度下降算法就是来优化这个内容的，就是找出最佳的回归系数：

      而最佳的回归系数是不是要最小化，就是让损失函数的值越小越好。

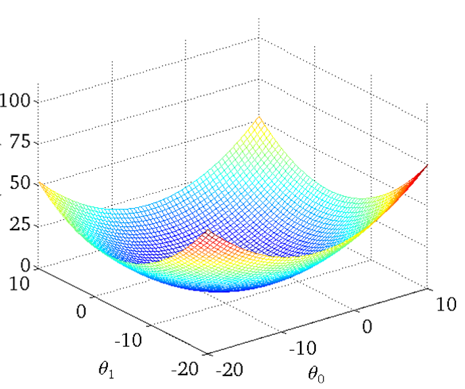
      当只有两个系数的时候，我们的损失函数就如上图一样。那么谷底就是一个最优解了。那么应该怎么来找到谷底呢？是不是当我们初始化之后，然后往谷底的方向慢慢来调节，让损失函数的值越来越小呢。对，就是这样的，那么怎么来确定这个方向呢？这是关键所在。这时候，我们就需要理解对一个函数求导的意义了。其实导数的意义很简单。

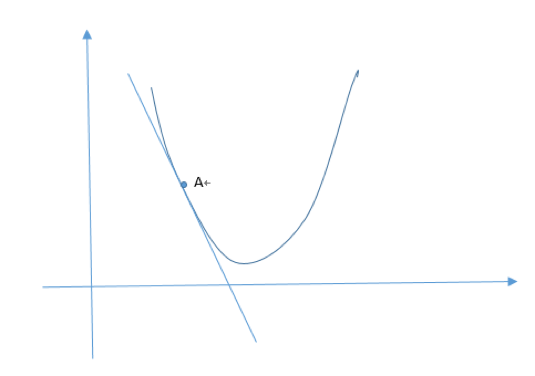
      在一个而平面上，如A点的导数就是该函数在点A的斜率。

如果我们的回归系数在优化的过程中，是按照下面的式子来优化的：

是步长，就是我们在优化时候，往损失函数最小化的方向走的一个长度。

      按照(1)式子，因为，即导数是负的，那么这个系数再减的话，就相当于加了，就是往导数的方向走，那么导数的值就越来越大，导数这条直线就越来越平。但导数这条直线平移x轴的时候，就是谷底了，也就是损失函数的最优解了。

     根据上面的坐标轴图，如果A点在右边也没关系，如果在右边，那么就为正数，就相当于减去一个值，同样也是往最小的方向走，导致的值越到越小，当导数这条直线平行x轴时候，就到谷底了，也就是到了最小的地方了。

     那么对所有的系数进行如下的操作，就能找到一个最优解了。

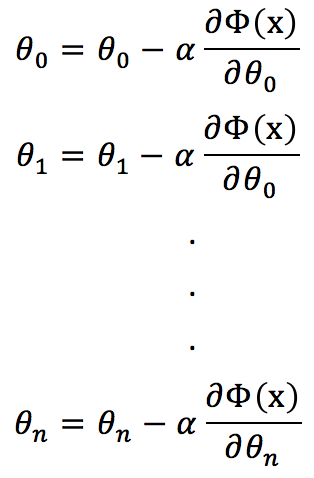
你也许有个问题，就是步长因为是认为指定的，它的取值会不会另损失函数不能到达谷底，只是在附近而已。这个是会的，所以有些算法就专门针对这个问题进行研究，比如当越接近谷底的时候步长越来越小等。