第三章：1.栈和队列 -- 栈的表示及实现

前言：

　　栈和队列 是两种重要的线性结构。从数据结构角度来看，栈和队列也是线性表，它的特殊性在于其操作是线性表的子集，是操作受限的线性表，因此可以称作限定性的数据结构。

　　（限定性：如、人为的规定线性表只能从表尾插入和删除结点数据元素，那么这样的线性表就是栈）

目录：

　　1、栈

　　2、栈的应用举例

　　3、栈与递归的实现

　　4、队列

　　5、离散事件模型

正文：

　　栈的定义

　　　　栈（stack） 如上所说，就是限定只能在表尾进行插入和删除的线性表。表尾 称为 栈顶（top）, 表头 称为 栈底 （bottom）,没有数据元素 称为 空栈

　　　　假设栈 S=(a1, a2, a3 ... an); 那么 a1 为栈底元素，an 为栈顶元素。因为栈的修改是按照 后进先出的原则进行，因此又称栈为 后进先出（last in first out）的线性表。可用下图表示：

　　　　　　

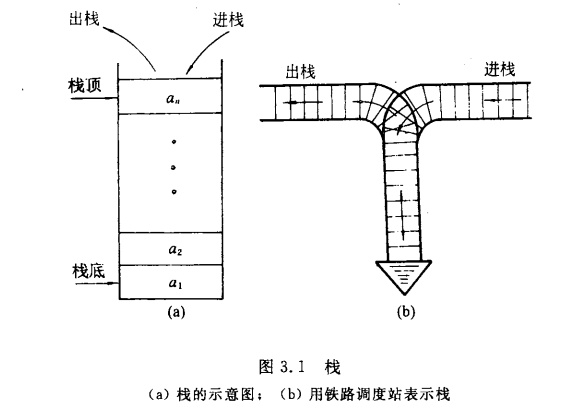
　　栈的表示和实现

　　　　栈和线性表一样也有两种表示形式

　　　　顺序栈，即栈的顺序存储结构是利用一组地址连续的存储单元依次存放栈底到栈顶的数据元素，同时附设 base 作为栈底指针，top 作为 栈顶指针。

　　　　　　一般来说，在初始化栈的时候不应该限定栈的最大容量。我们在此的做法是：先为栈分配一个基本容量，然后在应用的过程中，当栈的空间不够用的时候再逐段夸大。

　　　　　　因此需设定两个常量： STACK_INIT_SIZE（初始分配量） 和 STACKINCREMENT（分配增量）

　　　　　　元素和栈指针的关系图：

　　　　　　

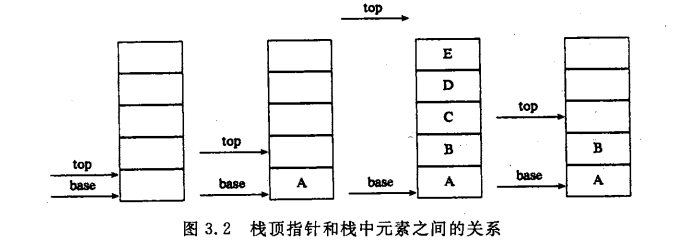
　　　　　　C语言中，讲顺序栈描述如下：

　　　　　　typedef struct {
    　　　　　　SElemType * base;
   　　　　　　 SElemType * top;
   　　　　　　 int stacksize;
　　　　　　}SqStack;

　　　　实现代码：

　　　　　　

#include<stdio.h>
#include<stdlib.h>

#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2

#define STACK_INIT_SIZE 100
#define STACKINCREMENT 10
//Status是函数的类型，其值是函数结果状态码
typedef int Status;
typedef int SElemType;

typedef struct {
    SElemType * base;
    SElemType * top;
    int stacksize;
}SqStack;

//构造空栈
Status InitStack(SqStack &S){
    S.base=(SElemType *)malloc(sizeof(SElemType)*STACK_INIT_SIZE);
    if(!S.base) exit(OVERFLOW);
    S.top=S.base;
    S.stacksize=STACK_INIT_SIZE;
    return OK;
}

//插入元素 （入栈）
Status Push(SqStack &S,SElemType e){
    if((S.top-S.base)==S.stacksize){                                        //空间不够，继续分配空间
        S.base=(SElemType *)realloc(S.base,(S.stacksize+STACKINCREMENT)*sizeof(SElemType));
        if(!S.base) exit(OVERFLOW);
        S.top=S.base+S.stacksize;
        S.stacksize+=STACKINCREMENT;
    }
    *S.top=e;
    S.top++;
    return OK;
}

//删除元素（出栈）
Status Pop(SqStack &S,SElemType &e){
    if(S.top!=S.base){
        e=*(--S.top);
    }else{
        return ERROR;
    }
    return OK;
}



void printAllValues(SqStack &S){
    SElemType * q=S.top;
    printf("top：%p
",q);
    while(q!=S.base){
        printf("地址：%p，",q-1);
        printf("值：%d
",*(q-1));
        q--;
    }
    printf("base：%p
",S.base);
}


void main(){
    SqStack S;
    if(InitStack(S)){
        printf("%s
","初始化空栈成功！");
    }
    
    printf("%s
","进行入栈操作Push:");
    Push(S,2);
    Push(S,5);
    Push(S,66);
    Push(S,31);
    printf("%s
","S:");
    printAllValues(S);

    printf("
%s
","出栈后：");
    SElemType e;
    Pop(S,e);
    printAllValues(S);
    printf("
出栈元素：%d
",e);
}

　　　　运行结果：

　　　　　　

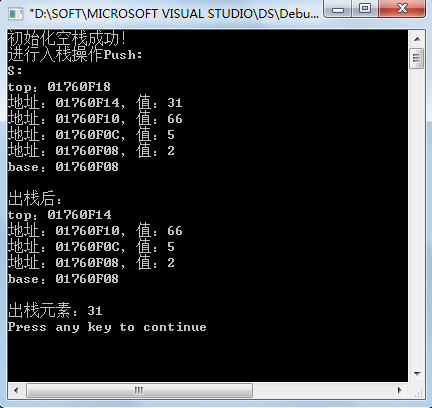
　　栈的链式表示：　　　　　　　　　　　　　　　

　　　　因为栈的操作是线性表操作的子集，所以链式栈的实现比较容易，在此也不予以实现来了。