Consider a N*N*N lattice. One corner is at (0,0,0) and the opposite one is at (N,N,N). How many lattice points are visible from corner at (0,0,0) ?
A point X is visible from point Y iff no other lattice point lies on the segment joining X and Y.
Input :
The first line contains the number of test cases T. The next T lines contain an interger N
Output :
Output T lines, one corresponding to each test case.
Sample Input :
3
1
2
5
Sample Output :
7
19
175
Constraints :
T <= 50
1 <= N <= 1000000
题意就是给你一个三维的地图,坐标为(0,0,0)∼(n,n,n),判断有多少个坐标与原点之间的连线不经过其他的点。
思路:统计答案的点分为三类
1.坐标轴上的点(1,0,0)(0,1,0)(0,0,1) 三个
2.xoy,xoz,xoy面上的点gcd(i,j)==1; 二维很简单
3.其他点 gcd(i,j,k)==1
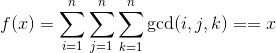
代码如下:
1 #include <bits/stdc++.h> 2 3 using namespace std; 4 typedef long long ll; 5 const int maxn = 1000000+50; 6 int p[maxn],mo[maxn],phi[maxn],cnt=0; 7 bool vis[maxn]; 8 void init() 9 { 10 mo[1]=1; 11 phi[1]=1; 12 for(int i=2;i<=maxn-10;i++){ 13 if(!vis[i]){ 14 mo[i]=-1; 15 phi[i]=i-1; 16 p[cnt++]=i; 17 } 18 for(int j=0;j<cnt&&(ll)i*p[j]<=maxn-10;j++){ 19 vis[i*p[j]]=true; 20 if(i%p[j]==0){ 21 mo[i*p[j]]=0; 22 phi[i*p[j]]=phi[i]*p[j]; 23 break; 24 } 25 mo[i*p[j]]=-mo[i]; 26 phi[i*p[j]]=phi[i]*(p[j]-1); 27 } 28 } 29 } 30 int n; 31 int main() 32 { 33 //freopen("de.txt","r",stdin); 34 init(); 35 int T; 36 scanf("%d",&T); 37 while (T--){ 38 scanf("%d",&n); 39 ll ans = 0; 40 for (int i=1;i<=n;++i){ 41 ans+=(ll)mo[i]*(n/i)*(n/i)*(n/i); 42 } 43 for (int i=1;i<=n;++i){ 44 ans+=(ll)mo[i]*(n/i)*(n/i)*3; 45 } 46 printf("%lld ",ans+3); 47 } 48 return 0; 49 }