题目描述
某国有(n)个城市,它们互相之间没有公路相通,因此交通十分不便。为解决这一“行路难”的问题,政府决定修建公路。修建公路的任务由各城市共同完成。
修建工程分若干轮完成。在每一轮中,每个城市选择一个与它最近的城市,申请修建通往该城市的公路。政府负责审批这些申请以决定是否同意修建。
政府审批的规则如下:
((1))如果两个或以上城市申请修建同一条公路,则让它们共同修建;
((2))如果三个或以上的城市申请修建的公路成环。如下图,(A)申请修建公路(AB),(B)申请修建公路(BC),(C)申请修建公路(CA)。则政府将否决其中最短的一条公路的修建申请;

((3))其他情况的申请一律同意。
一轮修建结束后,可能会有若干城市可以通过公路直接或间接相连。这些可以互相:连通的城市即组成“城市联盟”。在下一轮修建中,每个“城市联盟”将被看作一个城市,发挥一个城市的作用。
当所有城市被组合成一个“城市联盟”时,修建工程也就完成了。
你的任务是根据城市的分布和前面讲到的规则,计算出将要修建的公路总长度。
输入输出格式
输入格式:
第一行一个整数(n),表示城市的数量。((n≤5000))
以下(n)行,每行两个整数(x)和(y),表示一个城市的坐标。((-1000000≤x,y≤1000000))
输出格式:
一个实数,四舍五入保留两位小数,表示公路总长。(保证有惟一解)
输入输出样例
输入样例#1:
4
0 0
1 2
-1 2
0 4
输出样例#1:
6.47
说明
修建的公路如图所示: 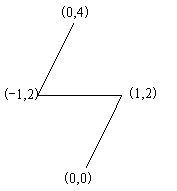
思路:第一眼,我们思路是对每两个点求出它们之间的距离,然后建边,跑(Kruskal),但是看了数据范围后放弃了,因为(m)太大,不能用(Kruskal),于是就用(prim),但是数组好像又开不下,那就干脆从(1)开始扩展,先(O(n))处理出(1)号点到其它所有点的距离,然后再跑(prim),因为保证一定有解,跑完之间输出答案就行了。
代码:
#include<cstdio>
#include<cstring>
#include<cmath>
#define maxn 5007
#define dl double
using namespace std;
int n,m,x[maxn],y[maxn];
dl dis[maxn],ans,minn,num;
bool vis[maxn];
inline dl jl(int i,int j) {
return sqrt((double)(x[i]-x[j])*(x[i]-x[j])+(double)(y[i]-y[j])*(y[i]-y[j]));
}
int main() {
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d%d",&x[i],&y[i]);
for(int i=2;i<=n;++i) dis[i]=jl(1,i);
dis[1]=0,vis[1]=1;
for(int i=1;i<n;++i) {
minn=1e9;
int k=0;
for(int j=1;j<=n;++j) if(!vis[j]&&minn>dis[j]) minn=dis[j],k=j;
vis[k]=1,ans+=minn;
for(int j=1;j<=n;++j) {
num=jl(k,j);
if(!vis[j]&&dis[j]>num) dis[j]=num;
}
}
printf("%0.2lf",ans);
return 0;
}