Problem Description
> The Death Star, known officially as the DS-1 Orbital Battle Station, also known as the Death Star I, the First Death Star, Project Stardust internally, and simply the Ultimate Weapon in early development stages, was a moon-sized, deep-space mobile battle station constructed by the Galactic Empire. Designed to fire a single planet-destroying superlaser powered by massive kyber crystals, it was the pet project of the Emperor, Darth Vader, and its eventual commander Grand Moff Wilhuff Tarkin to expound the military philosophy of the aptly named Tarkin Doctrine.
>
> — Wookieepedia
In the story of the Rogue One, the rebels risked their lives stolen the construction plan of the Death Star before it can cause catastrophic damage to the rebel base. According to the documents, the main weapon of the Death Star, the Superlaser, emits asymmetric energy in the battlefield that cause photons to annihilate and burns everything in a single shot.
You are assigned the task to estimate the damage of one shot of the Superlaser.
Assuming that the battlefield is an n×n grid. The energy field ignited by the Superlaser is asymmetric over the grid. For the cell at i-th row and j-th column, ⌈i/j⌉units of damage will be caused. Furthermore, due to the quantum effects, the energies in a cell cancel out if gcd(i,j)≠1 or i<j.
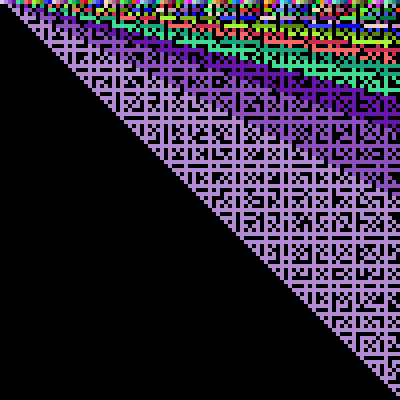
The figure below illustrates the damage caused to each cell for n=100. A cell in black indicates that this cell will not be damaged due to the quantum effects. Otherwise, different colors denote different units of damages.
Your should calculate the total damage to the battlefield. Formally, you should compute
where [(i,j)=1] evaluates to be 1 if gcd(i,j)=1, otherwise 0.
>
> — Wookieepedia
In the story of the Rogue One, the rebels risked their lives stolen the construction plan of the Death Star before it can cause catastrophic damage to the rebel base. According to the documents, the main weapon of the Death Star, the Superlaser, emits asymmetric energy in the battlefield that cause photons to annihilate and burns everything in a single shot.
You are assigned the task to estimate the damage of one shot of the Superlaser.
Assuming that the battlefield is an n×n grid. The energy field ignited by the Superlaser is asymmetric over the grid. For the cell at i-th row and j-th column, ⌈i/j⌉units of damage will be caused. Furthermore, due to the quantum effects, the energies in a cell cancel out if gcd(i,j)≠1 or i<j.
The figure below illustrates the damage caused to each cell for n=100. A cell in black indicates that this cell will not be damaged due to the quantum effects. Otherwise, different colors denote different units of damages.

Your should calculate the total damage to the battlefield. Formally, you should compute
f(n)=∑i=1n∑j=1i⌈ij⌉[(i,j)=1],
where [(i,j)=1] evaluates to be 1 if gcd(i,j)=1, otherwise 0.
Input
There are multiple test cases.Each line of the input, there is an integer n (1≤n≤106), as described in the problem. There are up to 10^4 test cases.
Output
For each test case, output one integer in one line denoting the total damage of the Superlaser, f(n) mod 109+7.
Sample Input
1
2
3
10
Sample Output
1
3
8
110
出题人是个星战狂魔前面不用看.
就是让你计算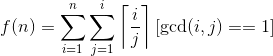
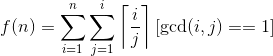
//这句话没用.... 套路的看第二个sigma的上界可以直接写成n,于是就变成了
根据Q神的思路我们令
那么
为什么呢?
我们在求g(n)的时候不要求gcd(i,j)==1,那么我们枚举gcd(i,j)=d,那么对于d,它肯定是i的因子即 d|i
对于每个d,j有可能有 种答案 即从 d,2*d,3*d... (i/d)*d 这
个数中选择与i互质的统计起来
而 跟
一定是互质的.而且
那么上面的对于每一个d统计的结果就是
那么枚举d后即
可以用前缀和求出来.
而且
代码如下:
1 #include <bits/stdc++.h> 2 3 using namespace std; 4 const int maxn = 1e6+10; 5 const int mod = 1e9+7; 6 int g[maxn]; 7 int n; 8 void init() 9 { 10 for (int i=1;i<=maxn-10;++i){ 11 g[i]++; 12 g[i+1]--; 13 for (int j=i,cnt=2;j+1<=maxn-10;j+=i,cnt++){ 14 g[j+1]+=cnt; 15 if (j+1+i<=maxn-10) g[j+1+i]-=cnt; 16 } 17 } 18 for (int i=1;i<=maxn-10;++i) 19 g[i]=(g[i]%mod+g[i-1]+mod)%mod; 20 21 22 for (int i=1;i<=maxn-10;++i){ 23 for (int j=i*2;j<=maxn-10;j+=i){ 24 g[j]=(g[j]-g[i]+mod)%mod; 25 } 26 } 27 for (int i=1;i<=maxn-10;++i) 28 g[i]=(g[i]+g[i-1])%mod; 29 } 30 int main() 31 { 32 init(); 33 while (~scanf("%d",&n)){ 34 printf("%d ",g[n]%mod); 35 } 36 return 0; 37 }