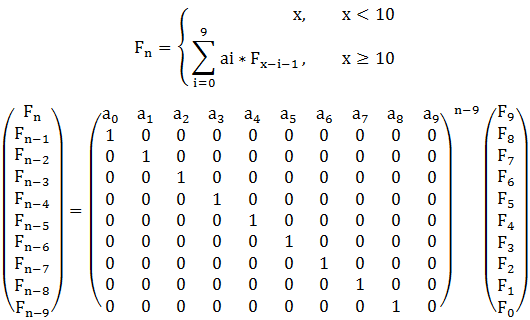hdu 1757 A Simple Math Problem （矩阵快速幂）

Description

Lele now is thinking about a simple function f(x).

If x < 10 f(x) = x.
If x >= 10 f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10);
And ai(0<=i<=9) can only be 0 or 1 .

Now, I will give a0 ~ a9 and two positive integers k and m ,and could you help Lele to caculate f(k)%m.

Input

The problem contains mutiple test cases.Please process to the end of file.
In each case, there will be two lines.
In the first line , there are two positive integers k and m. ( k<2*10^9 , m < 10^5 )
In the second line , there are ten integers represent a0 ~ a9.

Output

For each case, output f(k) % m in one line.

Sample Input

10 9999
1 1 1 1 1 1 1 1 1 1
20 500
1 0 1 0 1 0 1 0 1 0

Sample Output

45
104


这就算我写的第一道矩阵快速幂的题了！
矩阵快速幂的给我的感觉就是先找规律，YY出一个n*n的矩阵，矩阵左边写一列数，矩阵右边写一列数。让矩阵乘上右边那一列数等于左边的那列数。盗张图！！

然后......然后就没有然后了QWQ，输出答案就行了。
代码如下：

#include <bits/stdc++.h>

using namespace std;
const int N=10;
int k,m;
struct Matrix//用结构体来存矩阵
{
    long long int mat[N][N];//直接上long long int 别找事
}matrix;
void init()
{
    for (int i=0;i<N;++i)
    scanf("%lld",&matrix.mat[0][i]);
    for (int i=1;i<N;++i)
    {
        for (int j=0;j<N;++j)
        {
            if (i==j+1)
            matrix.mat[i][j]=1;
            else
            matrix.mat[i][j]=0;
        }
    }
}
Matrix operator * (Matrix a,Matrix b)//定义乘号
{
    Matrix c;
    for (int i=0;i<N;++i)
    {
        for (int j=0;j<N;++j)
        {
            c.mat[i][j]=0;//初始化值为0
            for (int k=0;k<N;++k)
            c.mat[i][j]+=a.mat[i][k]*b.mat[k][j];
            c.mat[i][j]%=m;//记得取模，否则就炸了
        }
    }
    return c;
}
Matrix Pow (int n)//定义快速幂函数
{
    Matrix t;
    if (n==1)
    return matrix;
    if (n&1)
    return matrix*Pow(n-1);
    else
    {
        Matrix temp=Pow(n>>1);
        return temp*temp;
    }
}
int main()
{
    //freopen("de.txt","r",stdin);
    while (~scanf("%d%d",&k,&m))
    {
        init();
        if (k<10)
        {
            printf("%lld
",matrix.mat[0][k]%m);
            continue;
        }
        Matrix temp=Pow(k-9);
        long long int ans=0;
        for (int i=0;i<N;++i)
        {
            ans += temp.mat[0][i]*(N-i-1);
            ans%=m;
        }
        printf("%lld
",ans);
    }
    return 0;
}