对于我这样一名脑残ACMer选手,这道题看了好久好久大概4天,终于知道怎样把它和“树状数组”联系到一块了。
树状数组是什么意思呢?用十个字归纳它:心里有数组,手中有前缀。
为什么要用树状数组?假设你要储存一段数字的前缀和,还要动态修改这些数字。怎么办?
通常的想法就是用数组a[]保存所有的数字,再用数组s[]保存每一位上的前缀和。
1 for(int i=1;i<=n;i++){ 2 3 s[i]=s[i-1]+a[i]; 4 5 }
这样有一个弊端,就是当你动态修改a[]数组中的数字的时候,维护s[]数组的代价太高了,最坏可达O(N),每修改一次都要O(N)的代价对于n=1000,000这样的的数据,显然修改十几次就要超时了。
那么这时候就可以用树状数组来存了,它的复杂度只有O(logN)。
也就是相当于把n二分的速度,非常快。
首先假设一个数组A[]和另一个保存其子串前缀和的数组C[],形状如下图:
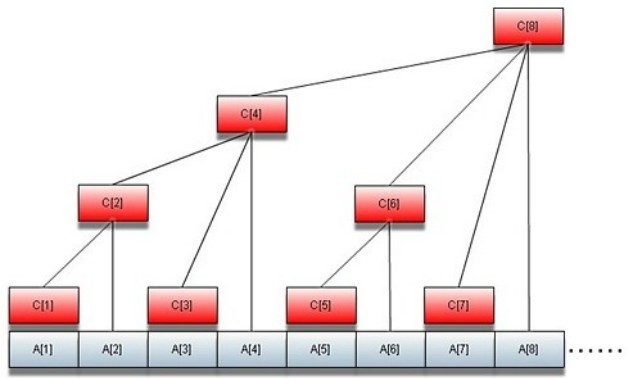
对于A[]数组,就是我所介绍的,心中的数组。
而C[]数组,就是手中的子串前缀和。
引入一个lowbit(x)的概念,lowbit(x)定义为x的二进制位最右边的1所对应的值,比如1表示1,10表示2,100表示4,这就是他们的值。lowbit只会为2^k(k>=0)。
令C[x]=A[x-lowbit(x)+1]+A[x-lowbit(x)+2]+...+A[x],那么每个C[x]都会对应一部分它的lowbit(x)范围内的A[i]。
假如我要求x的前缀和,只要先取出C[x],再取出C[x-lowbit(x)]也就是C[x]的左边界,令x=lowbit(x)也就是原来的C[x]的左边界的再左边一位,依次重复取C[x],直到x=0。
比如拿x=7做一个示范,我要求x=7的前缀和,也就是A[1]+A[2]+...+A[7],如下图:
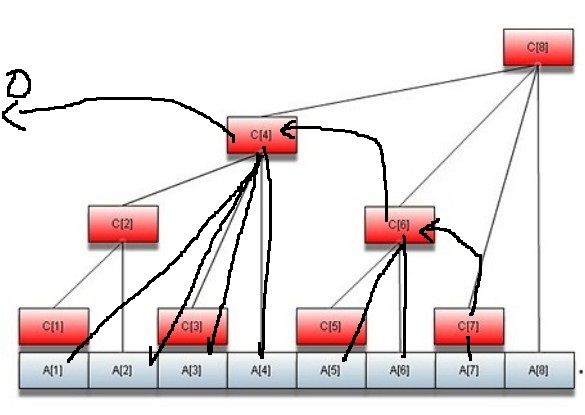
这样就求得了A[7]的前缀和。
实现:
1 int lowbit(int x) 2 { 3 return x&(-x); 4 } 5 int sum(int x) 6 { 7 int ret=0; 8 for(;x;x-=lowbit(x)) 9 ret+=C[x]; 10 return ret; 11 }
那当A[]某一位数据发生了变化,应该维护C[]的值,要注意A[]其实是你心里的数组,而C[]才是它的表现形式。
维护C[]就像是求有哪些C[]覆盖到了A[i],对于A[3]来打个比方,如下图所示:

每次向右上方“爬”,x=3开始,修改C[x],x加上自己的lowbit(x),此时x=4,再修改C[4],x加上自己的lowbit(x),此时x=8,直到x超出了C数组的上界。
实现:
void updata(int x,int d) { for(;x<=maxn;x+=lowbit(x)) C[x]+=d; }
现在把树形数组的概念运用到这道题里面来实践一下。
把运动员排成一排,对于其中任意一个位置i上的人来说,如果他作为裁判,则有这么两种可能:
1.左边的某人能力值低于他,右边高于他;
2.左边的某人能力值高于他,右边低于他。
记左边比他小的人数为l[i],右边比他小的人数为r[i],
那么左边比他大的人数为i-1-l[i],右边比他大的人数为n-i-r[i],
则i作为裁判就有l[i]*(n-i-r[i])+(i-1-l[i])*r[i];
求l[i]的方法呢,就是创一个hash数组,从a[1]扫到a[i-1],对hash[a[k]]++,判断hash[]中a[i]的前缀和,也就是l[i]的值了;
前缀和就是用树状数组保存和维护。
r[i]类似,只不过是逆序读取a[i]构造hash表。
实现:
1 #include <stdio.h> 2 #include <string.h> 3 const int maxn=100005; 4 int C[maxn]; 5 int lowbit(int x) 6 { 7 return x&(-x); 8 } 9 int sum(int x) 10 { 11 int ret=0; 12 for(;x;x-=lowbit(x)) 13 ret+=C[x]; 14 return ret; 15 } 16 void updata(int x) 17 { 18 for(;x<=maxn;x+=lowbit(x)) 19 C[x]++; 20 } 21 int a[maxn],cc[maxn],dd[maxn]; 22 int main() 23 { 24 int i,t,n; 25 long long ans; 26 scanf("%d",&t); 27 while(t--){ 28 scanf("%d",&n); 29 for(i=1;i<=n;i++) scanf("%d",&a[i]); 30 memset(C,0,sizeof(C)); 31 for(i=1;i<=n;i++){ 32 cc[i]=sum(a[i]); 33 updata(a[i]); 34 } 35 memset(C,0,sizeof(C)); 36 for(i=n;i;i--){ 37 dd[i]=sum(a[i]); 38 updata(a[i]); 39 } 40 ans=0; 41 for(i=1;i<=n;i++) 42 ans+=1LL*cc[i]*(n-i-dd[i])+1LL*(i-1-cc[i])*dd[i]; 43 printf("%lld ",ans); 44 } 45 return 0; 46 }