AC自动机板子

#include <queue>
#include <cstdlib>
#include <cmath>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn =  2*1e6+9;

int trie[maxn][26]; //字典树
int cntword[maxn];  //记录该单词出现次数
int fail[maxn];     //失败时的回溯指针


int cnt = 0;

void insertWords(string s){
    int root = 0;
    for(int i=0;i<s.size();i++){
        int next = s[i] - 'a';
        if(!trie[root][next])
            trie[root][next] = ++cnt;
        root = trie[root][next];
    }
    cntword[root]++;      //当前节点单词数+1
}
void getFail(){
    queue <int>q;
    for(int i=0;i<26;i++){      //将第二层所有出现了的字母扔进队列
        if(trie[0][i]){
            fail[trie[0][i]] = 0;
            q.push(trie[0][i]);
        }
    }

//fail[now]    ->当前节点now的失败指针指向的地方
//tire[now][i] -> 下一个字母为i+'a'的节点的下标为tire[now][i]
    while(!q.empty()){
        int now = q.front();
        q.pop();

        for(int i=0;i<26;i++){      //查询26个字母
            if(trie[now][i]){
                //如果有这个子节点为字母i+'a',则
//让这个节点的失败指针指向(((他父亲节点)的失败指针所指向的那个节点)的下一个节点)
                //有点绕,为了方便理解特意加了括号

                fail[trie[now][i]] = trie[fail[now]][i];
                q.push(trie[now][i]);
            }
            else//否则就让当前节点的这个子节点
                //指向当前节点fail指针的这个子节点
                trie[now][i] = trie[fail[now]][i];
        }
    }
}


int query(string s){
    int now = 0,ans = 0;
    for(int i=0;i<s.size();i++){    //遍历文本串
        now = trie[now][s[i]-'a'];  //从s[i]点开始寻找
        for(int j=now;j && cntword[j]!=-1;j=fail[j]){
            //一直向下寻找,直到匹配失败(失败指针指向根或者当前节点已找过).
            ans += cntword[j];
            cntword[j] = -1;    //将遍历国后的节点标记,防止重复计算
        }
    }
    return ans;
}

int main() {
    int n;
    string s;
    cin >> n;
    for(int i=0;i<n;i++){
        cin >> s ;
        insertWords(s);
    }
    fail[0] = 0;
    getFail();
    cin >> s ;
    cout << query(s) << endl;
    return 0;
}

 

 

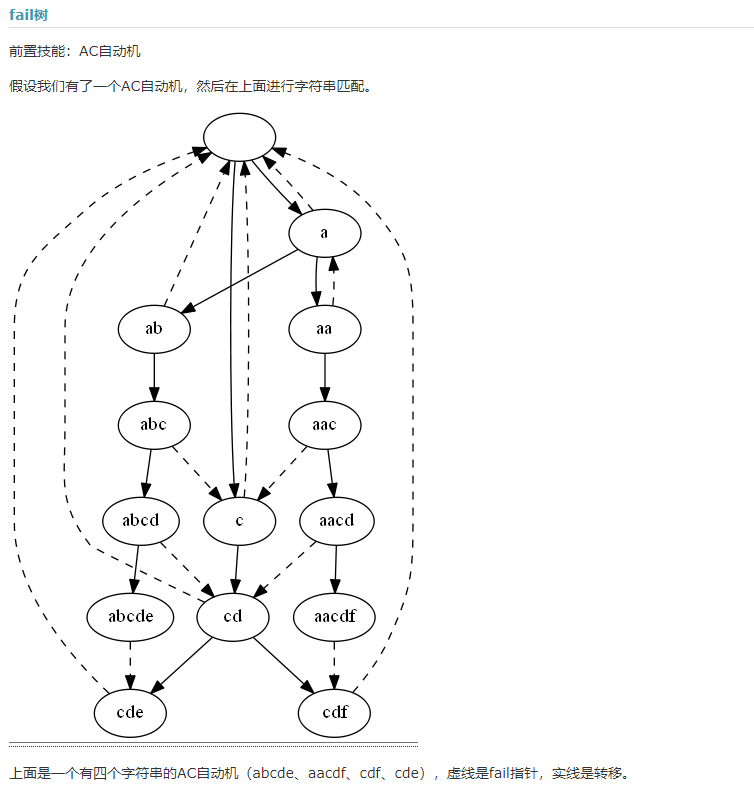
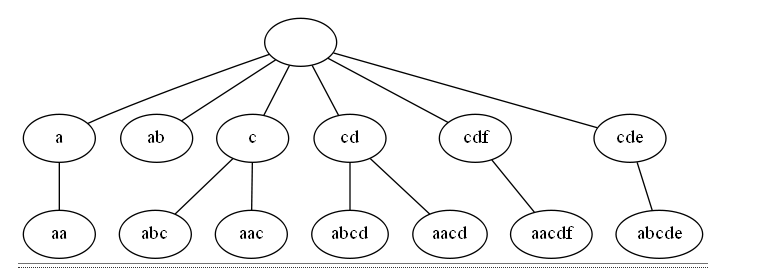
 这是fail树倒着连起来  发现从叶子一路走上去就是各个前缀的最大后缀一路连上去

所以就有了AC自动机fail树上dfs序建立可持久化线段树这个神奇的东西了

转自 ：https://blog.csdn.net/bestsort/article/details/82947639

转自 ：https://www.cnblogs.com/zzqsblog/p/6227545.html

侵权删

再就是这个复杂度 trie树复杂度肯定是所有小串加起来的长度

然后建fail指针是这个长度*26；

然后查询这个  其实就是 fail指针一路跑下去，暴力找每个前缀的最大后缀 然后套娃找最大后缀的最大后缀，然后他说这样复杂度是文本串的长度，。至今没搞懂 可能是fail太强了